Вопросам коррозии металлов посвящено огромное количество работ, из которых отметим лишь работы [1, 9–11], в которых приводится обширная библиография. Несмотря на это работы в области теории коррозии продолжают расти с ростом различных типов конструкционных металлических материалов, применяемых в различных областях промышленного производства.
В самом общем случае коррозию металла можно представить как зарождение и рост новой фазы (окисленного металла). Критический зародыш новой фазы образуется последовательно в серии случайных актов присоединения и отрыва атомов (молекул) друг от друга. Поэтому зародышеобразование – случайный процесс во времени и пространстве. Это предопределяет вероятностный характер параметров, которые описывают кинетику образования зародышей в процессе коррозии или роста кристалла [11].
Марковские процессы и кинетика образования зародышей новой фазы
Количественное описание случайного процесса дается его функцией распределения, удовлетворяющей кинетическому уравнению. В общем случае кинетическое уравнение является сложным интегро-дифференциальным уравнением, решить которое невозможно. Однако, если рассматривать случайный процесс как марковский, то кинетическое уравнение переходит в дифференциальное, которое имеет более простой вид [10].
В частном случае пуассоновского процесса гибели и размножения с конечным числом состояний получается система дифференциальных уравнений [5–6]:
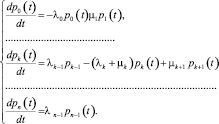(1)
Здесь λ0 – вероятность перехода системы из состояния E0 в E1 и т.д.; μ1 – вероятность перехода из состояния E1 в E0 и т.д. Вероятность перехода из En в En–1 полагается равной нулю (μn = 0), т.е. состояние En для такой системы – поглощающее; pi(t) – вероятность нахождения системы в состоянии Ei. Система уравнений (1) является системой уравнений Колмогорова [3]. Общее решение настолько громоздко, что не позволяет провести анализ даже численными методами.
Приведенный выше пример показывает, что большинство исследователей идет по пути решения уравнений диффузионного типа, математическая теория которых разработана достаточно полно и которые описывают процесс случайных (броуновских) блужданий, а также теории надежности, порядковых статистик, массового обслуживания и ряд других.
К числу основных кинетических уравнений, вытекающих из дифференциальных уравнений Колмогорова, для случайных марковских процессов относятся уравнения Смолуховского – Чепмена и Фоккера – Планка. В случае многомерного вектора состояния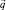 
, уравнение Фоккера – Планка имеет вид [9]
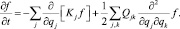(2)
Получить решение уравнения (2) в явном виде удается лишь в частных случаях, например, если величина K линейна по переменным q, а величина Qjk не зависит от q. Уравнение (2) имеет важную роль в нестационарной теории замедления нейтронов, однако его линеаризация приводит к тому, что его решение сводится к отысканию соответствующей функции Грина при различных граничных условиях.
Для решения стохастических дифференциальных уравнений диффузионного типа, к которым также относятся уравнения (1) и (2), развито несколько подходов, из которых необходимо отметить подходы Ито [4] и Стратоновича [7]. Решая записанные для процесса Маркова y(t) стохастические уравнения типа Ланжевена, можно находить соответствующие ему нестационарные или стационарные моменты и корреляторы, одновременные или многовременные стохастические уравнения Ито [7]:
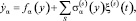(3)
где ξ(s)(t) – дельта-коррелированные по времени случайные функции, имеют недостатком то, что с входящими в него выражениями типа σ(y)ξ(t) при различных выкладках нельзя обращаться по обычным правилам, пригодным для гладких функций. Это обстоятельство неудобно с практической точки зрения.
Из сказанного выше отметим следующее:
– формальный вероятностный характер описания процесса новой фазы как случайного марковского стационарного или нестационарного процесса Пуассона требует более строгого обоснования, поскольку ряд предположений (отсутствие последействия, ординарность и др.) не вытекает из физической картины явления коррозии;
– так как экспериментально наблюдаемыми являются (как и в квантовой теории) не сами функции распределения, а их моменты и корреляторы, то целесообразно проведение анализа статистических закономерностей начальной стадии коррозии
Статистическая модель образования коррозионного пятна
Наиболее распространенным случаем коррозии металла является его взаимодействие с молекулами кислорода. Очевидно, что это взаимодействие начинается со «слабых» мест поверхности металла или с его дефектами. Мы изложим нашу модель образования коррозионного пятна с позиции статистической физики.
Рассмотрим поверхность металла с числом дефектов m. Пусть расстояние между дефектами одинаково и равно R. Опишем вокруг каждого дефекта 0 окружность радиусом R. Пусть плотность числа дефектов в этой окружности равна n0, тогда вероятность W0(r) того, что ближайшая частица кислорода попадет на расстояние r от частицы 0, нетрудно получить на основе статистической физики и она равна
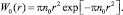(3)
Вероятность нахождения N0 частиц кислорода в зоне дефекта 0 радиусом r равна, очевидно,
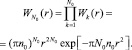(4)
Вероятность (4) определим, с другой стороны, как отношение числа частиц N0 в зоне дефекта к общему числу частиц в выделенной окружности – Q0:
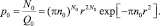(5)
Для системы из m дефектов имеем
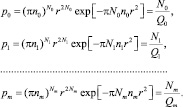(6)
Для всего металла с числом дефектов 0, 1, 2, …, m имеем
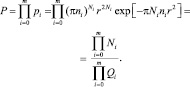(7)
Cистема уравнений (6) и (7) представляет собой систему трансцендентных уравнений, решить которую можно только приближенными или численными методами.
В связи с этим можно сделать численную оценку, основываясь на реальной ситуации и уравнении (1) системы (6):
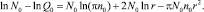
Соответствующая оценка дает, что первый член левой части уравнения и первые два члена правой части – пренебрежимо малы. В результате получим
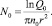(8)
Учитывая, что πr2 = S – площади коррозионного пятна и n0N0 = const, из (8) имеем
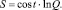(9)
Последнее выражение показывает логарифмическую зависимость площади коррозионного пятна от «дефектности» поверхности металла.
Учет энергии коррозионного процесса
Вероятность (4) можно определить, с другой стороны, и как отношение энергии связи молекулы кислорода Е0 с атомом металла к общей энергии образования коррозионного пятна Еобщ. Учитывая, что [1]
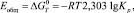(10)
где Kp – константа химического равновесия, проводя, аналогичные приведенным выше вычисления, для площади коррозионного пятна, получим
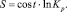(11)
Заключение
Несмотря на простоту формул (9) и (11) они могут быть полезными для исследования процессов коррозии любых конструкционных материалов, поскольку включают в себя легко определяемые в эксперименте параметры.
Работа выполнена по программе МОН РК 055 «Научная и/или научно-техническая деятельность», подпрограмма 101 «Грантовое финансирование научных исследований».
Рецензенты:
Портнов В.С., д.т.н., профессор, начальник УПО, Карагандинский государственный технический университет, г. Караганда;
Жакатаев Т.А., д.т.н., старший преподаватель кафедры ММ и Н, Карагандинский государственный технический университет, г. Караганда.
Работа поступила в редакцию 10.04.2015.
Библиографическая ссылка
Платонова Е.C., Бучинскас В., Юров В.М. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ОБРАЗОВАНИЯ КОРРОЗИОННОГО ПЯТНА НА МЕТАЛЛЕ // Фундаментальные исследования. – 2015. – № 2-14. – С. 3048-3051;URL: https://fundamental-research.ru/ru/article/view?id=37688 (дата обращения: 19.04.2024).