Процесс разработки газовых и нефтяных месторождений в шельфе океанов связан с непрерывным увеличением объемов потребляемых энергоресурсов, а также с огромными запасами океанических залежей нефти и газа. Разработка нефтяных и газовых месторождений в шельфе сопровождается техногенными авариями, вызванными повреждением скважин, что приводит к выбросу в океан нефти и газа.
Исследователями предлагается множество способов устранения последствий утечки углеводородов из скважины, например при аварии в Мексиканском заливе в 2010 г. [4] было предложено залить скважину бетоном или пробурить сопутствующие скважины. Также была предпринята попытка установки купола непосредственно над местом утечки с целью накопления внутри купола нефти и газа, но из-за накопления внутри купола гидратов эта конструкция приобрела положительную плавучесть и ее не смогли зафиксировать. Несмотря на это, технология устранения аварии под водой, основанная на использовании конструкции купола, остается привлекательной для инженеров и исследователей.
В данной работе представлена математическая модель процесса установки и работы купола-сепаратора [2], который опускается с поверхности океана над местом утечки углеводородов из скважины. Купол-сепаратор предназначен для немедленного монтажа непосредственно над местом утечки нефти с последующей эвакуацией нефти для безопасного хранения и газа для растворения в морской воде или утилизации. При достижении дна океана купол устанавливается непосредственно над местом утечки так, что вытекающие нефть и газ скапливаются внутри купола, а затем откачиваются через трубки в танкер, который находится на поверхности океана. На рис.1 приводится схема монтажа купола-сепаратора.
Физическая постановка задачи
Пусть на дне океана имеется осесимметричный источник (радиуса R) утечки углеводородной смеси (нефть и газ) c известным объемным дебитом нефти Qo, и газа Qg и температурой Te. Известны также теплофизические параметры окружающей среды и вытекающей смеси. Согласно предлагаемой технологии устранения аварий к месту утечки смеси опускается купол из мягкой полиуретановой оболочки и устанавливается строго над источником на высоте h0 от дна.
Процесс установки купола происходит в несколько этапов (рис. 1). С поверхности океана, непосредственно над местом аварии (фрагмент a) опускается купол в собранном виде. На некоторой высоте h0 от дна океана купол раскрывается и внутрь купола через открытую нижнюю часть устремляется струя углеводородов (фрагмент b).
На фрагменте c показан момент, когда купол зафиксирован на дне океана с помощью специальных фиксаторов, снизу внутрь купола поступает струя из источника и свободно покидает пределы купола через верхнюю часть, так как крышка купола не закрыта. Отметим, что по мере распространения струи в океане происходит захват окружающей холодной воды струей [5]. С увеличением координаты z струя расширяется [1, 4, 5]. За счет холодной воды, приходящей в струю, температура струи опускается до температуры окружающей среды. При большом давлении, когда температура струи становится ниже температуры гидратообразования, возможно образование газовых гидратов на поверхности пузырьков газа, которые продолжают двигаться вместе со струей. Затем верхняя часть купола закрывается, и смесь углеводородов начинает скапливаться внутри купола.
Будем полагать, что размеры купола достаточно большие и многофазная струя по мере поступления естественным образом сепарируется, а с течением времени внутри купола будет происходить расслоение флюидов. Начало расчета связано с моментом, когда верхняя часть купола закрывается и начинается происходить накопление углеводородной смеси внутри купола. В модели предположим, что купол установлен на такой высоте от скважины, что весь газ полностью успел превратиться в гидрат. Таким образом, внутри купола образуются области, насыщенные гидратом и нефтью. На начальном этапе рассматриваем только накопление углеводородов внутри купола и принимаем, что откачка нефти через трубку 4 (рис. 2) не происходит.
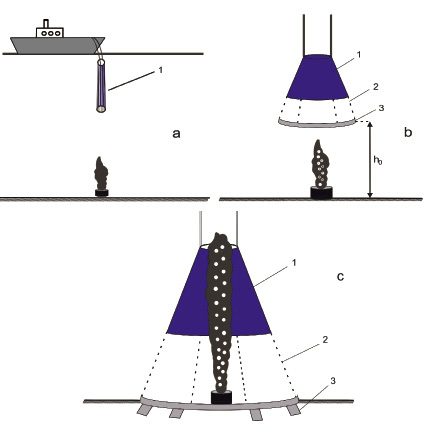
Рис. 1. Процесс установки купола-сепаратора: 1 – купол-сепаратор; 2 – тросы; 3 – фиксаторы
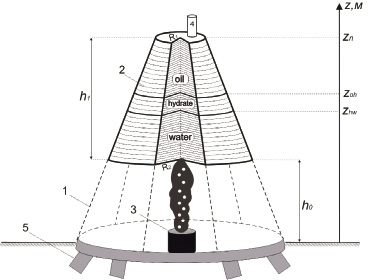
Рис. 2. Принципиальная схема купола-сепаратора: 1 – тросы; 2 – оболочка купола; 3 – скважина, через которую поступают нефть и газ; 4 – трубка для откачки нефти; 5 – фиксаторы
Введем координатную ось OZ (рис. 2). Будем полагать, что нефть и гидрат расслаиваются и накапливаются в области под куполом. Полагается, что нефть и гидрат расслаиваются под куполом и слои нефти и гидрата распределяются, как на рис. 2. Таким образом, нефть накапливается на участке zoh < z < zn, гидрат на участке zhw < z < zoh. Здесь zoh – координата раздела слоев нефти и гидрата; zhw – координата раздела гидрата и воды; ho, hh – толщины слоев нефти и гидрата. Кроме того, будем полагать, что газовый гидрат образуется в виде пены, которая не препятствует движению флюидов внутри купола.
Основные уравнения
Законы сохранения для масс для компонент струи, проникающей в купол, можно представить в следующем виде:
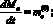
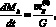(1)
здесь Mj – масса j-го компонента смеси в куполе;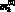 
– начальный массовый расход k-го компонента, нижние индексы o, g, h относятся соответственно к нефти (oil), газу (gas) и гидрату (hydrate).
Для определения средней температуры слоя нефти воспользуемся законом сохранения энергии. Запишем законы сохранения для слоя нефти:
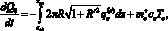(2)
здесь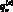 
– поток тепла от фазы нефти в окружающую воду через боковую стенку купола, Te – температура поступающей нефти из струи. Температура Te определяется для каждого значения z согласно [5].
Для определения теплового потока между нефтью и водой через стенку купола используем [3]:
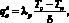
здесь λp – коэффициент теплопроводности полиуретана; To – температура нефти; Tw – температура воды; δ – толщина оболочки купола.
Результаты расчетов
Задача решалась при следующих параметрах: температура окружающей среды Tw = 277 K, температура вытекающей смеси Te = 353 K, co = 1670 Дж/(кг∙К), cw = 4200 Дж/(кг∙К), λo = 0,12 Вт/(м∙К), λw = 0,55 Вт/(м∙К), λp = 0,25 Вт/(м∙К), δ = 0,005 м. Параметры купола полагались равными: радиус скважины R0 = 0,85 м, радиус верхнего основания купола R1 = 3 м, радиус нижнего основания R1 = 26 м, высота купола h1 = 14 м, высота установки купола h0 = 10 м.
На рис. 3 представлена зависимость толщины каждой из фаз от времени. Заметим, что толщины фазы нефти (линия 1) и гидрата (линия 2) с течением времени растут, что связано с приходом углеводородов в купол из скважины. В каждый момент времени поступает одинаковое количество нефти и газа в предположении, что весь газ и вся нефть полностью попадают в купол. Весь поступающий газ идет на образование гидрата.
На рис. 4 изображены координаты раздела слоев нефти и гидрата, гидрата и воды. С учетом того, что купол установлен на высоте H = 35 м, видим, что координата каждой из фаз с течением времени убывает.
Время полного заполнения купола гидратом и нефтью составляет 12,5 часов.
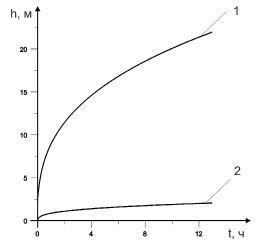
Рис. 3. График зависимости толщины j-го слоя от времени: 1 – ho(t); 2 – hh(t)
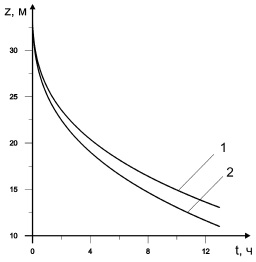
Рис. 4. Зависимость координаты z от времени: 1 – zoh(t); 2 – zhw(t)
Выводы
В работе предложена модель устройства, предназначенная для быстрого монтажа непосредственно над местом истечения в случае возникновения аварийной ситуации. Накопление углеводородов, поступающих из скважины, рассмотрено в предположении, что весь поступающий из скважины газ превращается в гидрат. Слои гидрата и нефти располагаются внутри купола согласно их плотностям: наверху нефть, снизу гидрат. При этом слой гидрата достаточно рыхлый, вследствие чего нефть может проходить через слой гидрата и накапливаться наверху. В результате моделирования получены зависимости толщин слоев нефти и гидрата от времени, а также динамика изменения координат раздела фаз нефть – гидрат и гидрат – вода.
Работа поддержана грантом СФ БашГУ В15-12.
Рецензенты:
Гималтдинов И.К., д.ф.-м.н., профессор, заведующий кафедрой «Прикладная информатика и программирование», Стерлитамакский филиал, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак;
Биккулова Н.Н., д.ф.-м.н., профессор кафедры «Общая физика», Стерлитамакский филиал, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.
Библиографическая ссылка
Кильдибаева С.Р. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НАПОЛНЕНИЯ КУПОЛА-СЕПАРАТОРА НЕФТЬЮ И ГИДРАТОМ // Фундаментальные исследования. – 2015. – № 7-3. – С. 535-539;URL: https://fundamental-research.ru/ru/article/view?id=38774 (дата обращения: 18.04.2024).