Рассматривая технические системы в процессе проектирования и эксплуатации, используя при этом критерии надежности, обращаются к рассмотрению структур, то есть к анализу структурной надежности. К системам с явно выраженными структурными связями относят электрические сети, трубопроводные системы, компьютерные сети и др. С позиции сохранения высокого уровня надежности таких систем пользуются общепринятыми методами расчета структурной надежности, например методами полного перебора состояний, дерева отказов, минимальных путей и сечений и другими. Фактически все они построены с использованием вероятностей безотказной работы pi и отказа qi элемента i системы. Применяя данные методы (при определенных условиях), можно выбирать структуру из рассматриваемого многообразия, удовлетворяющую требования по надежности.
Со структурной надежностью связывают такую составляющую состояния системы, как неопределенность информации, так как её количество обусловлено наличием связей и элементов системы, то есть топологией. Теория надежности может соприкасаться с теорией информации в плане определения её количества, необходимого для практики эксплуатации и проектирования. Например, согласно принципу К. Шеннона, информация – мера или количество неопределённости (информационной энтропии), связанное с результатом выбора из возможных альтернатив. Имея количество информации для той или иной структуры, можно судить об уровне содержащейся в ней неопределенности. Поэтому применение методов определения количества энтропии для структур технических систем может быть полезным с точки зрения оценки структурной надежности с позиции теории информации.
Далее предложим к рассмотрению математический метод перебора состояний, позволяющий определять количество информационной энтропии для различных структур технической системы.
Показатели структуры системы
Среди показателей выделяют вероятности безотказной работы и отказа элемента системы. Мера неопределенности информации непосредственно опирается на данные показатели. Для их определения строится (например, согласно [2, 3, 5]) статистический ансамбль. Используя его, определяют собственное значение информации I = log2N, N – количество всевозможных состояний элементов. Величина I задана рядом распределения, представляющего собой совокупность всех возможных отрицательных значений собственных (частных) информаций Ii и соответствующих им вероятностей pi [3]. Собственная информация является исходной для определения информационной (статистической) энтропии по Шеннону:
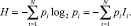 (1)
(1)
Выражение (1) выполнимо при условии
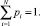
Вероятность, стоящая в (1) перед логарифмом, связывает информацию с энтропией и накладывает свой отпечаток на конечный результат. Дело в том, что в большинстве методов определения количества энтропии данная вероятность служит для усреднения количества энтропии. С позиции анализа структурной надежности, когда, с одной стороны, статистические характеристики неустойчивы, а с другой – события приходится рассматривать как совместные, усреднение может способствовать росту погрешности. Поэтому вопрос о том, какую величину вероятности поставить перед логарифмом энтропии Шеннона, тема для отдельных научных изысканий. Поэтому далее положим в основу классическое выражение (1), ограничившись предположением об усреднении энтропии.
Статистические характеристики структурной надежности, как было отмечено выше, учитывают вероятное появление противоположных событий, принадлежащих одному и тому же элементу системы. Наличие противоположных состояний и предположение о их независимости указывает на необходимость разделения в процессе расчетов значений энтропий по качественному признаку. В оценках структурной надежности качественный признак – «работа-отказ», поэтому процесс определения энтропии должен идти отдельно по каждому из противоположных состояний, поскольку при их слиянии утрачивается смысл оценки уровня надежности через меру информации [1].
Далее предложим к рассмотрению метод определения энтропии путем перебора состояний структуры с учетом качественного признака.
Определение энтропии методом перебора состояний элементов структуры
Вся совокупность состояний объекта складывается из потоков противоположных состояний,
N = Np + Nq,
где Np и Nq – количество состояний, относящихся к работе и отказу системы соответственно.
Определение энтропии для каждого из двух противоположных (непересекающихся) множеств состояний элементов зависит, с одной стороны, от числа элементов, состояния которых рассматриваются как независимые, с другой – от топологии структуры.
Рассмотрим вначале определение суммарной энтропии, когда для n элементов работоспособное и неработоспособное состояния независимы, а сумма их совместных комбинаций N = 2n – есть суммарная вероятность, равная единице. Например, для 2 элементов с вероятностями pi + qi = 1, N = 22 = 4, имеем комбинацию
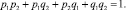 (2)
(2)
Согласно (1) и с учетом сумм независимых совместных событий по (2), суммарная энтропия двух независимых элементов:
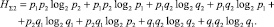 (3)
(3)
Выражение (3), с учетом энтропий противоположных событий 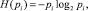
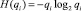 можно переписать в ином виде:
можно переписать в ином виде:
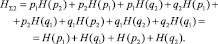 (4)
(4)
Исходя из (4), суммарная энтропия системы в общем виде:
HΣ = HΣ(p) + HΣ(q). (5)
Перейдем к рассмотрению определения энтропии с учетом топологии структур. Для этого используем метод перебора состояний. Он основан на выделении групп состояний, в виде набора элементов структуры, которые визуально отражают состояние всей структуры от источника до приемника информации: для работоспособного состояния – группа содержит сквозную связь или связи источника с приемником; для неработоспособного – связь или связи отсутствуют.
Условие о независимости состояний позволяет формировать группы через произведение вероятностей нахождения элементов в соответствующих состояниях p и q. Так, при числе групп состояний, равном Np, энтропия работоспособного состояния системы определится из выражения
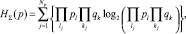 (6)
(6)
где Np – общее число работоспособных состояний, в каждом j-м из которых число исправных элементов равно lj, а вышедших из строя – kj.
Аналогично формируются группы событий неработоспособного состояния системы Nq для определения энтропии:
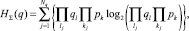 (7)
(7)
где Nq – общее число неработоспособных состояний, в каждом j-м из которых число неисправных элементов равно lj, а исправных – kj
Выражения (6) и (7) справедливы при условии
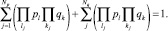 (8)
(8)
Величину HΣ(q) можно определить не только по выражению (7), но и в более простом виде, избегая формирования неработоспособных групп:
HΣ(q) = HΣ – HΣ(p). (9)
Расчет выполняется в три этапа:
● выявление множества возможных состояний;
● составление математических выражений по каждому из состояний;
● расчет информации с разделением по качественному признаку.
Пример
Определить количество информационной энтропии для мостиковой структуры, представленной на рисунке. Значения вероятностей: pi = 0,9; qi = 1 – pi = 0,1.
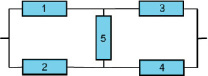
Мостиковая структура (схема)
Предварительно составляется таблица состояний с их разделением на два непересекающихся множества, отвечающих работоспособному и неработоспособному состояниям всей структуры. Каждое из этих состояний характеризуется набором элементов в рабочем (с указанием 1) и отказавшем (с указанием 0) состояниях (таблица). Предположение о независимости функционирования элементов системы позволяет сформировать комбинации состояний (представленных в таблице), вероятность которых определяется произведением вероятностей состояний элементов.
Значения из таблицы позволяют определить суммарное количество энтропии работоспособного состояния по выражению (6), HΣ(p) = –2,1687. Аналогично достраивается таблица для определения по (7), HΣ(q) = –0,1763. Суммарная энтропия состояний
HΣ5 = HΣ(p) + HΣ(q) = –2,345.
Из представленного примера видно: энтропия работоспособных состояний гораздо выше энтропии неработоспособных состояний, что свидетельствует о высокой структурной надежности системы.
У предлагаемого метода имеются недостатки: «проклятие» размерности (из примера видно, что даже при сравнительно простой структуре применение метода перебора состояний сопряжено с громоздкими выкладками) и необходимость учета всех состояний (или по крайней мере, относящихся к одному из качественных состояний).
Данные о состояниях элементов мостиковой структуры
|
Номер состояния |
Состояние элементов |
Вероятность состояний |
Выражения для определения энтропии Np |
Количество энтропии, бит |
||||
|
1 |
2 |
3 |
4 |
5 |
||||
|
1 |
1 |
1 |
1 |
1 |
1 |
p1p2p3p4p5 |
p1p2p3p4p5log2(p1p2p3p4p5) |
–0,4488 |
|
2 |
0 |
1 |
1 |
1 |
1 |
p2p3p4p5q1 |
q1p2p3p4p5log2(q1p2p3p4p5) |
–0,2578 |
|
3 |
1 |
0 |
1 |
1 |
1 |
p1p3p4p5q2 |
p1q2p3p4p5log2(p1q2p3p4p5) |
–0,2578 |
|
4 |
1 |
1 |
0 |
1 |
1 |
p1p2p4p5q3 |
p1p2q3p4p5log2(p1p2q3p4p5) |
–0,2578 |
|
5 |
1 |
1 |
1 |
0 |
1 |
p1p2p3p5q4 |
p1p2p3q4p5log2(p1p2p3q4p5) |
–0,2578 |
|
6 |
1 |
1 |
1 |
1 |
0 |
p1p2p3p4q5 |
p1p2p3p4q5log2(p1p2p3p4q5) |
–0,2578 |
|
7 |
0 |
1 |
0 |
1 |
1 |
p2p4p5q1q3 |
q1p2q3p4p5log2(q1p2q3p4p5) |
–0,0518 |
|
8 |
0 |
1 |
1 |
0 |
1 |
p2p3p5q1q4 |
q1p2p3q4p5log2(q1p2p3q4p5) |
–0,0518 |
|
9 |
0 |
1 |
1 |
1 |
0 |
p2p3p4q1q5 |
q1p2p3p4q5log2(q1p2p3p4q5) |
–0,0518 |
|
10 |
1 |
0 |
0 |
1 |
1 |
p1p4p5q2q3 |
p1q2q3p4p5log2(p1q2q3p4p5) |
–0,0518 |
|
11 |
1 |
0 |
1 |
0 |
1 |
p1p3p5q2q4 |
p1q2p3q4p5log2(p1q2p3q4p5) |
–0,0518 |
|
12 |
1 |
0 |
1 |
1 |
0 |
p1p3p4q2q5 |
p1q2p3p4q5log2(p1q2p3p4q5) |
–0,0518 |
|
13 |
1 |
1 |
0 |
1 |
0 |
p1p2p4q3q5 |
p1p2q3p4q5log2(p1p2q3p4q5) |
–0,0518 |
|
14 |
1 |
1 |
1 |
0 |
0 |
p1p2p3q4q5 |
p1p2p3q4q5log2(p1p2p3q4q5) |
–0,0518 |
|
15 |
0 |
1 |
0 |
1 |
0 |
p2p4q1q3q5 |
q1p2q3p4q5log2(q1p2q3p4q5) |
–0,0083 |
|
16 |
1 |
0 |
1 |
0 |
0 |
p1p3q2q4q5 |
p1q2p3q4q5log2(p1q2p3q4q5) |
–0,0083 |
Примечание. В таблице представлены только работоспособные состояния элементов.
Заключение
Основное назначение данного метода – оценка качественного и количественного содержания информации, полученная на основе перебора состояний элементов структуры. Интеграция данного метода в среду оценки структурной надежности через меру неопределенности информации позволяет определить усредненное по параметрам состояние технической системы. С помощью полученных математических выражений можно рассчитывать количество информации отдельно для работоспособного и неработоспособного состояний системы.
Рассматривая различные варианты структур системы, используя предлагаемый метод, можно выбрать более надежную структуру с позиции наличия в ней определенного количества меры неопределенности информации.
Метод справедлив в случае нормировки количества энтропии согласно [4] и подлежит формализации, что позволяет реализовать его через программную среду.
Работа выполнена при поддержке гранта РФФИ №15-08-01473.
Рецензенты:
Гафнер Ю.Я., д.ф.-м.н., зав. кафедрой общей и экспериментальной физики, Хакасский государственный университет им. Н.Ф. Катанова, г. Абакан;
Кочетков В.П., д.т.н., профессор кафедры электроэнергетики, Хакасский технический институт (филиал), Сибирский федеральный университет, г. Абакан.
Библиографическая ссылка
Дулесов А.С., Кондрат Н.Н. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИОННОЙ ЭНТРОПИИ В СТРУКТУРЕ ТЕХНИЧЕСКОЙ СИСТЕМЫ МЕТОДОМ ПЕРЕБОРА СОСТОЯНИЙ // Фундаментальные исследования. – 2015. – № 7-4. – С. 745-748;URL: https://fundamental-research.ru/ru/article/view?id=38813 (дата обращения: 19.04.2024).



