Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Желдашева А.О. 1 Лесев В.Н. 1

---

1 Кабардино-Балкарский государственный университет им. Х.М. Бербекова

В работе сформулирована и исследована краевая задача для смешанного уравнения второго порядка в ограниченной области с локальными краевыми условиями. На линии изменения типа уравнения применены разрывные условия сопряжения для следа функции и следа производной. В качестве основного метода доказательства разрешимости поставленной задачи был использован метод конечных интегральных преобразований. При этом вопрос разрешимости задачи был эквивалентно редуцирован к вопросу разрешимости обыкновенных дифференциальных уравнений в соответствующих частях смешанной области. В частности, в области параболичности исходного уравнения было получено обыкновенное дифференциальное уравнение первого порядка, решение которого представлено в виде комбинации общего решения однородного уравнения и частного решения неоднородного. Определив коэффициенты в полученных общих интегралах дифференциальных уравнений, решение исследуемой задачи можно найти после применения обратного интегрального преобразования.

Статья в формате PDF

760 KB

уравнение в частных производных

краевая задача

разрывные условия сопряжения

интегральное преобразование Фурье

1. Елеев В.А., Гучаева З.Х. Об одной краевой задаче для уравнения гиперболо-параболического типа второго порядка в прямоугольной области // Известия Кабардино-Балкарского научного центра РАН. – 2011. – № 6. – С. 34–40.

2. Елеев В.А., Жемухова З.Х. О некоторых краевых задачах для одного смешанного уравнения с разрывными коэффициентами в прямоугольной области // Владикавказский математический журнал. – 2002. – Т. 4. – № 4. – С. 8–18.

3. Лесев В.Н. Исследование разрешимости краевых задач для уравнения четвертого порядка методом конечных интегральных преобразований // Современные проблемы математики: материалы международной конференции. – Махачкала: ДГТУ, 2006. – С. 44–46.

4. Лесев В.Н., Желдашева А.О. Неклассическая краевая задача для смешанного уравнения второго порядка с интегральными условиями сопряжения // Известия смоленского государственного университета. – 2013. – № 3 (23). – С. 379–386.

5. Лесев В.Н., Желдашева А.О. Нелокальная краевая задача для уравнения смешанного типа второго порядка в характеристической области // Вестник Адыгейского государственного университета. Серия 4: Естественно-математические и технические науки. – 2012. – № 3 (106). – С. 52–56.

6. Лесев В.Н., Желдашева А.О. Об одной краевой задаче для смешанного уравнения с разрывными условиями сопряжения // Известия смоленского государственного университета. – 2012. – № 3 (19). – С. 392–399.

7. Лесев В.Н., Шарданова М.А. О разрешимости краевых задач для неоднородного уравнения высокого порядка с переменными коэффициентами // Theoretical & Applied Science. – 2014. – № 12 (20). – С. 101–103.

8. Лесев В.Н., Шарданова М.А. Применение метода конечных интегральных преобразований к исследованию краевой задачи для уравнения высокого порядка // Theoretical & Applied Science. – 2014. – № 5 (13). – С. 1–4.

9. Фарлоу С. Уравнения с частными производными для научных работников и инженеров: пер. с англ. – М.: Мир, 1985.

10. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. – М.: Наука, 1969.

Исследование разрешимости краевых задач для уравнений в частных производных является одним из основных разделов обширной теории дифференциальных уравнений. Особое место в подобных исследованиях занимают задачи для смешанных и смешанно-составных уравнений. Это обусловлено непосредственными связями уравнений смешанного типа с теорией интегральных уравнений, теорией интегральных преобразований и специальных функций, а также их прикладной значимостью в математической физике и биологии.

В настоящей работе в ограниченной односвязной области исследована классическая краевая задача для линейного неоднородного смешанного уравнения с переменными коэффициентами. Помимо классических краевых условий в постановке использованы разрывные условия сопряжения на линии изменения типа уравнения и условия согласования. Доказательство разрешимости задачи проведено методом конечных интегральных преобразований.

Постановка задачи

В области Ω = {z: 0 < x < ℓ, –t₂ < t < t₁} евклидовой плоскости точек z = (x, t) рассмотрим уравнение

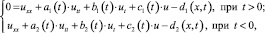(1)

где ℓ, t₁, t₂ – const > 0, a_i, b_i, c_i, d_i – достаточно гладкие функции (i = 1, 2).

Введем обозначения:

J = {z: 0 < x < ℓ, t = 0},

Ω₁ = Ω ∩ (t > 0); Ω₂ = Ω ∩ (t < 0);

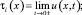
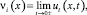
причем i = 1 если t → 0+; i = 2 если t → 0–.

Для уравнения (1) в области Ω исследована следующая

Задача A. Найти регулярное в Ω₁ ∪ Ω₂ решение u(x, t) уравнения (1) из класса

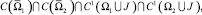
удовлетворяющее краевым условиям

u(0, t) = φ₁(t); u(ℓ, t) = ψ₁(t), t ≥ 0; (2)

u(0, t) = φ₂(t); u(ℓ, t) = ψ₂(t), t ≤ 0; (3)

u(x, t₁) = f₁(x); u(x, –t₂) = f₂(x), 0 ≤ x ≤ ℓ; (4)

условиям сопряжения

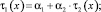
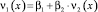(5)

и условиям согласования

f₁(0) = φ₁(t₁); f₁(ℓ) = ψ₁(t₁);

φ₁(0) = α₁ + α₂∙φ₂(0); ψ₁(0) = α₁ + α₂∙ψ₂(0);

f₂(0) = φ₂(–t₂); f₂(ℓ) = ψ₂(–t₂),

где φ_i, ψ_i, f_i – заданные функции из C¹, а α_i, β_i – заданные постоянные, такие, что α₂∙β₂ ≠ 0.

Доказательство разрешимости задачи А проведем методом конечных интегральных преобразований, по аналогии с работами [3, 8, 7].

Заметим, что краевые задачи в характеристических и прямоугольных областях для уравнений, представляющих частный случай уравнения (1), исследовались в работах [1, 2, 4, 5, 6].

Для сформулированной задачи необходимо рассмотреть следующие случаи:

1) a_i(t) ≠ 0;

2) a_i(t) = 0;

3) a₁(t)a₂(t) = 0, но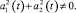

Легко видеть, что в случаях (2) и (3) оба или одно из условий (4) являются переопределяющими задачу.

В настоящей работе рассмотрим более подробно последний случай.

Пусть, например, a₁(t) = 0, а a₂(t) ≠ 0. Тогда уравнение (1) в области Ω₁ является уравнением параболического типа и принимает вид:

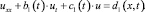
Далее проведем ряд преобразований пренебрегая первым из условий (4).

Применяя к последнему равенству конечное синус-преобразование Фурье [9]:

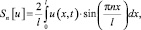
n = 1, 2, ... (6)

по переменной x на отрезке [0, ℓ] к уравнению (1) при t > 0, будем иметь

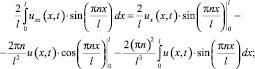
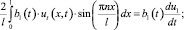
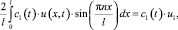
где u₁ = u_1n(t) – результат преобразования функции u(x, t) в Ω₁.

Подставляя полученные выражения в уравнение (6), приходим к параметрическому обыкновенному дифференциальному уравнению

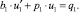(7)

Здесь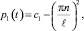

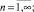
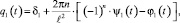– результат преобразования функции d₁(x, t).

Аналогично при t < 0 получим

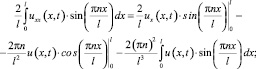
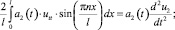
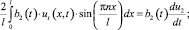
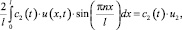
где u₂ = u₂(t) – результат преобразования функции u(x, t) в Ω₂,

Подставляя полученные соотношения в уравнение (1) при t < 0, приходим к следующему уравнению:

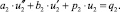(8)

Здесь

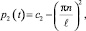
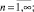
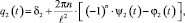
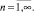
δ₂ = δ₂(t) – результат преобразования функции d₂(x, t).

Точно так же из (5) будем иметь

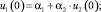
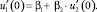(9)

Далее, проинтегрируем уравнения (7), (8). Если b₁(t) = 0, то u₁(t) сразу определяется из (7), в противном случае, как известно (например [10]), общее решение уравнения (7) имеет вид

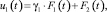(10)

где γ₁ – произвольная постоянная; F₁(t) – общее решение соответствующего однородного уравнения; F₂(t) – частное решение неоднородного уравнения.

Общее решение уравнения (7) может быть представлено в виде [2, с. 115]:

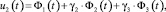(11)

где γ₂, γ₃ – произвольные постоянные; Φ₁(t) – частное решение неоднородного уравнения; Φ₂(t), Φ₃(t) – линейно независимые решения соответствующего однородного уравнения.

Из (10) и (11), с учетом (9), а также принимая во внимание (4), получим систему линейных алгебраических уравнений относительно постоянных γ₁, γ₂, γ₃:

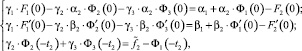(12)

где 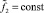– результат преобразования функции f₂(x).

Таким образом, вопрос однозначной разрешимости задачи (1)–(5) редуцирован к вопросу разрешимости системы (12). Применяя обратное преобразование [9]:

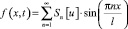
к функциям u₁, u₂, получим решение задачи (1)–(5) в областях Ω₁, Ω₂ в виде соответствующих рядов Фурье.

В заключение отметим, что случаи (1) и (2) исследуются аналогично.

Рецензенты:

Журтов А.Х., д.ф.-м.н., профессор, заведующий кафедрой геометрии и высшей алгебры, Кабардино-Балкарский государственный университет им. Х.М. Бербекова, г. Нальчик;

Хаширова Т.Ю., д.т.н., профессор, заведующая кафедрой системного анализа и компьютерных технологий управления, Кабардино-Балкарский государственный университет им. Х.М. Бербекова, г. Нальчик.

Библиографическая ссылка