Типичной задачей при моделировании гидродинамических процессов является расчет перепада или градиента давления при фильтрации текучих сред (ТС) через пористую среду в контрольном объеме, представленном ячейкой – элементом модели с плоскими гранями [5]. Модель элемента пласта – ячейки, представлена в виде параллелепипеда (или более сложной формы, но плоскими гранями), ограничивающего форму и размеры определенной части пласта (рис. 1).
Для удобства дальнейшего описания и вследствие явного подобия закона Дарси закону Ома в случае соблюдения линейного закона фильтрации будем понимать под гидравлическим сопротивлением ячейки i пласта между определенной парой граней отношение
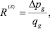 [Па?с/м3], (1)
[Па?с/м3], (1)
где S – ось, вдоль которой рассматривается течение в элементе; ?ps = pc – pgran – перепад давления между центром ячейки и одной из граней; qg – объемный расход флюида через грань g.
Таким образом, замыкающее отношение, соответствующее линейному закону течения Дарси вдоль оси S в ячейке, будет
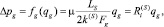 (2)
(2)
где S – ось – направление от центра ячейки к ее грани gran, 0 = X, 1 = Y, 2 = Z; Ls – длина ячейки вдоль оси S, м; Fgran – площадь грани (средняя площадь фильтрации), м2;
Сопротивление согласно (1) и (2):
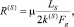 (3)
(3)
где k(s) – абсолютная проницаемость породы ячейки вдоль оси S, м2.
Направления фильтрации ТС будем условно полагать только вдоль осей X, Y и Z.
Наличие множества компонентов текучих сред при фильтрации учитывается согласно относительным проницаемостям. В этом случае сопротивление фильтрации компонента Ф вдоль оси S ячейки будет (рис. 1):
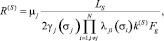 (4)
(4)
где ?j(?j) – функция относительной фазовой проницаемости (ОФП) компонента j от его объемной насыщенности – ?j, д.е.; ?j – динамическая вязкость компонента j, Па?с; ?ji(?i) – функция относительного изменения ОФП компонента j от насыщенности компонента i, д.е.; N – количество рассматриваемых компонентов, шт.
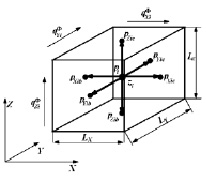
Рис. 1. Схема элемента гидродинамической модели (ГДМ)
Функция fg(qg) отражает закон фильтрации, иначе говоря, закон вязкостного внутрипорового трения, который также может быть получен через функцию градиента давления от скорости фильтрации:
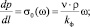 (5)
(5)
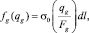 (6)
(6)
где ? = qg/Fg – скорость фильтрации через грань gran, м/с; qg – объемный расход среды, м3/с; ? – кинематическая вязкость, м2/с; kф – фазовая проницаемость, м2; ? – плотность флюида, кг/м3; ?0(?) – функция линейного закона внутрипорового трения; ? – объемная насыщенность, д.е.; m – текущая (так как она изменчива при изменении внутрипорового давления) пористость, д.е.
Описанные отношения (1)–(6) соответствуют линейному закону фильтрации.
Вследствие того, что при моделировании [1] реологических проявлений фильтрации в трещинах и высокопроницаемых каналах возникают существенные или сверхнизкие скорости течения флюидов с доминированием капиллярных сил, необходимо учитывать нарушение линейного закона.
Так как на данный момент вопрос нарушения закона фильтрации Дарси не исчерпан, здесь предлагается несколько вариантов математического описания моделей – законов фильтрации для учета результатов лабораторных исследований керна при их интегрировании в общую ГДМ месторождения.
1. Общий случай – нелинейные произвольные законы фильтрации. Нелинейный закон фильтрации (I приоритет) по функции корректировки градиента давления от числа Рейнольдса – ?I(?):
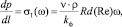 (7)
(7)
где Rd(Re) – функция, зависящая от числа Рейнольдса для пористых сред и показывающая увеличение или уменьшение сопротивления при изменении Re. Функция Rd(Re) равна 1 д.е., если линейный закон фильтрации соблюдается.
Данная функция может задаваться в исходных – настроечных данных формулой или табулирована с последующей интерполяцией.
Здесь 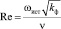 – число Рейнольдса, д.е., а
– число Рейнольдса, д.е., а 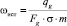 – истинная скорость фильтрации, м/с.
– истинная скорость фильтрации, м/с.
2. Общий случай – нелинейные произвольные законы фильтрации. Нелинейный закон фильтрации (II приоритет) учитывается в функции корректировки градиента давления в зависимости от истинной скорости ?II(?). Данная функция задается в исходных данных формулой или табулирована с последующей интерполяцией:
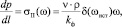 (8)
(8)
где ?(?ист) – зависящая от истинной скорости фильтрации и показывает увеличение или уменьшение сопротивления при изменении ?ист. Функция равна единице, если закон соответствует закону Дарси.
3. Частный случай – нелинейный составной закон фильтрации (III приоритет) – ?III(?).
Для расчета зависимости градиента давления от скорости фильтрации или наоборот требуется разделить закон фильтрации ?III(?) на две области определения:
– первая соответствует линейному закону фильтрации
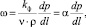
т.е. 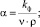 (9)
(9)
– вторая соответствует нелинейному закону фильтрации
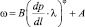
при 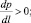 (10)
(10)
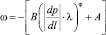
при 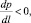 (11)
(11)
где ? – коэффициент, равный 1 Па/м; A и B – коэффициенты, отыскиваемые в процессе настройки ?III(?); ? – показатель нелинейности, д.е., который задается в исходных данных.
Переход от линейного к нелинейному закону фильтрации определяется числом Рейнольдса по Щелкачев:
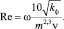 (12)
(12)
Критическая скорость и соответствующий ей критический градиент давления
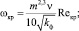
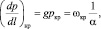 (13)
(13)
где Reкр – критическое число Рейнольдса (задается в исходных данных), д.е.
Коэффициенты A и B находятся решением системы уравнений:
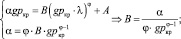 (14)
(14)
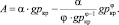 (15)
(15)
На рис. 2 показаны примеры составного закона фильтрации.
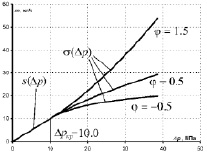
Рис. 2. Составной закон фильтрации для различных коэффициентов j при a = 1
Градиент давления при известной скорости фильтрации для данного (составного) закона фильтрации можно определить решением уравнения
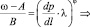 (16)
(16)
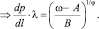 (17)
(17)
Основные отличия рассматриваемой здесь методики расчета fg(qg) заключаются в возможности гибкой настройки ГДМ для произвольных законов фильтрации, которые могут быть выявлены в результате проведения лабораторных испытаний пропускания ТС через керн в широком диапазоне расходов.
Фаза расчета перетоков между ячейками в ГДМ для любого момента времени в случае заданного закона фильтрации любым из предлагаемых способов требует решения нелинейного (в общем случае) уравнения относительно неизвестной скорости фильтрации при заданном перепаде давления между давлением в центре ячейки и среднего давления на каждой ее грани (рис. 3).
Неизвестный расход флюида – qg через грань – g можно рассчитать, решив уравнение вида
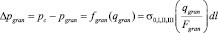 (18)
(18)
при известном перепаде давления ?pg.
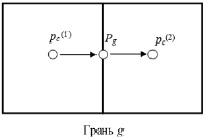
Рис. 3. Схема расчета перетока между ячейками
Учитывая возможность выбора четырех вариантов закона фильтрации из ?0(?), ?I(?), ?II(?) и ?III(?) в дальнейшем будем полагать закон вязкостного внутрипорового трения заданным для каждой ячейки в виде функций, связывающих градиент давления и скорости фильтрации ?i(?), где i – глобальный или локальный индекс ячейки. Если далее индекс не указан, то значит, имеется в виду общий случай.
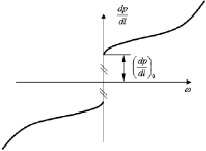
Рис. 4. Общий вид зависимости закона фильтрации
Как видно из графика (рис. 4), 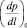 – критический градиент начала фильтрации, который складывается из градиента начала течения для флюида (задается в «PVT» свойствах флюида [2]) и из градиента начала фильтрации порового пространства пласта, который задается в свойствах каждого пласта.
– критический градиент начала фильтрации, который складывается из градиента начала течения для флюида (задается в «PVT» свойствах флюида [2]) и из градиента начала фильтрации порового пространства пласта, который задается в свойствах каждого пласта.
Решение уравнения для нахождения скорости фильтрации от градиента давления, создаваемого внешними силами при неучете второго закона Ньютона, происходит следующим образом: из сложившегося градиента давления вычитается критический градиент давления, а затем функция закона фильтрации принимается проходящей через начало координат. То есть решается уравнение относительно скорости фильтрации:
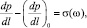 (19)
(19)
где ?(?) – закон фильтрации, который может быть одним из четырех приоритетов: линейный и нелинейные – I, II, и III.
Известно, что большинство фильтрационно-емкостных свойств (ФЕС) динамичны и изменяются в зависимости от внутрипорового давления.
Так, например, при изменении пористости, вызванном изменением внутрипорового давления, изменяется и абсолютная проницаемость, а следовательно, и все фазовые проницаемости (рис. 5). В общем виде ?m(?m) – это функция относительного приращения проницаемости от относительного приращения пористости.
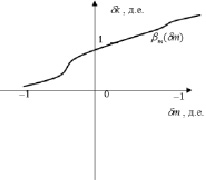
Рис. 5. Зависимость относительного изменения (множителя) проницаемости от относительного приращения пористости
Здесь величина 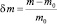 – относительное приращение пористости, д.е.; ?k – относительное изменение проницаемости при относительном приращении пористости, д.е.
– относительное приращение пористости, д.е.; ?k – относительное изменение проницаемости при относительном приращении пористости, д.е.
То есть итоговой абсолютной проницаемостью в любом из законов фильтрации будет
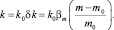 (20)
(20)
Также возможно предусмотреть корректировку абсолютной проницаемости от внутрипорового давления напрямую через функцию ?p(?p) (рис. 6).
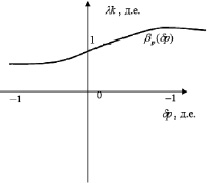
Рис. 6. Зависимость относительного изменения (множителя) проницаемости от относительного приращения давления
Здесь подобно предыдущему примеру 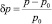 – относительное приращение давления, д.е.; p0 – начальное пластовое давление, которому соответствует начальная абсолютная проницаемость – k0; ?k – относительное изменение проницаемости при относительном приращении давления, д.е.
– относительное приращение давления, д.е.; p0 – начальное пластовое давление, которому соответствует начальная абсолютная проницаемость – k0; ?k – относительное изменение проницаемости при относительном приращении давления, д.е.
Данная функция необходима для учета изменения проницаемости от силы воздействия на пристеночную область – там, где ТС контактирует со стенками поровых каналов.
В этом случае итоговой абсолютной проницаемостью будет
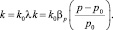 (21)
(21)
Полученная проницаемость в зависимости от выбранного закона фильтрации подставляется в соответствующее математическое описание (7)–(9).
Рассмотренное здесь математическое описание законов фильтрации интегрировано в ГДМ месторождений нефти и газа и используется в расчетном комплексе Hydra’Sym [2].
Результаты ряда лабораторных исследований авторов данной статьи и других ученых [3, 4] подтверждают необходимость учета в комплексной ГДМ месторождения нелинейных законов фильтрации, учитывающих уникальные особенности пористой среды в сочетании с физическими свойствами ТС.
В большей части случаев рассмотренного в статье математического описания достаточно для адаптации ГДМ посредством прямого переноса закона фильтрации из лабораторных исследований керна в модель через (7) и (8). Такие закономерности в целом сходны с видом функции на рис. 4 и отражают критический градиент давления начала течения, повышенные сопротивления на низких и высоких скоростях течения, линейный закон фильтрации на некоторых средних скоростях течения.
Рецензенты:
Грачев С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ «Тюменский государственный нефтегазовый университет», г. Тюмень;
Сохошко С.К., д.т.н., заведующий кафедрой «Моделирование и управление процессами нефтегазодобычи», Институт геологии и нефтегазодобычи, ФГБОУ «Тюменский государственный нефтегазовый университет», г. Тюмень.



