Основным признаком химических систем, позволяющим выделить их в отдельный класс из общей совокупности термодинамических систем, является измерение состава системы в результате протекания химических реакций. Для полной характеристики системы кроме задания любых двух переменных (давления и температуры, объема и температуры и др.) необходимо знать и состав системы – концентрации всех составляющих систему веществ. При этом целесообразно задавать такой минимальный набор веществ, который при известном механизме химических превращений позволял определять весь состав химической системы. Такой подход позволяет при изучении сложных явлений и проведении термодинамических расчетов использовать математические теории оптимального эксперимента [2–6].
В настоящей работе на основании результатов экспериментальных исследований процесса регенерации сульфатно-карбонатного расплава щелочных металлов путем восстановления монооксидом углерода (СО) построена адекватная математическая модель кинетики процесса, позволяющая оценивать изменения концентрации серы, оставшейся в расплаве, в зависимости от расхода СО.
В качестве исходных данных при построении искомой математической модели кинетики процесса восстановления сульфатно-карбонатных расплавов щелочных металлов СО использованы результаты экспериментальных исследований по установлению изменений концентрации серы в сульфатно-карбонатном расплаве в зависимости от расхода СО.
Эксперименты проводились с исходным содержанием сульфата натрия в расплаве – cin = 1,1 масс. % и cin = 2,1 масс. %, что в пересчете на мольное количество составляло cin = 0,68 ммоль/см3 и cin = 1,36 ммоль/см3 при температуре 550 °C и исходным содержанием сульфата cin = 1,36 ммоль/см3 при температуре 480 °C.
Расход подаваемого в расплав восстановителя – СО, во всех опытах был постоянным и поддерживался на уровне 1,5 см3/с.
Методика исследований и порядок проведения экспериментов подробно описаны в работе [1].
Математическая модель кинетики процесса восстановления сульфатно-карбонатных расплавов щелочных металлов монооксидом углерода (СО)
Полученные в работе [1] результаты показывают, что при обработке сульфатно-карбонатного расплава СО основное удаление серы из расплава начинается при минимальных расходах СО и достигает максимальных значений, при расходах восстановителя 8, 15 и 25 л соответственно, в зависимости от исходного содержания серы в исходной смеси – Cin = 1,1 масс. % и Cin = 2,1 масс. % и различной температуры (рис. 1).
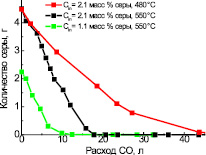
Рис. 1. Зависимость изменения содержания серы в сульфатно-карбонатном расплаве от расхода восстановителя – СО
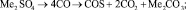 Me = Li, Na, K. (1)
Me = Li, Na, K. (1)
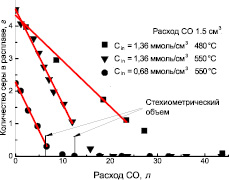
Рис. 2. Зависимость изменения содержания серы в сульфатно-карбонатном расплаве от расхода восстановителя – СО: прямые линии – результаты линейной аппроксимации экспериментальных кривых
Результаты линейной аппроксимации экспериментальных кривых показывают, что основное количество удаляемой из расплава серы, в зависимости от расхода СО, достаточно хорошо описывается прямыми линиями (рис. 2).
Нормализуя данные экспериментальных точек (рис. 2) для скорости реакции взаимодействия сульфатов щелочных металлов с монооксидом углерода, с учетом изменения расхода подаваемого СО (v), можно построить зависимость изменения концентрации сульфата в расплаве fs от величины v.
Значение величины v определяли исходя из выражения
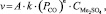
где А – площадь контакта расплава с газом СО; k – константа скорости реакции (1) (рис. 2); РСО – парциальное давление СО над расплавом; 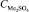 – концентрация сульфата щелочных металлов; n – порядок реакции.
– концентрация сульфата щелочных металлов; n – порядок реакции.
Расчетные значения fs определяли путем нормализации экспериментальных данных, исходя из выражения: fs = Cs/Cin, где Cs, Cin – концентрация серы в расплаве на данный момент времени и в исходном расплаве соответственно, моль/см3. Нормализуя значения СО для стехиометрического его объема, можно записать выражение, определяющее значения величины v = Vco/Vst, представляющего отношение объема СО, пропущенного через реактор Vco (Vco = t?r, где t – время, мин; r – скорость потока СО, см3/с) к стехиометрическому объему монооксида углерода Vst, который необходим по реакции (1). Значения величины Vst определяли исходя из выражения
Vst = 4Cin?Vмоль?Vmelt.
В результате нормализации экспериментальных данных и проведенных расчетов по определению значений fs и v для температуры 550 °C и различного содержания серы в исходном расплаве построены окончательные кривые, которые показаны на рис. 3.
Нетрудно видеть, что расчетные кривые аппроксимации достаточно хорошо описывают экспериментальные результаты.
Интересным представляется факт, что при температуре 550 °C расчетные кривые изменения концентрации серы в расплаве, несмотря на существенное (2 раза) различие концентрации серы в исходных расплавах – 0,68 и 1,36 ммоль/см3, на начальном участке удаления основного количества серы практически совпадают с экспериментальными кривыми. Это свидетельствует о том, что скорость реакции (1) определяется исключительно изменением концентрации сульфатов щелочных металлов в расплаве и для ее описания можно применять уравнение первого порядка.
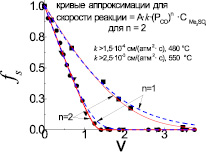
Рис. 3. Зависимость изменения концентрации серы fs от скорости протекания реакции (1), v
В термодинамической системе газ – расплав реакция взаимодействия газа с расплавом протекает на поверхности расплава. Тогда скорость протекания реакции (1) – v может быть определена исходя из выражения:
v = k?Ar?Cs?(PCO)n, (2)
где Ar – площадь контакта между расплавом и газом, см2; PCO – парциальное давление CO, атм.; k – константа реакции (1).
При выбранных параметрах константа скорости реакции k имеет размерность см/(атмn?с), где n – порядок реакции для давления CO, то есть n может быть теоретически любой целой величиной от 1 до 4. Так как значение свободной энергии Гиббса (?G) реакции (1) намного превышает величину произведения ?G >> RT (7 кДж/моль при 550 °C), обратной реакцией можно пренебречь. Тогда для описания кинетики реакции (1) можно применить следующие дифференциальные кинетические уравнения:
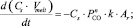 (3)
(3)
 (4)
(4)
где r – скорость потока CO внутри реактора, см3/с; PCO – парциальное давление CO, атм.; Р0 – стандартное парциальное давление, атм.; Vмоль – молярный объем газа, см3/моль.
Уравнение (3) описывает временную зависимость скорости изменения серы, оставшейся в расплаве, а уравнение (4) – зависимость скорости изменения количества CO над расплавом. Полученные уравнения также описывают поток СО в реакторе, количество СО, абсорбированное расплавом, и поток СО, выходящий из реактора.
Дифференциальные уравнения (3), (4) содержат два неизвестных параметра: константу скорости реакции k и порядок реакции – n.
Для расчета нормализованных кривых, приведенных на рис. 2, уравнения (3) и (4) были преобразованы в следующий вид:
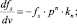 (5)
(5)
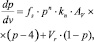 (6)
(6)
где fs = Cs/Cin – доля исходной концентрации серы, оставшейся в расплаве после процесса регенерации; Р = РСО/Р0 – парциальное давление CO над расплавом, (Р0 = 1 атм.); v = t?r/Vst – объем CO, пропущенный через реактор в относительных единицах, соответствующих стехиометрическому объему; Vst = 4Cin?Vмоль?Vmelt – объем СО исходя из стехиометрии реакции (1); kn = 4?k?Ar?Cin?Vмоль/r – нормализованная константа скорости реакции; Vr = Vst/Vfree; Ar = Vmelt?Cin?Vмоль/Vfree – безразмерные константы; Vfree – свободный от расплава объем, занимаемый газом, см3.
Решения уравнений (5), (6) относительно k и n, меняющихся при аппроксимации экспериментальных кривых при начальных условиях: fs = 1, Р = 0, v = 0, приведенных на рис. 2, позволили провести расчеты и построить кривые аппроксимации для fs = Cs/Cin и Р = PCO/P0 в зависимости от изменения величины v (рис. 4).
Расчеты проведены с использованием программы MathCad Software.
Сравнительный анализ полученных кривых с экспериментальными кривыми показывает, что оптимальное их соответствие наблюдается при n = 2 (сплошная линия на рис. 3). При n = 1 аналогичное соответствие получилось несколько хуже (пунктирная линия на рис. 3). При n = 3 для исследованных температур 480 и 550 °C соответствия расчетных кривых с экспериментальными данными практически не было обнаружено.
Расчетное значение порядка реакции (1) при n = 2 предполагает, что химизм протекания реакции описывается не одной стадией, а имеет более сложный механизм восстановления. На основании полученных данных нами рассчитаны константы скорости реакции восстановления сульфатно-карбонатных расплавов СО при температуре 480 °C и 550 °C, которые составили
k480 °C = 1,5?10–4 см/атм2?с
и k550 °C = 25,5?10–4 см/атм2?с.
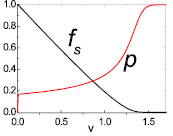
Рис. 4. Кривые аппроксимации для fs = Cs/Cin и Р = PCO/P0 в зависимости от v, полученные решением дифференциальных уравнений (5), (6) при n = 2 и T = 550 °C
Значения свободной энергии активации реакции (1), вычисленные с использованием полученных расчетных констант для температуры 480 и 550 °C, составили
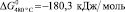
и 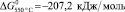
соответственно, что указывает на высокую термодинамическую активность протекания реакции (1).
Полученные данные позволяют провести оценку по выбору конструктивного размера реактора, необходимого для проведения процесса регенерации карбонатно-сульфатного расплава. Допустим, что тепловая электростанция мощностью 1 ГВт сжигает уголь с содержанием серы 5 % (масс.) и с коэффициентом полезного действия 45 %. Тогда в процессе деятельности данной ТЭЦ в атмосферу будет выбрасываться ~(0,05?1/0,45)?36 ≈ 3,9 кг/с серы (где 36 – среднее тепло от сгорания угля, MДж/кг).
В промышленных условиях процесс регенерации проводится в распылительных башнях, где концентрация сульфата и парциальное давление СО, получаемые в результате протекания реакции (1), могут сильно варьироваться. Принимая среднее парциальное давление СО равным 0,5 атм. и концентрацию серы в карбонатно-сульфатном расплаве (Cs) в пять раз меньше, чем в лабораторных опытах (0,136 ммоль/см3), можно определить требуемую поверхность контакта между расплавом и газом (Аind):
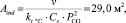 (7)
(7)
где П = 100 моль/с.
Если предположить, что в стандартной распылительной башне можно получать капли расплава диаметром 1 мм (Db = 1 мм), то общий объем капель с суммарной поверхности Аind = 29,0 м2 будет меньше, чем расчетное значение Аind?Db/6 ≈ 5 м3. Следовательно, минимальный объем расплава на стадии регенерации должен составлять несколько кубических метров. Это означает, что необходимый расход карбонатного расплава, требующегося для очистки газов ТЭЦ производительностью 1 ГВт, должен быть равен всего нескольким тоннам. При этом объемы необходимого количества карбонатного расплава не требуют строительства специальных реакторов и распылительных башен больших размеров, так как они легко могут вписываться в существующую инфраструктуру ТЭЦ [7].
На основании проведенных исследований и полученных результатов можно заключить, что использование данной технологии для глубокой очистки отходящих газов ТЭЦ позволит вовлечь в производство высококалорийные угли с большим содержанием серы и золы, без загрязнения окружающей среды выбросами SO2 и других вредных примесей.
Выводы
1. В настоящей работе на основании результатов экспериментальных исследований, полученных при восстановлении сульфатно-карбонатных расплавов щелочных металлов монооксидом углерода, построена математическая модель кинетики взаимодействия сульфатов щелочных металлов монооксидом углерода (СО).
2. Для описания кинетики реакции восстановления сульфатов щелочных металлов СО использованы дифференциальные кинетические уравнения, которые описывали: временную зависимость скорости изменения серы, оставшейся в расплаве; зависимость скорости изменения количества CO над расплавом; поток СО в реакторе; количество СО, абсорбированное расплавом, и поток СО, выходящий из реактора.
3. На основании решения дифференциальных уравнений определен порядок реакции и найдены значения константы скорости реакции для различных условий восстановления сульфатов монооксидом углерода. Построены кривые аппроксимации, описывающие изменения концентрации сульфата в расплаве и давления СО над расплавом в зависимости от изменения величины v – расхода подаваемого СО.
Библиографическая ссылка
Досмухамедов Н.К., Каплан В.А., Жолдасбай Е.Е., Досмухамедов Д.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КИНЕТИКИ ВОССТАНОВЛЕНИЯ СУЛЬФАТНО-КАРБОНАТНЫХ РАСПЛАВОВ ЩЕЛОЧНЫХ МЕТАЛЛОВ МОНООКСИДОМ УГЛЕРОДА // Фундаментальные исследования. – 2016. – № 2-1. – С. 38-42;URL: https://fundamental-research.ru/ru/article/view?id=39876 (дата обращения: 25.04.2024).



