При исследовании сложных систем часто приходится сталкиваться с необходимостью построения различных математических моделей. Классическими являются модели на основе решения систем дифференциальных уравнений, как обыкновенных, так и в частных производных. К более современным методам моделирования относятся формализм искусственных нейронных сетей (ИНС), нечеткая логика и другие методы искусственного интеллекта, теория вейвлетов и т.п.
Такие задачи имеют не только теоретическое, но и практическое значение. В частности, они могут быть существенной частью патентов.
В данной работе проанализированы различные подходы к моделированию динамики систем, в том числе основанные на методах искусственного интеллекта, а также их реализация в патентах.
Модели на основе систем дифференциальных уравнений
При исследовании сложных систем часто приходится сталкиваться с необходимостью построения математических моделей на основе систем дифференциальных уравнений, как обыкновенных, так и в частных производных. Такая задача имеет не только теоретическое, но и практическое значение. В частности, решение системы дифференциальных уравнений может быть существенной частью патентов определения динамических параметров системы.
Например, в [3] предлагается изобретение, которое относится к технике косвенных измерений координат летательного аппарата, которые могут быть использованы, в частности, в комплексных системах управления его полетом. Способ измерения координат основан на согласовании измерений дальностей летательного аппарата до группы наземных радиомаяков, находящихся в зоне его прямой видимости, с помощью позиционного навигационного датчика с оценками дальностей, получаемыми с помощью воспроизведения траектории летательного аппарата путем решения дифференциальных уравнений его движения, в которые подставляются измерения бортовых датчиков. Данный способ позволяет определять координаты летательного аппарата при произвольной траектории полета с высокой точностью, необходимой, например, при заходе на посадку, а также обеспечивает непрерывность определения координат при срыве измерений позиционного навигационного датчика, например, при маневрировании летательного аппарата.
Существенной частью практического применения дифференциальных уравнений и систем являются особенности применяемых численных методов их решения. Важность подобных задач привела к возникновению нескольких принципиально разных подходов к их постановке и решению. В частности, в [7] предлагается оригинальный подход, связанный с построением устойчивых алгоритмов решения систем дифференциальных уравнений, в основе которого лежит формализм искусственных нейронных сетей (ИНС). Данный метод, например, применим для параметризованных моделей, когда требуется исследовать поведение решения в зависимости от некоторого параметра, идентифицировать значение параметра по данным измерений или когда определяющие моделируемую систему характеристики заданы значениями, распределёнными в некоторых интервалах, – интервальными параметрами.
В качестве примера рассмотрим нейросетевую модель температурного поля по начально-краевым данным в случае коэффициента температуропроводности, заданного интервально. Математическая постановка задачи имеет вид
ut = ruxx, (x; t) ∈ (0; 1)×(0; T), r ∈ (r–; r+);
u(x, 0, r) = φ(x), x ∈ (0; 1); (1)
u(x, 0, r) = u(1, t, r) = 0, t ∈ [0; T].
Приближённое решение задачи можно искать в виде выхода нейронной сети:
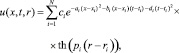
r ∈ (r–; r+). (2)
Обучение сети осуществляется через минимизацию функционала ошибки:
в котором первое слагаемое соответствует уравнению, второе – граничным условиям, третье – начальным условиям (одинаковым для образцов с разными значениями r); δb, δC > 0 – так называемые «штрафные» множители.
Здесь используются периодически перегенерируемые пробные точки:
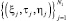
– в области Ω = (0; 1)×(0; T)×(r–; r+);
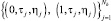
– на частях границы.
Особенностью метода является периодическая перегенерация пробных точек, что обеспечивает устойчивость решения.
Подобные модели имеют большую практическую ценность. Например, в [4] предлагается метод определения температурной зависимости коэффициента теплопроводности твердотельных изотропных электропроводящих материалов с использованием численного решения стационарного нелинейного дифференциального уравнения теплопроводности с внутренними источниками теплоты. Учитывается температурная зависимость коэффициентов теплопроводности и удельного электрического сопротивления. Способ применим для электропроводящих материалов, которые имеют выраженную зависимость коэффициентов теплопроводности и удельного электрического сопротивления от температуры в стационарных условиях для области высоких температур, например в области выше 2800 К для углеграфитовых материалов. Техническим результатом патента является повышение точности определения температурной зависимости коэффициента теплопроводности.
Методы искусственного интеллекта
В последнее время в исследовании динамики сложных систем стали применяться такие новые направления современной математики, как искусственные нейронные сети и формализм нечеткой логики. Приведем несколько примеров.
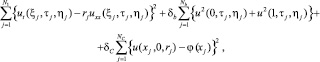
В [4] предлагается использовать рекуррентную ИНС для диагностики технического состояния электрических приводов, например электроприводов прокатных станов в металлургическом производстве. С определенным интервалом времени производятся замеры тока, напряжения, скорости и управляющего задания электропривода. Затем происходит преобразование параметров в цифровую форму и передача в персональный компьютер для обработки с помощью ИНС. Программно-реализованная и обученная на конкретном электроприводе перед его эксплуатацией рекуррентная ИНС воспроизводит динамику параметров электропривода, после чего производится сравнение результата динамики нейросетевой модели с реальной динамикой электропривода. В неисправном электроприводе возникает отклонение динамики его параметров от модели и рассчитывается функция рассогласования динамики. По характеру функции рассогласования динамики производится оценка технического состояния и прогноз ресурса электропривода. Техническим результатом применения изобретения является повышение точности и достоверности диагностирования аварийных состояний электропривода на работающем оборудовании в ранней и ненаблюдаемой стадии их возникновения, что предупреждает внезапную аварийную остановку электропривода и позволяет существенно снизить расходы на ремонт.
В [1] обработка результатов измерений с помощью ИНС сочетается с использованием методов нечеткой логики. Предлагаемое устройство относится к контрольно-измерительной технике и может быть использовано для непрерывного неразрушающего контроля, оценки и прогнозирования технического состояния конструкций корпуса судна в течение всего периода эксплуатации. На конструкциях корпуса судна регистрируют сигналы с блоков измерения, установленных в местах диагностирования конструкции, и сравнивают их с заранее зафиксированными значениями. При возникновении непредсказуемых (особенно нештатных и экстремальных) ситуаций с целью повышения надежности контроля реализуется технология обработки информации, использующая нейросетевые алгоритмы и методы принятия решений в нечеткой среде на основе бортовой ЦВМ в виде многопроцессорного вычислительного комплекса, нейрокомпьютера и процессора нечеткой логики.
Подобные разработки и исследования сложно выполнить без использования современных систем вычислительной математики. В частности, для исследования моделей на основе дифференциальных уравнений и систем хорошо подходит система Mathematica. Пример моделирования приведен в [2], где обсуждаются методы построения нейросетевой модели процессов тепломассообмена в грануле пористого катализатора. Приближённое решение задачи ищется в виде выхода искусственной нейронной сети (ИНС), параметры которой настраиваются на основе глобальной оптимизации. В работе рассматриваются гибридные методы, основанные на применении в процессе обучения нейронной сети результатов численных расчётов.
Данные работы потенциально имеют широкую область практического применения. В частности, в [6] предлагается изобретение, которое относится к катализаторам выхлопных газов и их использованию. Описан катализатор выхлопного газа, включающий в себя, по меньшей мере носитель и множество слоев, образованных на носителе, в котором, по меньшей мере один из множества слоев имеет внутри себя пустоты и содержит в качестве каталитических компонентов благородный металл, оксид алюминия и один или более смешанных оксидов, включающих в качестве главных компонентов оксид церия, оксид циркония и один или более редкоземельных элементов, исключая церий, где по меньшей мере один или более смешанных оксидов имеет удельную площадь поверхности не менее 40 м2/г при температуре 1000 °С. Описано устройство для обработки выхлопного газа, в котором на стороне выброса выхлопного газа из двигателя расположены один или более катализаторов выхлопного газа из указанных выше и в том случае, когда в нем имеется множество катализаторов выхлопного газа, каталитические компоненты катализаторов выхлопного газа являются одинаковыми или разными. Технический результат – предложенный катализатор выхлопного газа характеризуется повышенной эффективностью с одновременным усилением диффузии выхлопного газа в слой катализатора.
Что касается программных инструментов, для моделирования технических устройств наиболее подходящей является система Matlab с подсистемой визуального моделирования Simulink. Достоинством Matlab также является наличие подсистем нечеткой логики, ИНС, статистики и т.п., что позволяет использовать визуальное моделирование без написания кода программы, который генерируется автоматически. Также есть возможность получить автоматически сгенерированный С-код, после «заливки» которого в микроконтроллер можно получить устройство для управления реальным техническим объектом. В то же время данный программный продукт является достаточно дорогим, имеет ограниченное число вариантов лицензирования, а также имеет достаточно сложный собственный язык программирования.
Методы цифровой обработки сигналов
В области цифрового преобразования сигналов имеется достаточно много патентов на основе преобразования Фурье. Например, в [5] предлагается изобретение в области радиосвязи для поиска сигнала с использованием быстрого преобразования Фурье. Особенностью предлагаемого решения является то, что формирование взаимно корреляционной функции входного и опорного сигналов осуществляют на всей области неопределенности временных задержек входного сигнала, при этом делят указанную область неопределенности на перекрывающиеся интервалы длительности Т с областью перекрытия τ, вычисляют взаимно корреляционную функцию входного и опорного сигналов на каждом из указанных перекрывающихся интервалов. Значения взаимно корреляционных функций, вычисленные на указанных перекрывающихся интервалах и соответствующие одинаковым временным задержкам входного сигнала, суммируют. Устройство поиска сигнала с использованием быстрого преобразования Фурье содержит три запоминающих устройства, блок вычисления квадрата модуля, пороговый блок, блок быстрого преобразования Фурье, перемножитель, блок обратного преобразования Фурье, формирователь спектра опорного сигнала, блок синхронизации, блок задержки, блок коммутации и сумматор. Техническим результатом применения данного устройства является существенное уменьшение среднего времени поиска и снижение вычислительных затрат.
В то же время следует отметить практическое отсутствие патентов на основе вейвлет-преобразования.
Выводы
На основании обзора литературных источников и патентов можно сделать вывод, что в настоящее время происходит активное техническое воплощение современных математических идей и методов искусственного интеллекта, в частности в виде патентов. Очень перспективным в этом направлении представляется сочетание формализма искусственных нейронных сетей и формализма нечеткой логики.
В области цифровой обработки сигналов в патентах широко используется преобразование Фурье. В то же время следует отметить практическое отсутствие патентов на основе вейвлет-преобразования, хотя в будущем это направление представляется достаточно перспективным, и, как нам представляется, следует ожидать «всплеска» в этом направлении.
Библиографическая ссылка
Кондратьева С.Д., Семененко М.Г. МОДЕЛИРОВАНИЕ СЛОЖНЫХ СИСТЕМ: СОВРЕМЕННЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ И ПРАКТИЧЕСКИЕ АСПЕКТЫ // Фундаментальные исследования. – 2016. – № 5-1. – С. 43-46;URL: https://fundamental-research.ru/ru/article/view?id=40247 (дата обращения: 25.04.2024).



