Защита данных от несанкционированного доступа с целью ознакомления, искажения (подмены) или уничтожения – проблема, которую нельзя решить в принципе, но можно ослабить, придумывая все более изощренные методы шифрования. При этом криптостойкость шифра оценивается из экономических соображений: если раскрытие шифра «стоит» больше, чем сама зашифрованная информация, то шифр считается достаточно надежным.
В работах автора [1, 2, 3] приведены результаты исследований по повышению помехоустойчивости каналов связи путем применения алгоритма линейно-параметрической модуляции. При этом сигнал x(t) на выходе модулятора и в канале имеет вид последовательности фрагментов псевдослучайного сигнала, каждый из которых представляет собой результат свертки s(t) и сигнала-переносчика y(t) и может быть выражен в матричной форме
[x] = [y][s]
или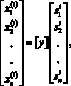 
i = 1, 2, ..., m. (1)
Матрица [y] квадратная n-го порядка, все строки ее получены из первой путем циклических перестановок.
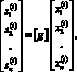
Для выделения полезного сигнала на приемной стороне принятый сигнал х(t) на фоне аддитивной помехи n(t) должен быть подвергнут линейному преобразованию вида
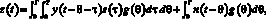(2)
где g(t) – импульсная характеристика демодулятора.
Модем, у которого импульсная характеристика демодулятора и несущее колебание выбраны из условия минимизации среднеквадратичного отклонения сигнала z(t) на выходе от модулирующего колебания s(t), назовем адаптированным к помехам в канале. У адаптированного модема характеристика демодулятора определяется выражением
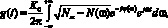(3)
где К0 – постоянное число; N(ω) – энергетический спектр помех в канале; Nm – постоянное число, превышающее пиковое значение N(ω); Ψ(ω) – произвольно выбранный фазовый спектр, а несущее колебание связано с импульсной характеристикой демодулятора матричным соотношением
[y] = [g]–1, (4)
где матрица [g] построена из отсчетных значений импульсной характеристики демодулятора на периоде Т путем циклических перестановок.
Отсчетные значения импульсной характеристики g(t) могут быть найдены по ее преобразованию Фурье
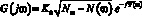(5)
с помощью следующих формул:
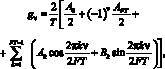(6)
ν = 1, 2, 3, ..., 2FT,
где А и В связаны с G(jω) соотношением
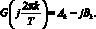(7)
Первая строка матрицы [y], полученной из соотношения (5), представляет собой отсчетные значения псевдослучайного сигнала на периоде Т.
Проходя через демодулятор с импульсной характеристикой g(t), сигнальная составляющая х(t) принятого колебания, учитывая (4), преобразуется в модулирующее колебание
i = 1, 2, ..., m. (8)
Приведенный алгоритм модуляции позволяет повысить помехоустойчивость и помехозащищенность при передаче сигналов. Покажем, что его можно применить и для шифрования сообщений, причем существенно повысить криптостойкость по сравнению с известными методами.
Один из методов шифрования основан на использовании псевдослучайных чисел [4]:
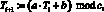(9)
где Тi – предыдущее псевдослучайное число, Тi+1 – следующее псевдослучайное число, а коэффициенты a, b, c постоянны и известны. Обычно последовательность псевдослучайных чисел имеет период с.
Шифруемое сообщение представляется в виде последовательности слов S0, S1, … , каждое длины N, которые складываются по модулю 2 со словами псевдослучайной последовательности Т0, Т1, … , то есть
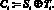(10)
Последовательность Т0, Т1, … называют гаммой шифра. Расшифрование сводится к сложению шифрованной последовательности с гаммой шифра:
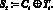(11)
Ключом шифра является начальное значение Т0, которое известно отправителю и получателю сообщения, то есть шифр относится к классу симметричных. Дешифровать сообщение можно только подбором ключа, при этом с увеличением N экспоненциально увеличивается криптостойкость шифра.
Метод считается простым и эффективным, однако если злоумышленнику известна хотя бы часть исходного сообщения, что на практике вполне возможно (многие текстовые редакторы помещают в начало файла документа одну и ту же служебную информацию), то все сообщение может быть легко дешифровано. Пусть известно одно исходное слово Si, тогда
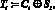(12)
и далее вся правая часть гаммы шифра определяется по указанной формуле датчика псевдослучайных чисел.
Один из путей повышения криптостойкости подобных шифров – применение вместо суммирования по модулю два более сложной (но обратимой) операции для вычисления шифровки [5].
Шифрованное сообщение получают, свертывая (convolution) слова исходного сообщения с гаммой шифра, которую
находят либо по алгоритму (9), либо другим способом
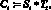(13)
где * – знак математической свертки.
Двоичное сообщение S, подлежащее шифрованию, разобьем на пакеты s1, s2, ..., si, ..., sL; здесь индексом обозначен номер пакета. Каждый пакет содержит N двоичных символов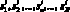 
. Гамма также может быть представлена последовательностью двоичных символов t1, t2, …, tn, …, tN. Тогда алгоритм шифрования можно записать следующим образом
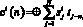(14)
Раскроем выражение (14) в виде системы уравнений
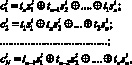
i = 1, 2, ..., L. (15)
Запишем систему уравнений в матричной форме
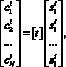i = 1, 2, ..., L. (16)
Матрица [t] квадратная N-го порядка, все строки ее образуются из первой путем циклических перестановок. Можно показать [14], что столбцы матрицы [t] линейно независимы, поэтому она невырождена (определитель не равен нулю), а значит, имеет обратную матрицу
[y] = [t]–1. (17)
Для расшифрования следует осуществить свертку принятого сообщения с обратной матрицей; назовем эту процедуру разверткой (deconvolution):
i = 1, 2, ..., L. (18)
Для проверки корректности алгоритма проведено компьютерное моделирование в программной среде Visual Studio 2012. На рис. 1–3 приведены диалоговые окна моделирования процесса шифрования – расшифрования.
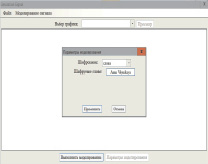
Сначала вводится текстовое сообщение, например, «Anna_Volynskaya», подлежащее шифрованию (рис. 1, а). Затем оно переводится в двоичную форму одним из известных кодов, например МТК-2 и представляется двоичным сигналом (рис. 1, б).
а б
Рис. 1.
а – ввод текстового сообщения, подлежащего шифрованию;
б – двоичный сигнал (код) передаваемого сообщения
а б
Рис. 2.
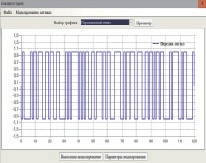
а – гамма шифра – двоичный псевдослучайный сигнал;
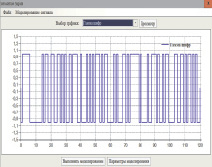
б – зашифрованное сообщение – шумоподобный сигнал
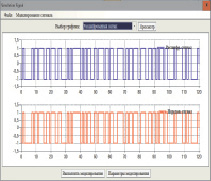
а б
Рис. 3.
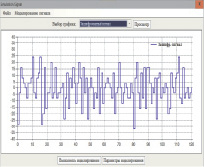
а – расшифрованный сигнал в сравнении с передаваемым;
б – расшифрованное сообщение
Гамма шифра, заранее полученная с помощью датчика случайных двоичных чисел и известная получателю сообщения, приведена в форме двоичного сигнала (рис. 2, а). Далее проводится операция свертки по алгоритму (14), в результате чего получается шумоподобный сигнал (рис. 2, б), который может быть передан непосредственно получателю в форме последовательности десятичных (или по другому основанию) чисел, соответствующих его значениям.
Для расшифрования сообщения получатель проводит свертку полученного сигнала с сигналом, полученным из гаммы шифра обращением матриц по формуле (17), в результате получает расшифрованный сигнал (рис. 3, а). Затем этот двоичный сигнал декодируется и получается исходное сообщение (рис. 3, б).
Результаты моделирования подтверждают корректность алгоритма. Способ может быть использован в системах с закрытым ключом для передачи сравнительно небольших, но важных сообщений. Длина фрагментов передаваемого сообщения ограничена временем и вычислительной устойчивостью процедуры нахождения обратной матрицы. В наших исследованиях применялись сообщения длиной до 500 двоичных разрядов.
Криптостойкость данного способа шифрования обусловлена необходимостью подбора обратной матрицы для расшифрования путем перебора. При этом каждый ее вариант требуется подвергнуть свертке с зашифрованным сигналом, что многократно замедляет процесс подбора и делает его практически бес-
полезным.
Библиографическая ссылка
СПОСОБ ЗАЩИТЫ ДАННЫХ ПРИ ПЕРЕДАЧЕ ОТВЕТСТВЕННОЙ ИНФОРМАЦИИ ПО ОТКРЫТЫМ КАНАЛАМ // Фундаментальные исследования. – 2016. – № 8-1. – С. 19-23;URL: https://fundamental-research.ru/ru/article/view?id=40528 (дата обращения: 24.04.2024).