Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Калмыков В.В. 1 Барков А.В. 1

---

1 Калужский филиал ФГБОУ ВО «Московский государственный технический университет им. Н.Э. Баумана (национальный исследовательский университет)»

Настоящая статья посвящена исследованию влияния режимов резания – глубины резания t и подачи на зуб Sz – на величину упругих отжатий концевой фрезы при контурном фрезеровании. Были получены математические модели упругих деформаций. Проведено сравнение адекватности теоретической и экспериментальной моделей. Экспериментальная математическая модель была получена по результатам экспериментов в виде уравнения регрессионного анализа. Полученная модель наглядно отражает степень влияния каждого из этих факторов на величину деформаций и может быть использована при подготовке производства для коррекции траектории режущего инструмента. Также проведен аналитический расчет упругих деформаций с использованием формул сопротивления материалов. Полученные результаты позволили сделать вывод об оптимальном количестве проходов для обеспечения требуемой точности.

Статья в формате PDF

0 KB

контурное фрезерование

концевая фреза

упругие деформации

технологическая система

1. Бысов С.А., Малышев Е.Н. Исследование технологических возможностей вертикально-фрезерного станка типа обрабатывающий центр // Инженерный вестник. – 2013. – № 11. – С. 3.

2. Калмыков В.В., Антонюк Ф.И., Зенкин Н.В. Выбор метода для автоматизации контроля состояния режущего инструмента // Южно-Сибирский научный вестник. – 2014. – № 3 (7). – С. 53–55.

3. Калмыков В.В., Космынина Е.В., Сорокин П.С. Выбор методов оценки точности технологических процессов // Инженерный вестник. – 2012. – № 8. – С. 4.

4. Калмыков В.В., Малышев А.Н., Покровская М.Э. Анализ способов точного позиционирования рабочих органов станков с ЧПУ // Инженерный вестник. – 2012. – № 7. – С. 1.

5. Малышев Е.Н., Мусохранов М.В., Калмыков В.В., Антонюк Ф.И. Распределение энергии технологического воздействия при формировании рабочих поверхностей деталей машин из металлических материалов // Современные проблемы науки и образования. – 2015. – № 1–1; URL: http://science-education.ru/ru/article/view?id=17560 (дата обращения: 08.06.2016).

6. Мусохранов М.В. Поверхностная энергия как показатель качества поверхностного слоя // Справочник. Инженерный журнал с приложением. – 2005. – № 12. – С. 62.

7. Справочник технолога-машиностроителя. В 2-х т. Т. 2 / под ред. А.Г. Косиловой и Р.К. Мещерякова. – 4-е изд., перераб. и доп. – М.: Машиностроение, 1986. – 496 с.

8. Суслов А.Г., Дальский А.М. Научные основы технологии машиностроения. – М.: Машиностроение, 2002. – 684 с.

9. Технология машиностроения: учеб. для вузов: в 2 т. / В.М. Бурцев и др.; под ред. Г.Н. Мельникова. – 3-е изд., испр. и перераб. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2012. – 551 с.

10. Фролов В.К., Гладский М.Н. Аналитическое решение задачи определения упругих деформаций инструмента при контурном фрезеровании концевыми фрезами // Вестник Национального технического университета Украины «Киевский политехнический институт». – 2011. – № 63. – С. 171–174.

Одной из основных задач любого технологического процесса обработки резанием является обеспечение точности деталей [1, 2].

Известно, что на конечную точность получаемых деталей влияет множество факторов [3]. Рассмотреть и проанализировать их все в процессе механической обработки невозможно и во многих случаях экономически нецелесообразно. По этой причине более приемлемым решением является определение таких факторов, которые вносят наибольший вклад в снижение точности деталей и их компенсирование [5, 6].

Упругие деформации технологической системы зависят от выбранной схемы обработки. Они возникают под действием силовых факторов, всегда появляющихся при функционировании технологической системы. В общем случае деформации можно рассчитать по следующей формуле [8, с. 117]:

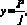
где P – силовой фактор; j – жесткость технологической системы.

В простейшем случае, если и силовые факторы, и жесткость системы являются постоянными величинами, упругие деформации могут быть рассчитаны и компенсированы предварительной настройкой технологической системы.

Однако на практике обе величины являются не постоянными, а изменяющимися, что вызывает колебание величины деформаций. Это делает невозможной их предварительную компенсацию.

Основными причинами, вызывающими изменение силовых факторов, являются: изменение глубины резания, вызванное колебаниями припусков; различная твердость разных участков обрабатываемой заготовки; износ режущего инструмента.

Жесткость технологической системы j зависит от жесткости её составных частей: жесткости приспособления, жесткости инструмента, жесткости оборудования, жесткости заготовки и т.д.

В настоящее время для компенсации деформаций технологической системы используются различные системы регулирования динамической настройки. Блок-схема одной из таких систем, разработанная в МГТУ Н.Э. Баумана, приведена на рис. 1 [9, с. 206].

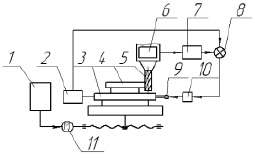
Рис. 1. Блок-схема адаптивной системы, обеспечивающей компенсацию упругих деформаций технологической системы

На фрезерном станке с ЧПУ обрабатывается заготовка 4 концевой фрезой 5. Управление приводами 11 подач осуществляет устройство ЧПУ 1. Возникающие при обработке силы резания вызывают упругие деформации технологической системы, фиксируемые датчиком 6. Заданное управляющей программой положение контролирует датчик 2. Сигналы датчиков сравниваются в сумматоре 8. При возникновении сигнала рассогласования последний усиливается усилителем 7 и подается на вход исполнительного элемента привода управления 9. Исполнительный элемент 9 сдвигает верхнюю плиту накладного динамометрического стола 3 вместе с установленной на ней заготовкой относительно стола 10 станка. Расстояние и направление корректирующего перемещения соответствуют значению и направлению деформации технологической системы [9, с. 206].

Данные системы имеют ряд преимуществ, например возможность оперативно подстроиться под изменяющиеся условия обработки. Недостатком представленных систем является недостаточная скорость срабатывания; их применение ограничивает их высокая стоимость. Поэтому в некоторых случаях избавиться от погрешностей обработки, вызванных упругими деформациями, рекомендуют другими способами, в частности прогнозированием распределения деформаций по длине обрабатываемого участка с внесением коррективы на этапе подготовки производства (например, соответствующим образом исказив траекторию движения режущего инструмента) [4, 9].

Расчет упругих деформаций

Расчет упругих деформаций включает в себя три этапа: расчет силовых факторов, действующих на фрезу; составление расчетной схемы и сам расчет упругих деформаций.

Расчет сил, действующих на фрезу в процессе работы, произведен по формулам теории резания. Известно, что при обработке на зуб фрезы действует окружная Pz, радиальная Py и осевая Px силы. Сила Pz может быть рассчитана по следующей зависимости [7, с. 282]:

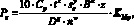
где t – глубина резания; Sz – подача на зуб; B – ширина фрезерования; z – число зубьев фрезы, D – диаметр фрезы; n – частота вращения шпинделя. Cp, y, n, q, w, KMp – поправочные коэффициенты, значения которых выбраны по рекомендациям [Там же, c. 282]. Радиальная составляющая силы резания Py может быть определена как часть от силы Pz по формуле [Там же, c. 292].

Py = 0,85?Pz.

При составлении расчетной схемы рассмотрена часть технологической системы: фреза, закрепленная в патроне, и заготовка. Это позволит не учитывать при расчете влияние жесткости других частей системы и упростит расчет. Установленную в патроне фрезу можно представить в виде консольно закрепленной балки, на свободный конец которой действует распределенная нагрузка:

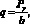
где Py – радиальная составляющая силы резания; b – ширина фрезерования. Расчетная схема приведена на рис. 2.

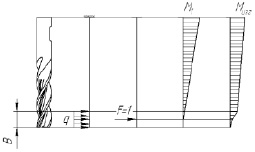
Рис. 2. Эпюры единичного и изгибающего моментов

Величину перемещения фрезы в любой точке её вылета удобно рассчитать по формуле, предложенной В.К. Фроловым и М.Н. Гладским [9, с. 173]:

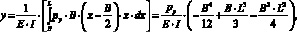
где L – вылет фрезы; E – модуль упругости материала фрезы; I(x) – момент инерции сечения фрезы в точке; B – ширина фрезерования. Для определения момента инерции фрезы в произвольном сечении были использованы данные работы [Там же, c. 172]. Результаты расчетов для каждого из вариантов приведены в табл. 1.

Таблица 1

Планирование эксперимента

В предлагаемой работе была поставлена задача получить математическую модель упругих деформаций технологической системы под действием сил резания, в зависимости от принятых режимов обработки, т.е. функцию вида y = f(t, Sz).

В качестве оборудования для исследования был использован фрезерный станок с ЧПУ модели MiniMill 450. Инструмент – концевая фреза HANITA 3615 диаметром 16 мм. Материал режущей части – быстрорежущая сталь. Обрабатываемый материал – Сталь 3. Ширина фрезерования B = 14 мм. Число оборотов шпинделя n = 525 об/мин. Вылет фрезы – 73 мм.

Для получения математической модели был проведен ряд экспериментов, в ходе которых изменялись значения глубины резания t и подачи на зуб Sz. Выбранная схема обработки приведена на рис. 3.

Объектом исследования является часть технологической системы, состоящая из концевой фрезы, установленной в шпинделе станка, и заготовки, установленной на столе.

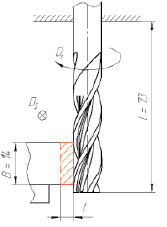
Рис. 3. Схема обработки

План эксперимента в виде расширенной матрицы представлен в табл. 2.

Таблица 2

В табл. 3 приведены значения факторов в натуральном и нормализованном масштабах.

Таблица 3

Расчет деформаций

Результаты эксперимента приведены в табл. 4.

Таблица 4

Зависимость деформаций от режимов резания имеет вид

y = 0,0375 + 0,0025?t + 0,075?Sz + 0,0025?t?Sz.

После вычисления коэффициентов регрессии и перехода от нормализованного масштаба к натуральному математическая модель примет вид

y = 0,325 – 0,01?t – 0,25?Sz + t?Sz.

На рис. 5 приведена схема проведения эксперимента и измерения упругих деформаций.

Для каждой из комбинаций параметров t и Sz было выполнено три прохода на длину li, равную 82, 52 и 22 мм. Во время работы под действием сил резания фреза отжималась от заготовки, из-за чего фактическая глубина резания tфакт была меньше расчетной t. Разность между этими глубинами резания является остаточной глубиной резания tост, равная упругой деформации фрезы. Величина tост измерялась как разность между соседними проходами при помощи измерительной головки с индикатором часового типа.

Анализ полученных результатов

В ходе выполнения работы упругие деформации технологической системы были определены тремя способами: экспериментально, рассчитаны по математической модели и с использованием формул теории резания.

Для удобства сравнения результаты объединены в табл. 5.

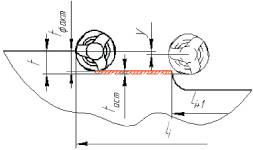
Рис. 5. Схема к расчету упругих деформаций

Таблица 5

Видно, что результаты всех трех способов отличаются. Наиболее близким к экспериментально полученным значениям оказался результат, рассчитанный по математической модели. Полученные значения оказались больше реальных, однако при обработке крупной партии деталей этот «запас» со временем может быть компенсирован за счет увеличения сил резания вследствие износа режущего инструмента.

Результаты расчета по формулам теории резания отличаются от реальных в меньшую сторону почти в два раза. Это вызвано тем, что при таком расчете не был учтен ряд факторов, влияющих на величину деформаций: изменение сил резания из-за колебания твердости обрабатываемой детали по длине и из-за износа фрезы, радиальное биение фрезы и т.д.

Выводы

Полученная математическая модель показывает, что влияние подачи на величину упругих отжатий фрезы значительно выше влияния глубины резания (почти в пять раз). Поэтому при контурном фрезеровании имеет смысл назначать как можно меньшую подачу на зуб и, чтобы сильно не снижать производительность, по возможности большую глубину резания.

В ходе проведения эксперимента было замечено, что разность остаточных глубин резания между вторым и третьим проходами пренебрежимо мала, то есть упругие деформации системы практически отсутствовали. Можно сделать вывод, что после второго прохода начался процесс «выхаживания» (практически без снятия материала с заготовки). Это значит, что при необходимости получения точной поверхности не имеет смысла увеличение числа проходов (свыше двух).

Библиографическая ссылка