Проблемы создания прикладных интеллектуальных систем поддержки принятия врачебных решений (ИСППВР) и экспертных систем широко обсуждаются в литературе, достаточно полный обзор которой приведен в [8]. Главным достоинством любой системы является качество ее базы знаний. Поэтому главный вопрос, решаемый при создании ИСППВР – это представление медицинских знаний.
Для решения интеллектуальной задачи в информационной системе необходимо решить следующие основные задачи:
- разработать формальную схему процесса решения задачи, представляющую из себя модель знаний о решении задачи;
- разработать формализмы представления этой модели (этих знаний) в ИСППРВР, т.е. модель представления знаний или логическую структуру базы знаний и формальные процедуры вывода решений;
- реализовать предложенную модель представления знаний и процедуры вывода решения.
Процесс решения задачи включает, как правило, два этапа: представление задачи и поиск решения. Успех решения задачи в значительной мере определяется формой ее представления. Формы и способы решения задачи зависят как от природы самой задачи, так и от человека, ее решающего.
Поиск удобной формы представления задачи является трудноформализуемым творческим процессом. Рассмотрим подход к представлению задачи выработки врачебного решения.
Представление задачи принятия врачебного решения
Описаны следующие наиболее употребительные способы представления задач:
- представление в пространстве состояний;
- представление путем сведения задачи к подзадачам;
- представление в виде теорем;
- комбинированное представление.
Представление задач в пространстве состояний заключается в описании всех состояний, или только начальных состояний и операторов, отображающих одни состояния в другие, и целевого состояния. Возможны различные формы описания состояний задачи (строки, векторы, матрицы, графы). Операторы могут быть заданы с помощью таблицы, связывающей каждое входное состояние с некоторым выходным.
Поиск решения в пространстве состояний заключается в нахождении последовательности операторов, отображающей начальное состояние в целевое. Решением задачи будет указанная последовательность операторов. Очевидно, что такое представление задачи задается тройкой (S, F, G), где S – множество начальных состояний, F – множество операторов, отображающих одно состояние в другое, G – множество целевых состояний.
Представление, сводящее задачу к подзадачам, заключается в разбиении исходной задачи на множество подзадач, раздельное решение которых дает решение исходной задачи. Каждая из подзадач, в свою очередь, может быть также разбита на подзадачи и так до тех пор, пока разбиение будет возможно. Очевидно, что разбиение заканчивается при достижении подзадач, решение которых известно. Такие задачи называются элементарными.
Представление в виде теорем используется для задач, которые можно представить в виде теорем, подлежащих доказательству. В этом случае задаются посылки (множество известных истинных утверждений – аксиом), затем формулируется теорема, доказательство которой позволяет получить решение поставленной задачи.
Комбинированное представление в общем случае используется для эффективного решения отдельных задач путем комбинирования различных способов представления задач.
Рассмотрим специфику принятия врачебного решения. Формально модель принятия врачебного решения можно представить в виде
M = <X, R, A>, (1)
где X – множество исходных данных для принятия решения, т.е. текущих показателей состояния здоровья; R – множество всевозможных решений, принимаемых на различных этапах обобщения информации; А – множество операций обработки информации и принятия решения.
Процесс обработки информации осуществляется поэтапно, и на каждом этапе реализуются лишь элементарные операции по переработке информации, то есть модель вида (1) всегда представима в виде последовательности:
М = <X, R1, a1> <R1, R2, a2> … <Ri–1, Ri, ai>, (2)
где X – множество исходных данных; R1, ..., Ri – множества промежуточных решений (обобщенных показателей объекта управления); a1, ..., ai – элементарные операции обработки (обобщения) информации; Ri – конечное решение;
R = {R1, ..., Ri};
A = {a1, ..., ai};
<Rn–1, Rn, an> – элементарная n-операция обобщения информации (n = 1, …, i); i – количество элементарных операций обобщения информации для выработки решения (глубина поиска решения в традиционном понимании).
Отметим, что каждое множество промежуточных решений можно рассматривать как множество исходных данных для очередного этапа обобщения информации, т.е., с содержательной точки зрения, R является состоянием пациента, на фиксированном уровне обобщения информации, а элементарные операции определяют правила перехода от нижнего к верхнему уровню обобщения информации о состоянии здоровья.
Выражение (2) можно представить в виде совокупности функций обработки информации, каждая из которых отображает соответствующее подмножество множества исходных данных X в одно решение множества R. Каждая такая функция представима в виде
Rm = fm(x1, ..., xN), (3)
где ym – элемент множества Y, m = 1, …, I; I – количество элементарных операций обработки информации; N – количество исходных данных; fm – функция, соответствующая элементарной операции обработки информации am.
В такой нотации процесс принятия решения можно представить в виде формулы
М = fi(fi–1(…f1(x1, …, xN)…)). (4)
Таким образом, модель процесса выработки врачебного решения (1) можно представить в виде графа функций обработки информации, где вершинами графа являются имена (описания функций), а дугами – направления переходов информации между функциями. Такую модель можно назвать аппликативной моделью предметной области (процесса выработки решения).
Построение аппликативно-фреймовой модели представления знаний
С содержательной точки зрения, аппликативную функцию обработки информации можно трактовать как одну из задач (подзадач), на которые можно декомпозировать исходную задачу (задачу выработки решения). В этой интерпретации можно считать, что задача выработки врачебного решения представима в виде разбиения исходной задачи на подзадачи. Задача описывается в виде графа, называемого графом редукции задачи. При этом вершинам будут соответствовать задачи, а дугам – операторы редукции задачи. Причем корню дерева соответствует исходная задача, вершинам 1-го уровня – задачи, непосредственно порожденные исходной задачей, вершинам 2-го уровня – задачи, порождаемые задачами 1-го уровня, и т.д. Кроме того, решение задачи соответствует значению функции обработки информации, а исходные данные задачи соответствуют параметрам функции обработки информации.
Если для решения вышестоящей задачи необходимо решение всех вытекающих из нее подзадач, то узлы графа, соответствующие этим подзадачам, называются связанными; в противном случае узлы называются несвязанными. Вершины графа, соответствующие задачам, которые могут быть решены, называются разрешимыми, не имеющим решения – неразрешимыми. Вершины, соответствующие элементарным задачам на самом нижнем уровне разбиения, называются заключительными. Следовательно, вершина, не являющаяся заключительной, будет разрешима, если разрешимы все ее дочерние связанные вершины или хотя бы одна из дочерних несвязанных вершин.
Поиск решения при сведении задачи к подзадачам опирается на граф редукции задачи, который является графом типа И-ИЛИ. Для описания формальных процедур поиска решения необходимо определить формализм неявного описания графа.
Традиционен подход к неявному представлению графа посредством описания операторов порождения подзадач [21]. Оператор преобразует исходное описание задачи в множество дочерних подзадач. Для конкретной задачи может существовать множество операторов преобразования. Применение каждого оператора порождает альтернативное множество подзадач, что определяет существование отношения ИЛИ на графе редукции.
В работе предлагается подход к представлению дерева подзадач в виде графа потока данных (ГПД).
Под ГПД [11, 21, 24, 28, 29, 31, 33, 34] понимается формализованное представление процесса обработки информации в целях решения задачи в виде графа, вершины которого есть функции обработки информации (правила обобщения), а дуги – потоки информации, проходящие через эти функции. Отметим основные черты, характеризующие ГПД:
1. ГПД наглядно и адекватно отображает процесс обработки информации при выводе решения.
2. ГПД отражает параллелизм и последовательность выполнения отдельных функций обработки информации.
3. Каждая функция инициируется, когда данные присутствуют на ее входе, и, следовательно, процесс обработки данных непрерывен, и ГПД отражает обработку данных в реальном масштабе времени.
Очевидно, что если вместо арифметических функций * и + использовать логико-лингвистические функции над понятиями предметной области, можно построить ГПД решения интеллектуальной задачи.
Рассмотрим формальный аппарат, который может быть предложен для описания ГПД, отражающего процесс принятия решения. Очевидно, в качестве такого аппарата должна выступать алгоритмическая теория, как например нормальные алгоритмы Маркова, машина Поста, машина Тьюринга, ?-исчисление или теория комбинаторов. В [6] доказана эквивалентность этих систем.
Представляется наиболее удачным использовать аппарат теории комбинаторов [1, 25, 26]. Поскольку теория комбинаторов является производной от теории ?-исчисления, следовательно, она обладает преимуществами, присущими ?-исчислению, а также специфическими уникальными свойствами. В [5] убедительно доказаны преимущества теории комбинаторов и описаны практические результаты. Покажем основные из них:
1. Теория комбинаторов является алгоритмической системой и позволяет формально описать все вычислимые функции.
2. Теория комбинаторов – бестиповая теория, все переменные, константы и функции трактуются как символы.
3. Все комбинаторы выразимы в минимальном базисном наборе комбинаторов.
В приведенной литературе дано подробное описание теории комбинаторов, но для дальнейшего изложения введем некоторые определения.
Пусть дан алфавит, состоящий из скобок (, ), символа <--> и букв латинского алфавита: A, B, ..., a, b, ... .
Тогда определим объекты по индукции:
если a – буква, то a – элементарный объект;
каждый элементарный объект есть объект;
если a и b – объекты, то (ab) – объект.
Примем соглашение, что объекты ab, a(bc) и abcd являются сокращениями для объектов (ab), (a(bc)), (((ab)c)d).
В данной нотации под комбинатором будем понимать объекты, с каждым из которых связана характеристическая функция изменения комбинаций переменных, к которым этот комбинатор применяется. Отметим, что комбинатор есть объект, в который не входит ни одной переменной. То есть, если комбинатор X последовательно применить к ряду объектов a, ..., ai, то возникающий новый объект Xa...ai конвертируется (преобразуется) в объект b, являющийся новой комбинацией объектов a, ..., ai. Это записывается в виде
Xa...ai → b.
Базисным набором комбинаторов называется совокупность комбинаторов, через которую выводимы все другие комбинаторы, но которые не выводимы друг из друга. Таким набором является следующий: {K, S}, где комбинаторы имеют следующие определения:
Kab → a (канцелятор);
Sabc → ac(bc) (коннектор).
Кроме того, полезными являются следующие комбинаторы:
Ia → a (тождество);
Babc → a(bc) (композитор);
Cabc → acb (пермутатор);
Wab → abb (дубликатор).
После введенных определений продемонстрируем представления ГПД в многомерных комбинаторах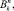 
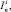Kn [21], имеющие следующие комбинаторные определения:
(C1)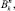
fg1 ... gkx1 ... xn = f(g1(x1, ..., xn)...gk(x1, ..., xn));
(C2)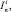 
x1...xi...xn = xi;
(C3) Kn xy1...yn = x.
В нотации этих комбинаторов каждую функцию обработки информации (3) можно записать в виде
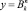fI1 ... Ik x1 ... xn, (5)
a всю модель (4) в виде
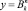fY1 ... Yk x1 ... xn, (6)
где f – функция отображения корневой вершины; Y1, ..., Yk – комбинаторные выражения нижестоящих узлов дерева; X1, ..., xn – исходные данные самого нижнего уровня; k – количество нижестоящих узлов; n – количество исходных данных.
Таким образом, дерево подзадач записывается в виде одной комбинаторной строки, представление которой в информационной системе не вызывает особых сложностей. Редукция комбинаторного выражения осуществляется согласно правилам C1-C3, что требует для вывода решения использования всего трех процедур вывода, а также процедур, реализующих функции отображения. Достоинством данного подхода является компактность хранимых определений и возможность проведения параллельной редукции. Интересные пути реализации машин потоков данных и других перспективных архитектур изложены в [5, 21, 31].
Покажем связь между многомерными комбинаторами и введенным ранее базисным набором комбинаторов {K, S} [25]:
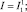
K = K1;
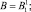
Kn = BKKn–1;
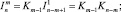
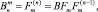
где
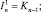
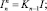
K0 = I; Fm = B(BSm–1)B;
Sm = B(BSm–1)S.
Для представления знаний о принятии врачебных решений в БЗ ИСППВР необходимо разработать такую модель представления знаний (МПЗ), которая позволяет формально описать граф редукции задачи (дерево подзадач), записанное в комбинаторной нотации. Причем необходимо предусмотреть два основных условия:
1. МПЗ должна поддерживать построение сетевых структур для представления графовых моделей знаний.
2. МПЗ знаний должна обеспечивать вывод значения при редукции каждой из вершин графа.
В литературе широко освещены такие основные МПЗ, как фреймовые, продукционные, логические, их модификации и семантические сети [15, 22]. Очевидно, требуемая модель должна совмещать свойства фреймовых моделей или семантических сетей для представления древовидных структур и продукционных или логических моделей для обеспечения вывода значений вершин дерева. В работе предлагается подход, объединяющий в себе свойства фреймовых и продукционных моделей, ориентированный на представление знаний о процессах принятия врачебных решений [10, 13, 17, 19, 23, 27, 30, 32].
Для представления конструкций вида (3) в виде, удобном для реализации в базе знаний, предлагается использовать формальную конструкцию – «аппликативный фрейм» (АФ), который можно задать в соответствии с традиционной нотацией в виде
N := (G, A1, ..., AM, F, E), (7)
где N – имя АФ; G – целевой атрибут АФ; A1, ..., AL – аргументы АФ; F – функция отображения АФ (отображающая значения аргументов фрейма в значении целевого атрибута), т.е. АФ обеспечивает аппликацию функции отображения к аргументам фрейма; E – функция объяснения вывода решения; L – количество аргументов АФ.
Связь между конструкциями (3) и (7) очевидна. Целевой атрибут АФ соответствует значению функции обработки информации, аргументы АФ соответствуют ее аргументам, а функция отображения АФ соответствует ее описанию.
Аппликативной модели предметной области соответствует дерево АФ, вершины которого являются именами АФ, а ветви – аргументами фреймов и (или) целевыми атрибутами. Целевой атрибут и аргументы определяются в области своих допустимых значений. Функция отображения задается списком операторов отображения, каждый из которых состоит из двух основных частей: списка условий и действия. Условие описывается в виде предикатов на подмножествах аргументов АФ, а действие описывается в виде различных выполнимых операций над аргументами, операций обращения к подпрограммам и к базам данных.
Описанную МПЗ необходимо расширить средствами ведения диалога, метасредствами управления редукцией и средствами объяснения решений и реализовать в комплексе инструментальных средств построения интеллектуальных систем поддержки приня-
тия решений.
Реализация модели
представления знаний
Вывод решения для аппликативно-фреймовой МПЗ должен осуществляться на двух уровнях:
1. Редукция всего дерева АФ.
2. Редукция одного АФ.
Редукция дерева АФ осуществляется путем последовательной редукции его вершин. Редукция осуществляется рекурсивной процедурой RED, заданной формальными правилами следующего вида:
(R1) RED[Ni] --> RED[(GNi, A1i, ..., AMi, Fi)].
(R2) RED[(Gi, A1i, ..., AMi, Fi) -->
--> EVAL[Fi, RED(A1i), ..., RED(AMi)].
(R3) RED[Ai] --> RED[Ni], Ai = GNi,
(R4) RED[Ai] --> #NR, Ai#(G1i, …, GNi),
где Ni – имя i-АФ; Gi – имя целевого атрибута i-АФ; Ami – имя m-аргумента i-АФ; Fi – имя функции отображения i-АФ; #NR – специальное значение терминальной вершины; i = 1, ..., I; mi = 1, ..., Mi; I – количество АФ, выделенных в предметной области; Mi – количество аргументов у i-АФ.
Правила (R1)–(R4) выполняют следующие действия:
(R1) – правило расширения; выполняется, если аргументом процедуры является имя АФ, и осуществляет поиск полной нотации АФ;
(R2) – правило редукции вершины дерева АФ, выполняется, если аргументом процедуры является конструкция полной нотации АФ, и осуществляет рекурсивное применение процедуры к аргументам АФ, с последующим применением функции EVAL, вычисляющей значение процедуры;
(R3) – правило перехода к следующему узлу дерева АФ; выполняется, если аргументом функции является имя аргумента АФ, при условии, что найден АФ, для которого этот аргумент является целевым атрибутом, и осуществляет рекурсивное применение процедуры к имени АФ, содержащему этот целевой атрибут;
(R4) – правило определения терминальной вершины, выполняется, если аргументом процедуры является имя аргумента АФ, причем этот аргумент не является целевым атрибутом никакого другого АФ, и присваивает процедуре специальное значение #NR (no references); в этом случае процесс редукции заканчивается.
Значением процедуры RED является либо значение процедуры EVAL, либо специальное значение #NR.
Алгоритм вычисления значения процедуры редукции EVAL формально задается следующими правилами:
(E1) EVAL [Fi,VG1i, ..., VGMi] --> APPLAY[Fi,VG1i, ..., VGMi].
(E2) EVAL[Fi, VGi1, ..., VGim-1, #NR, VGim+2, ..., VGiM] --> APPLAY[Fi, VGi1, ..., VGim-1, Am, VGim+2, ..., VGiM],
где VGi – значение целевого атрибута i-АФ, являющегося m-аргументом i-АФ; Am – имя m-аргумента i-АФ; #NR – специальное значение терминальной вершины.
Правило (E1) определяет состав аргументов и осуществляет инициализацию процедуры APPLAY, если среди аргументов процедуры не обнаружено терминальных символов #NR. Правило (E2) выполняется в противном случае и вместо терминального символа передает процедуре APPLAY значение соответствующего аргумента АФ.
Процедура APPLAY является традиционной процедурой интерпретаторов функциональных языков программирования и применяет функцию, являющуюся ее первым аргументом к последующим своим аргументам. Реализация функции APPLAY, которая и должна проводить непосредственное вычисление значения фрейма, представляет наибольшую сложность. Эта процедура фактически выполняет логический вывод целевого значения атрибута. Сложность этой процедуры определяется сложностью задания функции отображения.
Существует несколько способов задания механизма логического вывода, к которым можно отнести метод резолюций [19] и модифицированный метод резолюций для языка Пролог [2], обратный метод Маслова [12], метод секвенц-резолюций [9] и другие методы.
В экспертных системах большее распространение получили методы вывода решений на правилах [15]. В силу большей универсальности продукционных моделей функцию отображения наиболее удобно задать в виде совокупности правил продукций, где в левой части заданы условия на аргументах фрейма, а в правой элементарная функция вычисления целевого атрибута. В этой связи предложенная модель может быть классифицирована как фреймово-продукционная. Процедура APPLAY должна обеспечить выбор необходимого правила в соответствии с заложенным алгоритмом. Известны следующие основные алгоритмы [15]:
– выбор первого применимого правила;
– выбор по заранее заданному приоритету;
– выбор по вероятности;
– выбор наиболее применимого правила;
– выбор последнего примененного правила и т.д.
Редукция целевого АФ осуществляется формальной рекурсивной процедурой RED, заданной правилами R1–R4, значение которой есть значение целевого атрибута этого АФ. Начало редукции корневого АФ задается правилом R1.
Работа процедуры редукции заключается в определении значений аргументов АФ и применении его первого подходящего определяющего выражения из описания функции отображения этого АФ к значениям аргументов. Рекурсивность процедуры редукции позволяет говорить о редукции всего дерева АФ. Поэтому процесс вывода решения можно отождествить с процессом редукции дерева АФ.
В целях придания МПЗ свойств И-ИЛИ графа редукции в описание АФ необходимо ввести метаправила, которые инициализируются при начале редукции АФ. Каждое такое метаправило должно осуществлять альтернативный проход по дереву АФ. Этого можно достичь путем динамической модификации списка аргументов АФ: либо добавляя в него новые члены, либо исключая существующие.
Заключение
Предложенная МПЗ может лечь в основу построения системы знаний о выводе врачебного или управляющего решения. Реализация такой МПЗ может быть выполнена в различных системах программирования, хранение формализованных конструкций может быть осуществлено в различных системах управления базами данных.
Библиографическая ссылка
Лебедев Г.С., Лосев А.Ю. АППЛИКАТИВНО-ФРЕЙМОВАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ МЕДИЦИНСКИХ ЗНАНИЙ // Фундаментальные исследования. – 2016. – № 8-2. – С. 254-261;URL: https://fundamental-research.ru/ru/article/view?id=40651 (дата обращения: 19.04.2024).