Цель работы – усовершенствовать и добавить новые функции в существующий калькулятор передаточных функций в среде программирования Borland Delphi версии 5 [1]. Калькулятор создан на кафедре АТП БФ ПГТУ, предназначен для выполнения арифметических операций с передаточными функциями без запаздывания и используется для практических занятий по курсам «Теория управления» и «Автоматизация технологических процессов», а также в курсовом и дипломном проектировании студентами специальности «Автоматизация технологических процессов».
В отличие от обычного калькулятора, где математические операции производятся над константами в данном калькуляторе математические операции производятся над передаточными функциями.
Главная форма калькулятора представлена на рис. 1
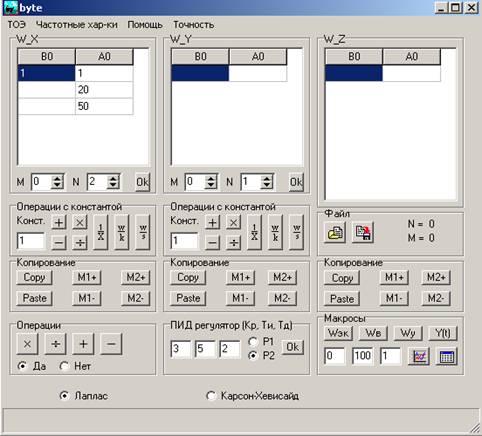
Рис. 1. Главная форма калькулятора
Калькулятор имеет две панели W_X и W_Y в которые вводятся передаточные функции операндов. Результат вычислений выводится на панели W_Z.
Передаточные функции представлены в общем виде:
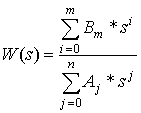
где m-порядок числителя, а n-порядок знаменателя;
![]() и
и ![]() – коэффициенты числителя и знаменателя соответственно.
– коэффициенты числителя и знаменателя соответственно.
Например для функции вида ![]() панель ввода будет выглядеть следующим образом (рис 2):
панель ввода будет выглядеть следующим образом (рис 2):
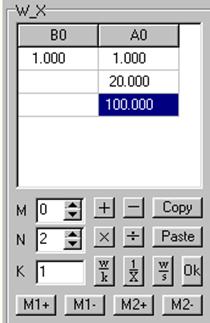
Рис. 2. Пример панели ввода.
В пределах одной передаточной функции в каждой панелей W_X и W_Y можно осуществлять математические операции с константой, введенной в окне К. Можно копировать передаточные функции через промежуточный буфер.
Для расширения промежуточного хранения результатов вычислений реализованы две дополнительные ячейки памяти М1 и М2, в которые можно копировать передаточные функции из любой панели или поместить передаточную функцию из выбранной ячейки в любую панель.
С помощью калькулятора над передаточными функциями можно производить операции вида: сложение, вычитание, умножение и деление.
Особенностью калькулятора является то, что с помощью него можно решать несколько видов электротехнических задач на нахождение тока и напряжения (рис. 3), на статических и динамических звеньях.
Также с помощью этого калькулятора можно вычислить аналитические выражения переходного процесса, корни характеристического уравнения и вывести график этой функции в графическом модуле (рис. 4)
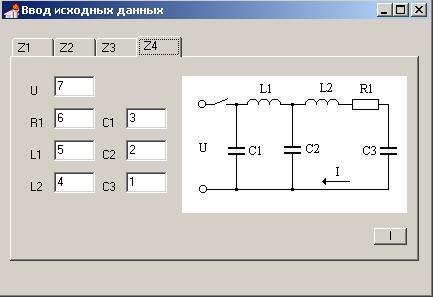
Рис. 3. Решение электротехнических задач.
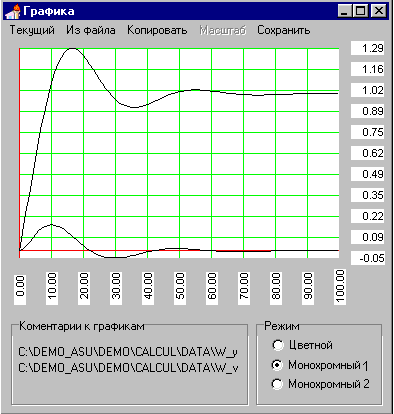
Рис. 4. Отображение переходного процесса.
В графическом модуле можно просматривать несколько графиков сразу, загружать их из файла и сохранять.
Опыт использования калькулятора в течение 5 лет выявил некоторые его недостатки. Для их исправления были поставлены следующие задачи:
- Исправить ошибки нахождения аналитической функции по передаточной
- Добавить возможности нахождения аналитической функции по передаточной с нулевыми и кратными корнями знаменателя
- Добавить возможности нахождения аналитической функции по передаточной с преобразованием Лапласа.
- Добавить алгоритм нахождения оптимальных настроек П, ПИ, ПД, ИД и ПИД регуляторов.
- Усовершенствовать калькулятор, так чтобы он мог производить операции с передаточными функциями с запаздыванием.
- Связать модули построения графика передаточной функции, нахождения оптимальной передаточной функции по этому графику и данного калькулятора.
- Связать калькулятор с базой данных, в которой будут храниться сами передаточные функции и их графики.
К данному времени выполнены первые три пункта из этого списка.
Для выполнения второго и третьего пункта было удалено старое и внедрено новое [2] преобразование Лапласа вида
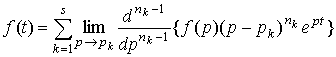 ,
,
где ![]() - полюсы
- полюсы ![]() , а
, а ![]() - их кратности.
- их кратности.
На практике очень часто требуется оптимизировать автоматическую систему регулирования, для этого требуется подобрать оптимальный регулятор и определить его оптимальные настройки. Выбор критерия оптимальности является одной из ответственных и сложных задач расчета системы регулирования. В практике наладки автоматизированных систем регулирования промышленных объектов химической технологии преобладает подход, связанный с минимизацией оценок качества регулирования вдоль границы области допустимых по условиям задачи заданного запаса устойчивости. Для выполнения четвертого пункта требуется найти запас устойчивости параметрической модели объекта регулирования. Для ее решения были найдены методы нахождения запаса устойчивости и оптимальных настроек регуляторов по методу расширенных комплексных частотных характеристик. В ближайшее время по этим методам будут составлены алгоритмы и в дальнейшем внедрены в виде одной из функций калькулятора.
После внесенных изменений, калькулятор передаточных функций позволяет находить оптимальные передаточные функции из эксперимента, далее проводить различные действия с передаточными функциями объектов регулирования, находить оптимальные воздействия, запасы устойчивости, в том числе для объектов с запаздыванием, характерных для предприятий химической технологии Верхнекамья.
Список литературы:
- Бильфельд Н.В., Беккер В.Ф. Имитационное моделирование систем цифрового управления.– Пермь: Пермский гос. техн. ун-т, 2002.– 52 с.
- Диткин В.А., Прудников А.П. Интегральное преобразование и операционное исчисление.– М.: Высшая школа, 1961.– 524 с.
Библиографическая ссылка
Кениг А.М., Бильфельд Н.В. КАЛЬКУЛЯТОР ПЕРЕДАТОЧНЫХ ФУНКЦИЙ // Фундаментальные исследования. – 2007. – № 12-2. – С. 221-224;URL: https://fundamental-research.ru/ru/article/view?id=4113 (дата обращения: 17.04.2024).



