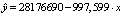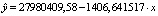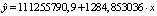Потребность в обеспечении высокоэффективной защиты производственного персонала, технологических процессов и продукции от загрязнений требует создания специфической защитной среды, называемой согласно ISO 14644-1, «чистыми помещениями», в которых контролируется счетная концентрация аэрозольных частиц. Их эксплуатация предполагает такое построение и использование, при котором сводится к минимуму поступление, генерация и накопление частиц внутри помещения, а также в котором при необходимости контролируются другие параметры, например температура, влажность и давление. В технике чистых помещений размерный диапазон контролируемых в воздухе частиц принято делить на три области: частицы диаметром от 0,1 мкм до 5,0 мкм; частицы диаметром менее 0,1 мкм (ультрамалые частицы); частицы диаметром более 5,0 мкм (макрочастицы). При определении счётной концентрации частиц в воздухе чистых помещений, измерения проводят, как правило, для частиц с диаметрами от 0,1 мкм до 5,0 мкм (наличие в воздухе частиц этого размерного диапазона положено в основу классификации чистых по классам чистоты) [4, 5, 7, 8].
Материалы и методы исследований
Распылитель с постоянным выходом (модель 3075/3076), генерирующий субмикронные аэрозоли. Средний размер получаемых капель составлял 0,3 мкм с геометрическим стандартным отклонением менее 1,9. Средний размер частиц аэрозоля уменьшался до 0,02 мкм путем распыления раствора диэтилгексилсебацината (DENS) в этиловом (или изопропиловом) спирте. Давление сжатого воздуха, подаваемого на распылитель, равнялось 2,0 кгс/см2. Для образования высокоскоростной струи сжатый воздух пропускался через входное отверстие диаметром 0,343 мм. В качестве рабочей жидкости для распыления использовали раствор диэтилгексилсебацината (DENS) в этиловом спирте. Для приготовления раствора DENS растворялся в спирте в пропорции 1:5. Рабочая жидкость подавалась в секцию распыления через вертикальные отверстия, а затем распылялась выходящей струей. Крупные капли, по принципу работы отделителя жидкости ударного типа, при ударе о противоположную стенку секции распылителя, стекали, за счет гравитационных сил, на дно секции распылителя, а тонко распыленная взвесь удалялась через верхний фитинг.
Использование разбавительных каскадов VKL, обусловлено потребностью в снижении концентрации аэрозоля без изменения размерного состава его частиц. В каскаде разбавления VKL гомогенно перемешивали определенное количество чистого воздуха с необходимым количеством аэрозоля в заданном константном соотношении. Посредством прохождения чистого воздуха извне, через систему эжекторных сопел, обеспечивалось создание пониженного давления, способствующего самовсасыванию аэрозоля. В используемом стенде задействованы два разбавительных каскада VKL с коэффициентом разбавления 100 в каждом каскаде и, соответственно, суммарный коэффициент разбавления равнялся 10000. Давление чистого воздуха, подаваемого на первый каскад, поддерживалось на уровне 2,0 кгс/см2, а подаваемого на второй каскад – 1,9 кгс/см2 в соответствии с кривыми калибровки каскадов. Воздух, без частиц, с объемным потоком чистого воздуха, обусловленным предварительным давлением, протекает через кольцевой зазор во всасывающее сопло. Из-за образуемого пониженного давления разбавляемый аэрозоль всасывается и гомогенно перемешивается с чистым воздухом в смесительной камере. При увеличении объемного потока чистого воздуха пропорционально увеличивается и скорость потока через кольцевой зазор. В результате этого пониженное давление у всасывающего сопла начинает расти, и объемный поток всасывания также увеличивается (оба объемных потока связаны с пониженным давлением и одинаково зависят от него).
Универсальный лазерный счетчик аэрозольных частиц Lighthouse Solair 1100+, предназначен для измерения концентрации аэрозольных частиц различного происхождения и химического состава с диаметрами от 0,1 до 5 мкм. Скорость прокачки анализируемого воздуха равна 28,3 л/мин. Принцип действия счетчиков аэрозольных частиц Lighthouse основан на регистрации рассеянного аэрозольной частицей света. В качестве источника света в счетчике используется гелий-неоновый лазер. Измерительная камера представляет собой эллиптическое зеркало. Частицы, попадая в освещенный рабочий объем оптической системы, создаваемый в одном из фокусов, рассеивают излучение, которое регистрируется фотоприемником, расположенном во втором фокусе. Прямое излучение поглощается световой ловушкой, выполненной в виде абсолютно черного тела. Интенсивность светового импульса пропорциональна размеру частицы, а количество световых импульсов определяет число аэрозольных частиц. Прокачка анализируемой пробы осуществляется встроенным насосом.
Массовый расходомер FM-380 рассчитан на точное и надежное измерение и/или регулирование массового расхода газов. Принцип работы основан на зависимости между скоростью потока и теплоотдачей проволочки, помещенной в поток и нагретой электрическим током. Расходомер FM-380 вместе с блоком FM-280 позволяет поддерживать стабильный расход воздуха.
Цифровой манометр «Диптрон 3» позволяет измерять дифференциальный перепад давления на образце фильтровального материала с точностью 0,25 %. Принцип работы: образуемый в датчике давления пропорциональный давлению сигнал постоянного тока подводится к подключенному последовательно усилителю результатов измерения и передается дальше в виде аналогового значения на преобразователь переменного/постоянного тока или же на шкальный прибор сети. Индикация осуществляется посредством светлых светодиодов на семи сегментах (диоды LED). Преобразователь переменного/постоянного тока сконструирован в технике CMOS.
Методика проведения испытаний
При проведении исследований был использован испытательный стенд (рисунок).
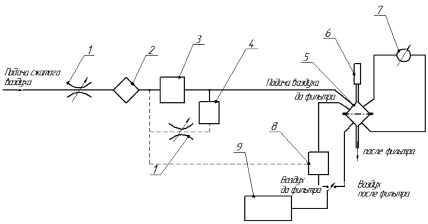
Испытательный стенд: (1 – регулятор расхода воздуха, 2 – фильтр, 3 – измеритель расхода воздуха, 4 – генератор аэрозоля, 5 – держатель, 6 – зажимный пневмоцилиндр, 7 – манометр, 8 – разбавитель аэрозоля, 9 – лазерный счетчик частиц)
Для проведения измерений образец фильтровального материала помещали в держатель (5) и фиксировали с помощью пневмоцилиндра (6). Посредством регулятора расхода воздуха (1) задавали требуемый расход воздуха. Сопротивление потоку воздуха определяли на основе показаний дифференциального манометра.
Для определения эффективности фильтрации включали генератор аэрозолей путем подачи на него воздуха давлением 2,0 кгс/см2. Воздух до фильтра подавали на лазерный счетчик через разбавительный каскад и определяли количество частиц разных размеров, попавших на образец. Воздух, после фильтра, снова подавали на лазерный счетчик, производили замер количества частиц, подаваемых на образец. Сжатый воздух (подаваемый на регулятор расхода воздуха, генератор аэрозолей и разбавительный каскад) очищался согласно соответствующему классу ИСО 5 по стандарту ГОСТ Р ИСО 14644-1. Кратность замеров – 15. Проскоки Р и эффективность Е определяли в % и вычисляли по следующим формулам:
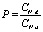 и E = 1 – P,
и E = 1 – P,
где CN.d – концентрация частиц после фильтра (численная); CN.u – концентрация частиц до фильтра (численная).
Обработку результатов проводили с использованием табличного процессора MS Excel, ведь к наиболее существенным достоинствам электронных таблиц следует отнести широкие возможности математического, статистического и графического анализа данных, эффективное моделирование проблем различного вида, прямой доступ к внешним базам данных, развитый интерфейс с другими популярными пакетами, поддержка средств мультимедиа, наличие инструментария для работы в сети Интернет. В настоящее время существуют сотни различных приложений, выполненных в виде надстроек к MS Excel и предназначенных для решения широкого круга задач – от математического и статистического анализа данных до реализации систем искусственного интеллекта [1–3, 6, 9, 10].
Результаты исследования и их обсуждение
Результаты замеров количества частиц, подаваемых на образец, представлены в табл. 1.
Таблица 1
Показатели замеров количества частиц, подаваемых на образец
|
№ образца |
Диаметр частиц, мкм |
Количество частиц |
|||||
|
до фильтра |
после фильтра |
||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
||
|
1 |
0,20 |
18490000 |
18850000 |
18910000 |
288 |
361 |
343 |
|
0,25 |
22330000 |
23130000 |
22300000 |
579 |
686 |
697 |
|
|
0,30 |
123560000 |
122760000 |
123630000 |
6447 |
6216 |
6155 |
|
|
2 |
0,20 |
19890000 |
18400000 |
19230000 |
452 |
553 |
601 |
|
0,25 |
23560000 |
22110000 |
23060000 |
772 |
796 |
724 |
|
|
0,30 |
128390000 |
124150000 |
130830000 |
16866 |
17399 |
18237 |
|
|
3 |
0,20 |
15760000 |
16390000 |
17470000 |
9276 |
9386 |
9766 |
|
0,25 |
20230000 |
21590000 |
22420000 |
4318 |
4843 |
4563 |
|
|
0,30 |
126640000 |
125100000 |
131360000 |
3990 |
4246 |
4156 |
|
|
4 |
0,20 |
49080000 |
47640000 |
46990000 |
2256 |
2262 |
2117 |
|
0,25 |
36490000 |
34970000 |
35380000 |
766 |
799 |
783 |
|
|
0,30 |
92730000 |
86650000 |
95900000 |
659 |
675 |
599 |
|
Статистическая обработка результатов экспериментальных данных заключалась в проведении корреляционно-регрессионного анализа и оценке полученных результатов моделирования зависимости количества частиц, пропускаемых через фильтр, от вида фильтровальной бумаги и размера частиц (взаимосвязь между факторным признаком количества частиц до фильтрации (признак Х) и результативным признаком количества частиц после фильтрации (признак Y) в зависимости от диаметра частиц и вида бумаги).
В процессе статистического исследования потребовалось решение следующих задач: построить однофакторную линейную регрессионную модель связи признаков Х и Y и оценить тесноту связи признаков Х и Y на основе линейного коэффициента корреляции r; определить адекватность и практическую пригодность построенной линейной регрессионной модели, оценив: значимость и доверительные интервалы коэффициентов а0, а1; индекс детерминации R2 и его значимость; точность регрессионной модели; дать интерпретацию: коэффициента регрессии а1; коэффициента эластичности КЭ; остаточных величин εi.
Для качественной оценки тесноты связи η, на основе показателя коэффициента корреляции, использовали шкалу Чэддока с соответствующими значениями связи: 0,1–0,3 – слабая; 0,3–0,5 – умеренная; 0,5–0,7 – заметная; 0,7–0,9 – тесная; 0,9–0,99 весьма тесная. Результаты регрессионного анализа представлены в табл. 2.
Таблица 2
Результаты корреляционного анализа по испытаниям частиц
|
Диаметр частиц, мкм |
0,20 |
0,25 |
0,30 |
|
Множественный R |
0,344908 |
0,483273928 |
0,518809096 |
|
R-квадрат |
0,118961 |
0,233553689 |
0,269162879 |
|
Нормированный R-квадрат |
0,051189 |
0,174596281 |
0,212944638 |
|
Стандартная ошибка |
12228285 |
5166049,453 |
13140673,08 |
|
Наблюдения |
15 |
15 |
15 |
Оценка результатов построения регрессионных моделей для разных диаметров частиц показывает, что наибольшая сила взаимосвязи между признаками наблюдается у самых крупных частиц с диаметром 0,30 мкм.
Для оценки степени варьирования между испытаниями частиц проведен дисперсионный анализ (табл. 3).
Таблица 3
Результаты дисперсионного анализа
|
Для диаметра частиц 0,20 мкм |
|||||
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
2,62E + 14 |
2,62E + 14 |
1,755312205 |
0,208028 |
|
Остаток |
13 |
1,94E + 15 |
1,49531E + 14 |
– |
– |
|
Итого |
14 |
2,21E + 15 |
– |
– |
– |
|
Для диаметра частиц 0,25 мкм |
|||||
|
Регрессия |
1 |
1,06E + 14 |
1,06E + 14 |
3,961397 |
0,068008 |
|
Остаток |
13 |
3,47E + 14 |
2,67E + 13 |
– |
– |
|
Итого |
14 |
4,53E + 14 |
– |
– |
– |
|
Для диаметра частиц 0,30 мкм |
|||||
|
Регрессия |
1 |
8,27E + 14 |
8,27E + 14 |
4,7878211 |
0,047523448 |
|
Остаток |
13 |
2,2448E + 15 |
1,73E + 14 |
– |
– |
|
Итого |
14 |
3,07155E + 15 |
– |
– |
– |
Таким образом, оценка дисперсий испытаний показала, что наиболее адекватны полученные результаты у крупных частиц диаметром 0,30 мкм. Однако и у частиц 0,20 мкм остатки дисперсий также не велики.
В табл. 4 представлены результаты параметров корреляционно-регрессионного анализа.
Построение регрессионной модели заключалось в нахождении аналитического выражения связи между факторным признаком X и результативным признаком Y.
На основе исходных данных (xi , yi) производили расчет параметров а0 и а1 уравнения однофакторной линейной регрессии:
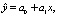
а также вычисление ряда показателей, необходимых для проверки адекватности построенного уравнения исходным (фактическим) данным. Рассчитанные коэффициенты а0 и а1 позволили построить линейную регрессионную модель связи изучаемых признаков в виде уравнений, определить коэффициенты корреляции и степени связи по шкале Чеддока (табл. 5).
Таблица 4
Результаты корреляционно-регрессионного анализа полученных значений
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P- Значение |
Нижние 95 % |
Верхние 95 % |
|
|
Для диаметра частиц 0,20 мкм |
||||||
|
Y-пересечение |
28176690 |
4579830 |
6,152344545 |
3,47463E-05 |
18282569 |
38070810 |
|
После фильтра |
– 997,599 |
752,9723 |
– 1,32488195 |
0,2080275 |
– 2624,3 |
629,0983 |
|
Для диаметра частиц 0,25 мкм |
||||||
|
Y-пересечение |
27980409,58 |
2086379 |
13,41099 |
5,45E-09 |
234730 |
3248775 |
|
После фильтра |
– 1406,641517 |
706,7393 |
– 1,9903 |
0,06800 |
– 2933,4 |
120,176 |
|
Для диаметра частиц 0,30 мкм |
||||||
|
Y-пересечение |
1125790,9 |
512256,97 |
21,7188 |
1,34E-11 |
10018917 |
122322402 |
|
После фильтра |
1284,853 |
587,1979 |
2,188 |
0,047523 |
16,2890910 |
2553,4169 |
Таблица 5
Линейная регрессионная модель связи изучаемых признаков
|
Диаметр частиц, мкм |
Модель |
Коэффициент корреляции, r |
Степень связи по шкале Чеддока |
|
0,20 |
|
0,344908 |
Слабая |
|
0,25 |
|
0,483273928 |
Умеренная |
|
0,30 |
|
0,518809096 |
Заметная |
Оценка практической пригодности синтезированной модели связи проводилась посредством анализа адекватности регрессионной модели (насколько построенная теоретическая модель взаимосвязи признаков отражает фактическую зависимость между признаками X и Y) в 4 этапа:
1) оценка статистической значимости коэффициентов уравнения а0, а1 и определение их доверительных интервалов для заданного уровня надежности;
2) определение практической пригодности построенной модели на основе оценок линейного коэффициента корреляции r и индекса детерминации R2;
3) проверка значимости уравнения регрессии в целом по F-критерию Фишера;
4) оценка погрешности регрессионной модели.
Следующим этапом была оценка статистической значимости коэффициентов уравнения а0, а1 и определение их доверительных интервалов. Так как коэффициенты уравнения а0, а1 рассчитывались, исходя из значений признаков только для 15-ти пар (xi, yi), то полученные значения коэффициентов являются лишь приближенными оценками фактических параметров связи а0, а1. Поэтому потребовалось: проверить значения коэффициентов на неслучайность (т.е. узнать, насколько они типичны для всей генеральной совокупности предприятий отрасли); определить (с заданной доверительной вероятностью 0,95) пределы, в которых могут находиться значения а0, а1 для генеральной совокупности наблюдений по образцам фильтровальной бумаги.
Затем, определяли значимость коэффициентов уравнения. Уровень значимости – это величина α = 1 – Р, где Р – заданный уровень надежности (доверительная вероятность). По умолчанию уровень надежности Р = 0,95. Для этого уровня надежности уровень значимости равен α= 1 – 0,95 = 0,05. Этот уровень значимости считается заданным.
Для каждого из коэффициентов а0 и а1 вычисляли уровень его значимости αр. Если рассчитанный для коэффициентов а0, а1 уровень значимости αр меньше заданного уровня значимости α = 0,05, то этот коэффициент признается неслучайным (т.е. типичным для генеральной совокупности), в противном случае – случайным. Сравнительная оценка полученных коэффициентов регрессии для разных диаметров пор бумаги 0,20, 0,25, 0,30 мкм показала, что наибольшая значимость этих коэффициентов наблюдается при диаметре пор бумаги 0,30, следовательно, именно данная модель регрессии является наиболее всего применимой и прогнозируемой именно для этого диаметра пор бумаги (табл. 6).
Таблица 6
Сравнительная оценка полученных коэффициентов регрессии
|
Диаметр частиц, мкм |
Уровень его значимости, αр |
Характеристика уровня значимости |
|
|
0,20 |
для а0 |
0,00000347463 |
Типичный |
|
для а1 |
0,208027502 |
Случайный |
|
|
0,25 |
для а0 |
0,000000000544933 |
Типичный |
|
для а1 |
0,068007528 |
Случайный |
|
|
0,30 |
для а0 |
0,0000000000000133891817883237 |
Типичный |
|
для а1 |
0,0475234476593554 |
Типичный |
|
Таким образом, только диаметр крупных частиц обеспечивает устойчивость полученной модели и надежность её оценки и прогнозирования.
В табл. 7 представлены границы доверительных интервалов коэффициентов уравнения от заданного уровня надежности для диаметров частиц 0,2; 0,25; 0,3 мкм.
Таблица 7
Границы доверительных интервалов коэффициентов уравнения
|
Диаметр частиц, мкм |
Коэффициенты |
Границы доверительных интервалов для уровня надежности Р = 0,95 |
|
|
нижняя |
верхняя |
||
|
0,20 |
а0 |
18282569,46 |
38070810,23 |
|
а1 |
– 2624,297167 |
629,0983391 |
|
|
0,25 |
а0 |
23473061,74 |
32487757,41 |
|
а1 |
– 2933,459006 |
120,1759727 |
|
|
0,30 |
а0 |
100189179,3 |
122322402,4 |
|
а1 |
16,28909104 |
2553,41698 |
|
Таким образом, построенные модели для разных видов фильтровальной бумаги показали, что наибольшее значение взаимосвязи между количеством отфильтрованных единиц и видом бумаги для диаметра частиц со значением 0,30 мкм. Дополнительно, пригодность построенной регрессионной модели для практического использования была оценена также и по величине индекса детерминации R2, показывающего, какая часть общей вариации признака Y объясняется в построенной модели вариацией фактора X.
Общая оценка адекватности регрессионной модели по F-критерию Фишера показала, что рассчитанный уровень значимости αр индекса детерминации R2, есть αр = 0,0475234476593556. Так как он меньше заданного уровня значимости α = 0,05, то значение R2 признается типичным, а модель связи между признаками Х и Y применимой для генеральной совокупности всех испытаний с диаметром частиц 0,30 мкм в целом. Погрешность регрессионной модели (в %) оценивали по величине стандартной ошибки, построенного линейного уравнения регрессии 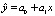 . Величину ошибки оценивали как среднее квадратическое отклонение по совокупности отклонений исходных (фактических) значений yi признака Y от его теоретических значений, рассчитанных по построенной модели. Учитывая, что в адекватных моделях погрешность не должна превышать 12–15 %, а это условие (10,9 %) выполнялось лишь для диаметра частиц 0,30 мкм, была подтверждена адекватность построенной модели
. Величину ошибки оценивали как среднее квадратическое отклонение по совокупности отклонений исходных (фактических) значений yi признака Y от его теоретических значений, рассчитанных по построенной модели. Учитывая, что в адекватных моделях погрешность не должна превышать 12–15 %, а это условие (10,9 %) выполнялось лишь для диаметра частиц 0,30 мкм, была подтверждена адекватность построенной модели 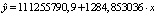 .
.
Заключение
В рамках проведения экспериментов по определению эффективности фильтрации разных образцов фильтровальной бумаги был проведен статистический анализ результатов экспериментальных данных, который позволил построить линейную регрессионную модель связи изучаемых признаков. Проведен анализ адекватности и практической пригодности построенной линейной модели, дана оценка статистической значимости коэффициентов уравнения а1 и а0, изучена зависимость доверительных интервалов коэффициентов а1 и а0 от заданного уровня надежности, определена практическая пригодность построенной регрессионной модели, дана оценка погрешности регрессионной модели, которая показала, что погрешность линейной регрессионной модели, соответствующая диаметру частиц 0,3 мкм, подтверждает адекватность построенной модели.
Расширение инструментов статистического анализа и дальнейшая обработка полученных результатов не имеет смысла ввиду того, что проведенный ранее анализ существующих технологических и конструктивных особенностей обеспечения высокоэффективной очистки подаваемого в чистые помещения воздуха, а также воздуха, образующегося в ходе технологических процессов и характеризующегося различным аэрозольным составом, определил дальнейшее направление экспериментальных исследований по оптимизации параметров, влияющих на эффективность очистки, связанное с геометрией конфигурации укладки фильтрующего материала [7].
Библиографическая ссылка
Маркелова Н.П., Демидова Л.Н., Черняев С.И. ОЦЕНКА РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ ФИЛЬТРОВАЛЬНОЙ БУМАГИ ДЛЯ ВЫСОКОЭФФЕКТИВНЫХ ФИЛЬТРОВ // Фундаментальные исследования. – 2017. – № 3. – С. 60-66;URL: https://fundamental-research.ru/ru/article/view?id=41395 (дата обращения: 25.04.2024).