Известно, что случайность параметров системы управления может оказывать существенное влияние на качество управления в статистическом смысле, например приводить к незапланированному изменению среднего значения выходного сигнала системы и росту его дисперсии. Указанные эффекты в целом характерны для стохастических систем, к которым может быть отнесено большинство реальных технических систем. Причиной данных эффектов является неизбежная статистическая связь между параметрами стохастической системы и ее выходным сигналом, что составляет главную проблему исследования этого класса систем [1].
Активная компенсация влияния случайности физических параметров на качество работы систем автоматического управления понимается в смысле формирования такого входного сигнала, который минимизирует влияние случайности параметров системы на ее выходной сигнал. Ранее авторами в статье [5] был предложен подход к решению задачи активной компенсации, основанный на пропорциональном изменении дисперсии случайной составляющей входного сигнала, компенсирующем влияние его детерминированной составляющей на дисперсию выходного сигнала стохастической системы. Данный подход был применен для компенсации случайности параметров электрогидравлического привода виброиспытательного стенда и показал возможность практически полного гашения нежелательных колебаний дисперсии формируемого вибрационного воздействия, обусловленных влиянием случайности параметров электрогидравлического привода при отработке случайного входного сигнала, содержащего гармоническую детерминированную составляющую.
В настоящей статье предлагается более общий подход к решению задачи активной компенсации в вышеуказанном смысле. В отличие от подхода, рассматриваемого в [5], где решалась задача компенсации периодических колебаний дисперсии выходного сигнала в установившемся режиме, в настоящей работе показана возможность эффективной компенсации искажения корреляционной функции выходного сигнала в переходном режиме. Кроме того, компенсация выполняется и для математического ожидания выходного сигнала.
Как и в работе [5], используется усредненная проекционная модель стохастической системы [4], построенная с применением методов теории матричных операторов [3]. Операторная форма этой модели позволяет сделать качественный вывод об аддитивном характере влияния случайности параметров системы на математическое ожидание и корреляционную функцию ее выходного сигнала и предложить соответствующие подходы к компенсации данного влияния.
Операторная форма математической модели стохастической системы
Общей формой математической модели рассматриваемого класса систем является стохастическое дифференциальное уравнение вида
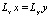 , (1)
, (1)
где y – гауссов случайный процесс (входной сигнал системы); Lx и Ly – линейные стохастические дифференциальные операторы:
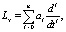
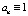 ,
, 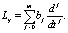
Предполагается, что все или некоторые коэффициенты ai, bj являются случайными величинами, определяемыми как
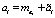 ,
, 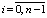 ,
,
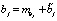 ,
, 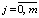 , (2)
, (2)
где 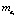 ,
, 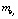 – математические ожидания;
– математические ожидания; 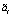 ,
, 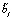 – центрированные гауссовы случайные величины. Начальные условия полагаются нулевыми. Система считается физически реализуемой, то есть выполняется условие n ≥ m.
– центрированные гауссовы случайные величины. Начальные условия полагаются нулевыми. Система считается физически реализуемой, то есть выполняется условие n ≥ m.
В монографии [1] показано, что для стохастического дифференциального уравнения Lx x = y , в предположении, что оператор Lx можно разложить на сумму двух операторов 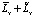 , где
, где 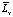 – обратимый детерминированный оператор, а
– обратимый детерминированный оператор, а 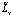 является случайной составляющей оператора Lx и имеет нулевое среднее (такое представление оператора Lx соответствует представлению коэффициентов ai в виде (2)), при определенных условиях возможно следующее представление решения:
является случайной составляющей оператора Lx и имеет нулевое среднее (такое представление оператора Lx соответствует представлению коэффициентов ai в виде (2)), при определенных условиях возможно следующее представление решения:
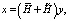 (3)
(3)
где 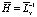 – детерминированный оператор;
– детерминированный оператор; 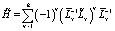 – стохастический оператор. В [1] дано строгое математическое обоснование справедливости представления (3).
– стохастический оператор. В [1] дано строгое математическое обоснование справедливости представления (3).
Заметим, что операторная форма (3) наглядно демонстрирует аддитивный характер влияния фактора случайности параметров стохастической системы (который не следует напрямую из представления 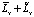 ). Усреднение выражения (3) позволяет найти статистические меры решения (математическое ожидание и корреляционную функцию выходного сигнала x).
). Усреднение выражения (3) позволяет найти статистические меры решения (математическое ожидание и корреляционную функцию выходного сигнала x).
Интегральные операторы 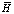 и
и 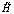 определяются в [1] через функцию Грина. При этом нахождение статистических мер решения (3) требует многократного интегрирования, что, к сожалению, не позволяет реализовать эффективный вычислительный алгоритм, опираясь только на результаты данной работы. С другой стороны, основываясь на результатах монографии [7], можно предложить внешне аналогичную операторную форму математической модели стохастической системы, которая, отличаясь другим математическим аппаратом, является более выгодной в вычислительном плане. Эта матрично-операторная форма, называемая проекционной моделью и являющаяся проекционным аналогом соотношения (3), получается в результате проекционной аппроксимации непрерывной модели (1) и имеет следующий вид:
определяются в [1] через функцию Грина. При этом нахождение статистических мер решения (3) требует многократного интегрирования, что, к сожалению, не позволяет реализовать эффективный вычислительный алгоритм, опираясь только на результаты данной работы. С другой стороны, основываясь на результатах монографии [7], можно предложить внешне аналогичную операторную форму математической модели стохастической системы, которая, отличаясь другим математическим аппаратом, является более выгодной в вычислительном плане. Эта матрично-операторная форма, называемая проекционной моделью и являющаяся проекционным аналогом соотношения (3), получается в результате проекционной аппроксимации непрерывной модели (1) и имеет следующий вид:
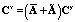 , (4)
, (4)
где 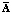 – детерминированный матричный оператор;
– детерминированный матричный оператор; 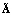 – стохастический матричный оператор; Cx и Cy – проекционные характеристики выходного сигнала x и входного сигнала y соответственно, представляющие собой вектор-столбцы коэффициентов разложения данных сигналов по ортогональному базису
– стохастический матричный оператор; Cx и Cy – проекционные характеристики выходного сигнала x и входного сигнала y соответственно, представляющие собой вектор-столбцы коэффициентов разложения данных сигналов по ортогональному базису
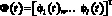 ,
,
где 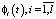 – элементы системы ортонормированных функций, в качестве которой в настоящей статье используется система функций Уолша; T – знак транспонирования.
– элементы системы ортонормированных функций, в качестве которой в настоящей статье используется система функций Уолша; T – знак транспонирования.
Матричные операторы 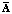 и
и 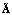 определяются следующим образом:
определяются следующим образом:
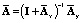 ,
, 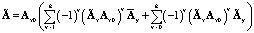 ,
,
где 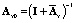 ;
; 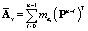 ;
; 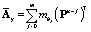 ;
; 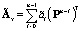 ,
, 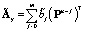 ; P – матричный оператор интегрирования в базисе функций Уолша [3].
; P – матричный оператор интегрирования в базисе функций Уолша [3].
Выражение (4) позволяет определить проекционные характеристики математического ожидания и корреляционной функции выходного сигнала стохастической системы следующим образом:
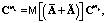 (5)
(5)
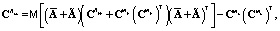 (6)
(6)
где 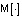 – оператор математического ожидания, применяемый с учетом предположения о статистической независимости сигнала y и случайных коэффициентов ai, bj. При этом проекционные характеристики математического ожидания my(t) и корреляционной функции Ryy(t1, t2) входного сигнала на интервале исследования [0, T] определяются соответственно как
– оператор математического ожидания, применяемый с учетом предположения о статистической независимости сигнала y и случайных коэффициентов ai, bj. При этом проекционные характеристики математического ожидания my(t) и корреляционной функции Ryy(t1, t2) входного сигнала на интервале исследования [0, T] определяются соответственно как
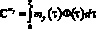 ;
;
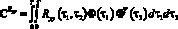 .
.
Выражения (5) и (6) являются формальным представлением усредненной проекционной модели системы (1). Чтобы воспользоваться этими соотношениями для решения задачи статистического анализа стохастических систем, необходимо выполнить операцию усреднения 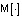 . Представление стохастического матричного оператора
. Представление стохастического матричного оператора 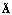 в виде ряда Неймана, как это показано выше, позволяет выделить стохастические моменты произведений различных степеней случайных величин
в виде ряда Неймана, как это показано выше, позволяет выделить стохастические моменты произведений различных степеней случайных величин 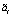 ,
, 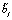 . Вычисление этих моментов сводится к аналитическому усреднению указанных случайных величин, возведенных в соответствующие степени, то есть к вычислению моментов соответствующих порядков, что может быть сделано с помощью известного соотношения, которое является тождеством по λ и устанавливает связь между начальными моментами αr и кумулянтами (семиинвариантами) αr скалярной случайной величины [7]:
. Вычисление этих моментов сводится к аналитическому усреднению указанных случайных величин, возведенных в соответствующие степени, то есть к вычислению моментов соответствующих порядков, что может быть сделано с помощью известного соотношения, которое является тождеством по λ и устанавливает связь между начальными моментами αr и кумулянтами (семиинвариантами) αr скалярной случайной величины [7]:
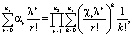
где n1 – порядок момента, выражаемого через кумулянты порядка до n2 включительно. Для гауссовых случайных величин (n2 = 2) первый кумулянт в точности соответствует математическому ожиданию, а второй – дисперсии, и стохастический момент любого порядка n1 выше второго определяется через эти статистические характеристики. При этом все кумулянты старше второго равны нулю, поэтому для гауссовых 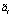 ,
, 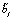 в (2), центрированных по определению, достаточно задать только их дисперсии
в (2), центрированных по определению, достаточно задать только их дисперсии 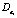 ,
, 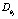 . Для негауссовых случайных величин стохастический момент порядка выше второго выражается не только через первый и второй кумулянты, но и через более старшие. Поэтому для таких случайных величин (негауссовых
. Для негауссовых случайных величин стохастический момент порядка выше второго выражается не только через первый и второй кумулянты, но и через более старшие. Поэтому для таких случайных величин (негауссовых 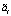 ,
, 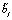 ) необходимо задать то число кумулянтов, которое требуется для достижения заданной точности представления негауссового закона распределения с учетом факта уменьшения значимости кумулянта с увеличением его номера. Для некоторых законов распределения стохастические моменты вычисляются проще. Например, для непрерывного равномерного распределения на отрезке [a, b] момент n-го порядка определяется известной формулой
) необходимо задать то число кумулянтов, которое требуется для достижения заданной точности представления негауссового закона распределения с учетом факта уменьшения значимости кумулянта с увеличением его номера. Для некоторых законов распределения стохастические моменты вычисляются проще. Например, для непрерывного равномерного распределения на отрезке [a, b] момент n-го порядка определяется известной формулой
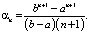
Из (5) и (6) следует вывод об аддитивном характере влияния фактора случайности параметров стохастической системы на статистические характеристики ее выходного сигнала, то есть
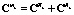 ,
, 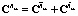 ,
,
где
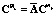 ;
; 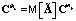 ;
; 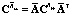 ;
; 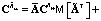
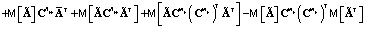 .
.
Проекционные характеристики 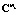 и
и 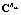 позволяют приближенно восстановить функции математического ожидания mx(t) и корреляции Rxx(t1, t2). Тогда в случае использования ортогонального базиса функций Уолша результатом статистического анализа модели (1) будет соответственно вектор-столбец дискретных значений (отсчетов) функции
позволяют приближенно восстановить функции математического ожидания mx(t) и корреляции Rxx(t1, t2). Тогда в случае использования ортогонального базиса функций Уолша результатом статистического анализа модели (1) будет соответственно вектор-столбец дискретных значений (отсчетов) функции 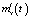 размерности l и квадратная матрица отсчетов функции
размерности l и квадратная матрица отсчетов функции 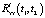 размерности l×l:
размерности l×l:
 (7)
(7)
 (8)
(8)
Таким образом, из (8) следует, что корреляционная функция выходного сигнала стохастической системы 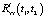 может быть представлена как сумма корреляционной функции выходного сигнала эквивалентной детерминированной системы
может быть представлена как сумма корреляционной функции выходного сигнала эквивалентной детерминированной системы 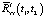 , модель которой также описывается уравнением (1), где случайные коэффициенты ai, bj заменены своими средними значениями
, модель которой также описывается уравнением (1), где случайные коэффициенты ai, bj заменены своими средними значениями 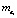 ,
, 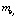 , и составляющей
, и составляющей 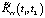 , наличие которой отражает влияние фактора случайности параметров стохастической системы. На основе соотношения (8) строится рассматриваемый далее алгоритм компенсации данного фактора. Аналогичный вывод следует из (7), где наличие составляющей
, наличие которой отражает влияние фактора случайности параметров стохастической системы. На основе соотношения (8) строится рассматриваемый далее алгоритм компенсации данного фактора. Аналогичный вывод следует из (7), где наличие составляющей 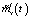 подчеркивает тот факт, что математическое ожидание выходного сигнала стохастической системы
подчеркивает тот факт, что математическое ожидание выходного сигнала стохастической системы 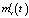 не равно математическому ожиданию выходного сигнала эквивалентной детерминированной системы
не равно математическому ожиданию выходного сигнала эквивалентной детерминированной системы 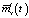 . Наличие составляющей
. Наличие составляющей 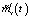 обусловлено неизбежной корреляцией выходного сигнала стохастической системы и случайных коэффициентов ai левой части уравнения (1), поэтому усредненную модель такой системы нельзя получить простой заменой случайных коэффициентов ai, bj их средними значениями.
обусловлено неизбежной корреляцией выходного сигнала стохастической системы и случайных коэффициентов ai левой части уравнения (1), поэтому усредненную модель такой системы нельзя получить простой заменой случайных коэффициентов ai, bj их средними значениями.
Также следует отметить, что соотношения (7) и (8) справедливы при условии, что справедливы соотношения (5) и (6), в которых матричный оператор стохастической системы представлен как 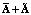 . Такое представление, в свою очередь, требует, чтобы матричный ряд Неймана, аппроксимирующий стохастический оператор
. Такое представление, в свою очередь, требует, чтобы матричный ряд Неймана, аппроксимирующий стохастический оператор 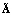 , после своего почленного усреднения сходился для выбранного числа удерживаемых членов k. Возможность почленного усреднения данного ряда для соотношения (5) обоснована тем, что вследствие абсолютной сходимости ряда Неймана можно поменять местами операторы суммирования и математического ожидания. Что касается соотношения (6), то для обоснования правомочности почленного усреднения двойного ряда
, после своего почленного усреднения сходился для выбранного числа удерживаемых членов k. Возможность почленного усреднения данного ряда для соотношения (5) обоснована тем, что вследствие абсолютной сходимости ряда Неймана можно поменять местами операторы суммирования и математического ожидания. Что касается соотношения (6), то для обоснования правомочности почленного усреднения двойного ряда 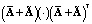 можно при весьма общих предположениях сослаться на теорему Фубини. Заметим, что вышеупомянутые усредненные ряды являются полусходящимися, то есть сходятся только до определенного k. Условия их сходимости, связывающие число k с дисперсиями собственных значений случайной матрицы
можно при весьма общих предположениях сослаться на теорему Фубини. Заметим, что вышеупомянутые усредненные ряды являются полусходящимися, то есть сходятся только до определенного k. Условия их сходимости, связывающие число k с дисперсиями собственных значений случайной матрицы 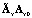 , можно найти в [7]. Вопросы сходимости и точности проекционных аппроксимаций с применением техники матричных операторов подробно рассмотрены в монографии [3].
, можно найти в [7]. Вопросы сходимости и точности проекционных аппроксимаций с применением техники матричных операторов подробно рассмотрены в монографии [3].
Принцип компенсации случайности параметров
Активная компенсация случайности параметров стохастической системы осуществляется подачей на ее вход скорректированного управляющего воздействия в виде специально сформированного случайного процесса, обеспечивающего получение таких статистических характеристик выходного сигнала, которые имел бы выходной сигнал эквивалентной детерминированной системы при подаче на ее вход нескорректированного управляющего воздействия. Иными словами, активная компенсация может при определенных условиях заставить стохастическую систему вести себя подобно детерминированной при отработке особым образом сформированного случайного управляющего воздействия, нивелирующего влияние фактора случайности ее параметров. Далее рассмотрим метод активной компенсации, обеспечивающий приближение 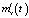 и
и 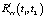 к
к 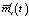 и
и 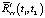 соответственно.
соответственно.
Задача компенсации по математическому ожиданию может быть сведена к решению обратной задачи динамики в статистической постановке, то есть к нахождению математического ожидания скорректированного входного сигнала стохастической системы 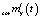 по заданному
по заданному 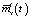 . Соотношение (5) позволяет при определенных условиях решить данную обратную задачу в смысле определения проекционной характеристики
. Соотношение (5) позволяет при определенных условиях решить данную обратную задачу в смысле определения проекционной характеристики 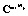 функции
функции 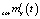 по заданной проекционной характеристике
по заданной проекционной характеристике 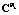 функции
функции 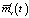 . Для этого введем понятие усредненного матричного оператора стохастической системы, представляющего собой матрицу математического ожидания стохастического оператора
. Для этого введем понятие усредненного матричного оператора стохастической системы, представляющего собой матрицу математического ожидания стохастического оператора 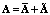 :
:
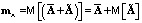 .
.
Тогда, предполагая обратимость матрицы 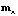 , можно записать следующее соотношение:
, можно записать следующее соотношение:
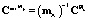 ,
,
которое, однако, является формальным в том смысле, что не позволяет решить сформулированную в таком виде обратную задачу на практике вследствие того, что оператор 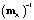 фактически является дифференциальным оператором, соответствующим физически нереализуемой системе. Обойти данную проблему можно, обратившись к понятию реального дифференцирующего звена, используемому в подобных случаях в теории управления. Данное звено описывается дифференциальным уравнением
фактически является дифференциальным оператором, соответствующим физически нереализуемой системе. Обойти данную проблему можно, обратившись к понятию реального дифференцирующего звена, используемому в подобных случаях в теории управления. Данное звено описывается дифференциальным уравнением 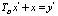 , которому соответствует проекционная модель
, которому соответствует проекционная модель 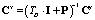 , где матрица
, где матрица 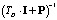 представляет собой матричный оператор реального дифференцирующего звена (реальный оператор дифференцирования), в то время как просто матричный оператор дифференцирования определяется как P–1. Постоянная времени TD выбирается достаточно малой, но такой, чтобы не нарушать условий физической реализуемости выходного сигнала дифференцирующего звена в контексте конкретной прикладной задачи.
представляет собой матричный оператор реального дифференцирующего звена (реальный оператор дифференцирования), в то время как просто матричный оператор дифференцирования определяется как P–1. Постоянная времени TD выбирается достаточно малой, но такой, чтобы не нарушать условий физической реализуемости выходного сигнала дифференцирующего звена в контексте конкретной прикладной задачи.
Вычисляя матричные операторы 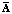 и
и 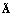 по приведенным ранее формулам, в которых оператор интегрирования P заменен оператором
по приведенным ранее формулам, в которых оператор интегрирования P заменен оператором 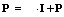 , можно вычислить оператор
, можно вычислить оператор 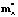 , заменяющий оператор mA в вышеприведенном формальном соотношении и в конечном итоге вычислить искомое математическое ожидание скорректированного входного сигнала стохастической системы:
, заменяющий оператор mA в вышеприведенном формальном соотношении и в конечном итоге вычислить искомое математическое ожидание скорректированного входного сигнала стохастической системы:
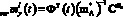 . (9)
. (9)
Следующим этапом является определение корреляционной функции скорректированного входного сигнала, которую обозначим как 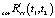 . Заметим, что вследствие очевидной невозможности представить усредненную матрицу
. Заметим, что вследствие очевидной невозможности представить усредненную матрицу 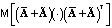 в (6) в виде произведения двух усредненных матриц
в (6) в виде произведения двух усредненных матриц 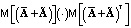 данная задача не может быть решена простым инвертированием прямой задачи, как это было сделано при определении
данная задача не может быть решена простым инвертированием прямой задачи, как это было сделано при определении 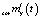 . Вместо этого можно обратиться к соотношению (8), из которого следует, что для компенсации его второго слагаемого
. Вместо этого можно обратиться к соотношению (8), из которого следует, что для компенсации его второго слагаемого 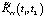 можно заменить первое слагаемое
можно заменить первое слагаемое 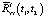 на функцию
на функцию 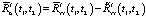 , которая представляет собой измененную корреляционную функцию выходного сигнала эквивалентной детерминированной системы, устраняющую при определенных условиях влияние
, которая представляет собой измененную корреляционную функцию выходного сигнала эквивалентной детерминированной системы, устраняющую при определенных условиях влияние 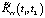 на корреляционную функцию выходного сигнала стохастической системы
на корреляционную функцию выходного сигнала стохастической системы 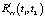 , то есть
, то есть
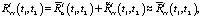 (10)
(10)
где скорректированную корреляционную функцию выхода эквивалентной детерминированной системы можно также определить как
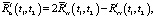 (11)
(11)
то есть без необходимости отдельного вычисления 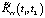 . При этом как
. При этом как 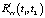 в (11), так и
в (11), так и 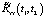 в (10) вычисляются при
в (10) вычисляются при 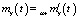 , то есть предполагается, что компенсация по математическому ожиданию уже выполнена.
, то есть предполагается, что компенсация по математическому ожиданию уже выполнена.
Естественно, что при вышеописанном подходе компенсация возможна, только если не нарушается условие положительной определенности функции 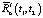 . Иными словами, должен иметься достаточный «резерв по дисперсии» выходного сигнала эквивалентной детерминированной системы
. Иными словами, должен иметься достаточный «резерв по дисперсии» выходного сигнала эквивалентной детерминированной системы 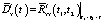 .
.
Корреляционная функция скорректированного входного сигнала может быть найдена в результате решения следующей обратной задачи для эквивалентной детерминированной системы:
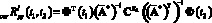 , (12)
, (12)
где 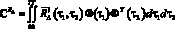 ; P* – матричный оператор, вычисляемый с использованием оператора интегрирования
; P* – матричный оператор, вычисляемый с использованием оператора интегрирования 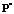 , как это делалось выше для матричного оператора
, как это делалось выше для матричного оператора  . При этом постоянная времени TD также выбирается достаточно малой, но такой, чтобы не нарушалось условие положительной определенности найденной функции
. При этом постоянная времени TD также выбирается достаточно малой, но такой, чтобы не нарушалось условие положительной определенности найденной функции 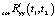 .
.
Следует сделать одно замечание, касающееся приближенного равенства (10). Данное равенство в принципе не может быть точным, то есть полная компенсация по корреляционной функции не может быть достигнута таким способом, так как 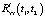 в соотношении (11) определяется для нескорректированной корреляционной функции входного сигнала Ryy(t1, t2), в то время как
в соотношении (11) определяется для нескорректированной корреляционной функции входного сигнала Ryy(t1, t2), в то время как 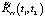 в соотношении (10) определяется для скорректированной
в соотношении (10) определяется для скорректированной 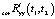 . Однако на практике вклад корреляционной функции входного сигнала в корреляционную функцию выходного сигнала стохастической системы обычно значительно меньше, чем вклад, вносимый его ненулевым математическим ожиданием. Это объясняется тем, что система управления обычно отрабатывает пусть и зашумленный, но в среднем детерминированный полезный сигнал (математическое ожидание входного случайного процесса), и амплитуда изменения этого полезного сигнала часто существенно превышает амплитуду случайной аддитивной помехи.
. Однако на практике вклад корреляционной функции входного сигнала в корреляционную функцию выходного сигнала стохастической системы обычно значительно меньше, чем вклад, вносимый его ненулевым математическим ожиданием. Это объясняется тем, что система управления обычно отрабатывает пусть и зашумленный, но в среднем детерминированный полезный сигнал (математическое ожидание входного случайного процесса), и амплитуда изменения этого полезного сигнала часто существенно превышает амплитуду случайной аддитивной помехи.
Улучшить результат компенсации по корреляционной функции на основе соотношений (10), (11) можно, если использовать метод последовательных приближений в той или иной форме. Например, принимая нескорректированную корреляционную функцию Ryy(t1, t2) за нулевое приближение, найти первое приближение 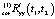 , обеспечивающее приближенное равенство (10). Далее, принимая
, обеспечивающее приближенное равенство (10). Далее, принимая 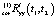 за Ryy(t1, t2) и повторяя алгоритм компенсации, найти второе приближение
за Ryy(t1, t2) и повторяя алгоритм компенсации, найти второе приближение 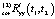 и т.д.
и т.д.
Найденные статистические характеристики скорректированного входного сигнала используются при формировании случайного процесса, представляющего данный сигнал в практических приложениях. Для этого могут быть применены различные известные методы, например в [7] описан метод формирования случайных процессов, включая нестационарные, основанный на каноническом разложении, в котором переход к системе некоррелированных случайных величин осуществляется с использованием алгоритма ортогонализации на основе разложения Холецкого.
Алгоритм компенсации
Данный алгоритм строится на основе вышеописанного принципа активной компенсации и включает выполнение следующих основных шагов:
1. Решается задача статистического анализа для модели эквивалентной детерминированной системы с использованием следующих соотношений:
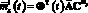 ;
;
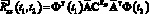 .
.
2. Вычисляется математическое ожидание скорректированного входного сигнала 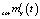 для модели стохастической системы с использованием соотношения (9). При этом минимальное значение постоянной времени TD выбирается из условия физической реализуемости скорректированного входного сигнала.
для модели стохастической системы с использованием соотношения (9). При этом минимальное значение постоянной времени TD выбирается из условия физической реализуемости скорректированного входного сигнала.
3. Вычисляется корреляционная функция выходного сигнала 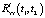 для модели стохастической системы с использованием соотношения (8), где составляющая
для модели стохастической системы с использованием соотношения (8), где составляющая 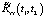 вычисляется при
вычисляется при 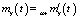 , то есть математическое ожидание входного сигнала полагается скорректированным, в то время как его корреляционная функция Ryy(t1, t2) та же, что на шаге 1.
, то есть математическое ожидание входного сигнала полагается скорректированным, в то время как его корреляционная функция Ryy(t1, t2) та же, что на шаге 1.
4. Вычисляется скорректированная корреляционная функция выхода эквивалентной детерминированной системы с помощью соотношения (11), записанного в форме
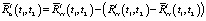 .
.
Как показывает практика, последнее соотношение целесообразно модифицировать следующим образом:
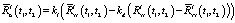 , (13)
, (13)
где коэффициенты kl ≤ 1 и kd ≤ 1 определяют соответственно уровень и глубину компенсации, позволяя достичь компромисса между стремлением, с одной стороны, минимизировать TD для обеспечения максимально возможной точности решения обратной задачи с одновременным соблюдением условия физической реализуемости скорректированного входного сигнала, а с другой – удовлетворить требованию положительной определенности функции 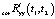 , вычисляемой на следующем шаге.
, вычисляемой на следующем шаге.
5. Вычисляется скорректированная корреляционная функция 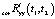 с использованием соотношения (12). При этом может потребоваться подбор соответствующих значений коэффициентов kl, kd в соотношении (13) и постоянной времени TD, используемой при вычислении матрицы
с использованием соотношения (12). При этом может потребоваться подбор соответствующих значений коэффициентов kl, kd в соотношении (13) и постоянной времени TD, используемой при вычислении матрицы 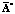 в (12).
в (12).
Для определения значений kl, kd, TD при выполнении шагов 4 и 5 описанного алгоритма можно воспользоваться процедурой минимизации следующего функционала, определяющего меру близости проекционных характеристик корреляционной функции выходного сигнала стохастической системы 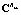 и эквивалентной детерминированной системы
и эквивалентной детерминированной системы 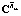 :
:
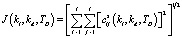 ,
,
где 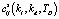 – элементы матрицы
– элементы матрицы 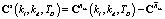 . Данный функционал минимизируется при вышеупомянутых ограничениях на значения kl, kd, TD, гарантирующих возможность формирования скорректированного входного сигнала в виде случайного процесса с заданными статистическими характеристиками.
. Данный функционал минимизируется при вышеупомянутых ограничениях на значения kl, kd, TD, гарантирующих возможность формирования скорректированного входного сигнала в виде случайного процесса с заданными статистическими характеристиками.
Для формирования скорректированного входного сигнала в виде случайного процесса с найденными характеристиками 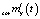 и
и 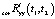 может быть использован упомянутый ранее метод на основе канонического разложения, описанный в [7].
может быть использован упомянутый ранее метод на основе канонического разложения, описанный в [7].
Пример активной компенсации случайности параметров
В качестве примера рассмотрим решение задачи компенсации влияния случайности физических параметров электрогидравлического следящего привода (ЭГСП) виброиспытательного стенда на статистические характеристики воспроизводимого вибрационного воздействия, прикладываемого к испытываемому изделию. Проблема состоит в том, что из-за нестабильности параметров ЭГСП, обусловленной как внешними (температура окружающей среды), так и внутренними (содержание газовой фазы в рабочей жидкости) случайными факторами, имеет место искажение упомянутых статистических характеристик. Таким образом, ЭГСП следует рассматривать как стохастическую систему со всеми особенностями ее поведения. В частности, как следует из соотношений (5)–(8), корреляционная функция выходного сигнала стохастической системы определяется не только корреляционной функцией входного сигнала, как это имеет место для детерминированной системы, но и математическим ожиданием данного сигнала, что приводит к искажению этой корреляционной функции при воспроизведении случайного вибрационного воздействия с ненулевым математическим ожиданием. Это может привести к снижению качества вибрационных испытаний и получению неадекватных результатов в случаях, когда требуется обеспечить точное соответствие формируемых вибрационных воздействий некоторым реальным. Задача компенсации состоит в нахождении таких статистических характеристик сигнала, подаваемого на вход ЭГСП со случайными параметрами, которые обеспечивали бы статистические характеристики воспроизводимого вибрационного воздействия, максимально приближенные к статистическим характеристикам выходного сигнала ЭГСП с неслучайными параметрами. Данная задача решалась в рамках вычислительного эксперимента в среде системы MATLAB® (The MathWorks Inc.).
Рассматриваемый ЭГСП описывается моделью (1), где n = 5 и m = 0, построенной на основе типовой линеаризованной модели ЭГСП, представляющий собой редуцированный вариант модели, описанной в [2], или более подробно – в [6]. Начальные условия полагаются нулевыми, то есть компенсация будет выполняться для переходного режима работы ЭГСП. Случайный физический параметр – коэффициент вязкого трения на золотнике электрогидравлического усилителя, обозначаемый как hз и имеющий размерность 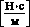 . Данный параметр является гауссовой случайной величиной с математическим ожиданием
. Данный параметр является гауссовой случайной величиной с математическим ожиданием 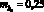 и дисперсией
и дисперсией 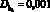 . При этом в уравнении (1) случайными будут коэффициенты a1, a2, a3, a4, математические ожидания и дисперсии которых определяются через заданные
. При этом в уравнении (1) случайными будут коэффициенты a1, a2, a3, a4, математические ожидания и дисперсии которых определяются через заданные  и
и 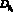 . В качестве ортогонального базиса Ф(t) используется базис функций Уолша с
. В качестве ортогонального базиса Ф(t) используется базис функций Уолша с 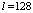 . В матричном ряду, аппроксимирующем стохастический оператор
. В матричном ряду, аппроксимирующем стохастический оператор  , удерживаются первые два члена (k = 2). Усреднение проекционной модели (5), (6) выполняется с учетом наличия жесткой статистической связи между случайными коэффициентами уравнения (1), обусловленной их общей зависимостью от hз.
, удерживаются первые два члена (k = 2). Усреднение проекционной модели (5), (6) выполняется с учетом наличия жесткой статистической связи между случайными коэффициентами уравнения (1), обусловленной их общей зависимостью от hз.
На задающий вход электронного усилителя сигнала ошибки (входной сигнал ЭГСП) поступает сигнал в виде случайного процесса с математическим ожиданием 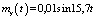 и корреляционной функцией
и корреляционной функцией 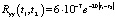 . Корреляционная функция выходного сигнала
. Корреляционная функция выходного сигнала 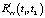 представлена на рис. 1, где хорошо видны колебания дисперсии
представлена на рис. 1, где хорошо видны колебания дисперсии 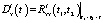 с двойной частотой изменения my(t).
с двойной частотой изменения my(t).
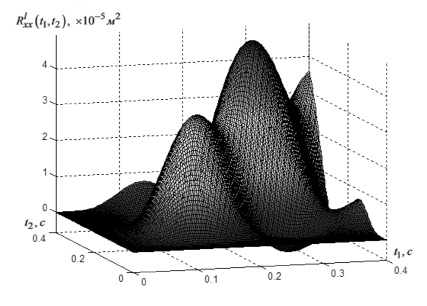
Рис. 1. Корреляционная функция выходного сигнала стохастической модели ЭГСП до компенсации случайности параметра hз
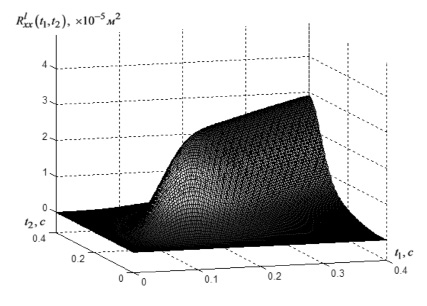
Рис. 2. Корреляционная функция выходного сигнала эквивалентной детерминированной модели ЭГСП
Корреляционная функция выходного сигнала эквивалентной детерминированной системы 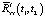 , представленная на рис. 2, не имеет таких колебаний, и дисперсия данного сигнала, соответственно, изменяется по апериодическому закону, достигая некоторого установившегося значения.
, представленная на рис. 2, не имеет таких колебаний, и дисперсия данного сигнала, соответственно, изменяется по апериодическому закону, достигая некоторого установившегося значения.
В рассматриваемом примере наибольшее искажение, вызванное влиянием случайности параметров системы, наблюдается у корреляционной функции, в то время как искажение математического ожидания незначительно, поэтому его графики не приводятся, но тем не менее, согласно (5) и (7), это искажение всегда имеет место.
Решая задачу активной компенсации случайности параметра hз в соответствии с описанным выше алгоритмом, на шаге 2, выбирая TD = 5•10–4, находим математическое ожидание скорректированного входного сигнала 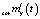 , которое используется на шаге 3 для вычисления
, которое используется на шаге 3 для вычисления 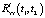 . График данной корреляционной функции мало отличается от представленного на рис. 1, поэтому здесь не приводится.
. График данной корреляционной функции мало отличается от представленного на рис. 1, поэтому здесь не приводится.
Выполняя шаги 4 и 5, находим 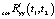 . При этом выбираем
. При этом выбираем 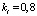 ,
, 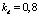 , TD = 7•10–3. Результат компенсации представлен на рис. 3, где показана корреляционная функция выходного сигнала стохастической модели ЭГСП, вычисленная для скорректированного входного сигнала в виде случайного процесса с найденными характеристиками
, TD = 7•10–3. Результат компенсации представлен на рис. 3, где показана корреляционная функция выходного сигнала стохастической модели ЭГСП, вычисленная для скорректированного входного сигнала в виде случайного процесса с найденными характеристиками 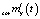 и
и 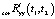 .
.
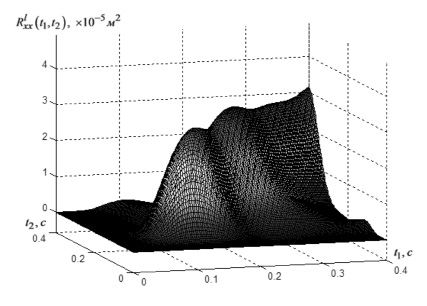
Рис. 3. Корреляционная функция выходного сигнала стохастической модели ЭГСП после компенсации случайности параметра hз
За исключением небольших колебаний дисперсии 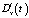 , график рис. 3 близок к графику корреляционной функции выходного сигнала эквивалентной детерминированной системы рис. 2, со значением дисперсии в установившемся режиме около 3•10–5. Имеющиеся отличия объясняются принципиально приближенным характером равенства (10) и неточностью вычисления
, график рис. 3 близок к графику корреляционной функции выходного сигнала эквивалентной детерминированной системы рис. 2, со значением дисперсии в установившемся режиме около 3•10–5. Имеющиеся отличия объясняются принципиально приближенным характером равенства (10) и неточностью вычисления 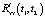 на шаге 3 из-за удержания ограниченного числа членов матричного ряда, аппроксимирующего стохастический оператор
на шаге 3 из-за удержания ограниченного числа членов матричного ряда, аппроксимирующего стохастический оператор  .
.
Заметим, что величина дисперсии случайного физического параметра hз принята несколько завышенной по сравнению с тем, что обычно имеет место на практике. Это сделано с целью более наглядной демонстрации эффективности предлагаемого метода активной компенсации, дающего удовлетворительный результат даже при столь значительном искажении корреляционной функции выходного сигнала, вызванном случайностью данного параметра.
Заключение
Использование усредненных проекционных моделей стохастических систем позволило предложить новый подход к активной компенсации случайности физических параметров систем управления, идея которого следует из операторной формы этих моделей.
Компенсация по математическому ожиданию достигается путем обращения усредненного стохастического матричного оператора (усредненной проекционной характеристики стохастической системы), вычисляемого с использованием матричного оператора реального дифференцирующего звена. Возможность такого обращения позволяет решить обратную задачу динамики в статистической постановке, благодаря чему удается найти такое математическое ожидание случайного процесса, поступающего на вход стохастической системы, которое обеспечивает требуемое математическое ожидание случайного процесса на ее выходе, компенсируя искажение данной статистической характеристики, вызванное случайностью параметров системы.
Принцип компенсации по корреляционной функции основан на возможности представить корреляционную функцию случайного процесса на выходе стохастической системы как сумму двух составляющих – корреляционной функции на выходе эквивалентной детерминированной системы и составляющей, обусловленной влиянием случайности параметров системы. Выполняя обращение матричного оператора эквивалентной детерминированной системы, также вычисляемого с использованием матричного оператора реального дифференцирующего звена, можно при определенных условиях найти такую корреляционную функцию случайного процесса на входе стохастической системы, которая нивелирует вторую вышеупомянутую составляющую корреляционной функции ее выходного сигнала.
На примере активной компенсации влияния случайности физических параметров электрогидравлического следящего привода виброиспытательного стенда показано, что можно заметно улучшить точность воспроизведения статистических характеристик формируемого вибрационного воздействия.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Калужской области (проект № 16-41-400701).
Библиографическая ссылка
Макаренков А.М., Тун Тун Чжо, Тин Эй Чжо, Мьо Паинг Сат АКТИВНАЯ КОМПЕНСАЦИЯ СЛУЧАЙНОСТИ ПАРАМЕТРОВ СТОХАСТИЧЕСКИХ СИСТЕМ // Фундаментальные исследования. – 2017. – № 4-1. – С. 54-63;URL: https://fundamental-research.ru/ru/article/view?id=41435 (дата обращения: 20.04.2024).



