Сегодня Республику Дагестан трудно представить без виноградарства и виноделия и они по праву считаются ведущими отраслями сельского хозяйства. На этот регион приходится 40 % виноградных насаждений, производится более 65 % столового винограда страны, по рейтинговой оценке это второе место после Краснодарского края. Условия республики позволяют сформировать непрерывный «конвейер» производства винограда столовых и технических сортов разных сроков созревания, это способствует развитию инфраструктуры сбыта продукции.
Общая площадь виноградников в России в 2016 г. составила более 85 тыс. гектаров. Из них на Дагестан приходится 21 тыс. гектаров. С 2013 г. в рамках приоритетного проекта развития РД «Эффективный АПК» поставлена задача ежегодно увеличивать площади виноградников на 2 тыс. га. В 2016 г. план по закладке новых кустов солнечной ягоды установлен в объеме 2 070 га. Для обеспечения виноградарей собственным виноградным посадочным материалом в республике выращены около 2 млн штук сертифицированных саженцев требуемого сортового состава.
В настоящее время выращиванием винограда в РД занимаются более 97 хозяйств всех категорий, в том числе 47 специализированных, из них 17 имеют заводы первичного виноделия, 20 предприятий осуществляют розлив винодельческой продукции.
Целью настоящего исследования является разработка эконометрических моделей для анализа и прогнозирования основных производственно-экономических показателей предприятий сельского хозяйства Республики Дагестан.
Эконометрический анализ по группам сельскохозяйственных предприятий позволяет дать полную и всестороннюю характеристику состояния сельского хозяйства региона, установить закономерности его развития, что создает научную основу для планирования и прогнозирования экономических процессов [1].
Исследование проведено на основе корреляционно-регрессионного анализа в сочетании с трендовым моделированием. При этом в процессе прогнозирования отбирают наиболее значимые факторы, определяют степень их участия в формировании результативного показателя.
Для этого выбраны крупные сельскохозяйственные предприятия Республики Дагестан по производству винограда: ГУП «Каспий», ГУП «Кировский», ГУП «Каякентский».
Основные производственно-экономические показатели сельскохозяйственных предприятий Республики Дагестан представлены в табл. 1.
Таблица 1
Основные производственно-экономические показатели сельскохозяйственных предприятий Республики Дагестан за 2010–2015 гг.
|
Выручка от реализации винограда, тыс. руб. |
Затраты на производство в растениеводстве, тыс. руб. |
Затраты на уход за молодыми виноградниками, тыс. руб. |
Урожайность винограда, ц\га |
|||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
|
2010 |
61112 |
58809 |
26689 |
55292 |
59438 |
44514 |
3340 |
5455 |
4826 |
107,8 |
142,2 |
42,2 |
|
2011 |
58837 |
69094 |
31745 |
65942 |
62146 |
38849 |
2055 |
4100 |
3935 |
112,3 |
146,4 |
43,6 |
|
2012 |
20962 |
10729 |
15384 |
54680 |
26422 |
31265 |
4496 |
3806 |
3630 |
45,9 |
21,1 |
24,2 |
|
2013 |
55437 |
57532 |
39094 |
67888 |
56364 |
57603 |
2900 |
3186 |
2581 |
112,1 |
119,3 |
58,8 |
|
2014 |
51343 |
51480 |
30324 |
65023 |
50221 |
44502 |
2683 |
6550 |
4012 |
102,3 |
102,5 |
51,6 |
|
2015 |
59010 |
56710 |
44272 |
68187 |
43653 |
48966 |
2954 |
5002 |
2902 |
109,5 |
91,7 |
53,3 |
Примечание. 1 – ГУП «Каспий», 2 – ГУП «Кировский», 3 – ГУП «Каякентский».
Ряды динамики – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Отдельные наблюдения, из которых состоят ряды динамики, называются уровнями этого рядя и обозначаются Yt, где t = 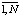 . Таким образом, обязательные элементы ряда динамики – это показатели времени t и уровни ряда y [1, 3, 4].
. Таким образом, обязательные элементы ряда динамики – это показатели времени t и уровни ряда y [1, 3, 4].
По данным табл. 1 построены модели рядов динамики. Для ГУП «Каспий» модель имеет следующий вид:
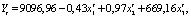
(R2 =0,99), (1)
где Yt – это выручка от реализации винограда, 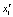 – затраты на производство в растениеводстве,
– затраты на производство в растениеводстве,  – затраты на уход за молодыми виноградниками,
– затраты на уход за молодыми виноградниками, 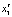 – урожайность винограда.
– урожайность винограда.
R2 – индекс детерминации. Индекс детерминации – это квадрат индекса корреляции. Этим значением характеризуют, на какое количество процентов моделью регрессии объясняются варианты показателей результативной переменной по отношению к своему среднему уровню.
Для ГУП «Кировский» модель имеет вид
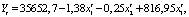
(R2 =0,91). (2)
Для ГУП «Каякентский» модель имеет вид:
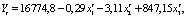
(R2 =0,86). (3)
Для того чтобы рассчитать прогнозы выручки от реализации винограда по модели рядов динамики, необходимо определить прогнозные значения показателей-факторов модели. Они рассчитаны по следующим моделям:
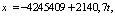
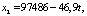
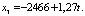
Прогнозные значения затрат на производство в растениеводстве, затрат на уход за молодыми виноградниками, урожайности винограда предприятий Республики Дагестан, рассчитанные по линейному тренду, представлены в табл. 2.
Таблица 2
Прогнозные значения затрат на производство в растениеводстве, затрат на уход за молодыми виноградниками, урожайности винограда предприятий Республики Дагестан, рассчитанные по данным за 2010–2015 гг.
|
ГУП |
x1 |
x2 |
x3 |
||||||
|
2016 |
2017 |
2018 |
2016 |
2017 |
2018 |
2016 |
2017 |
2018 |
|
|
Каспий |
70327,9 |
72468,7 |
74609,4 |
2907,1 |
2860,2 |
2813,3 |
102,8 |
104 |
105,3 |
|
Кировский |
41231,5 |
38809,9 |
36388,2 |
5129,7 |
5257,2 |
5384,8 |
75,3 |
67,1 |
58,9 |
|
Каякентский |
50838,9 |
52711,9 |
54585 |
2603,9 |
2305,6 |
2007,4 |
57 |
60,3 |
63,5 |
Таблица 3
Прогнозные значения выручки от реализации винограда предприятий Республики Дагестан, полученные по моделям рядов динамики, тыс. руб.
|
ГУП «Каспий» |
ГУП «Кировский» |
ГУП «Каякентский» |
|||||||
|
2016 |
2017 |
2018 |
2016 |
2017 |
2018 |
2016 |
2017 |
2018 |
|
|
С учетом 2012 г. |
50753 |
50649 |
50545 |
38945 |
35579 |
32213 |
42271 |
45420 |
48568 |
|
Без 2012 г. |
53053 |
51848 |
50644 |
50601 |
47893 |
45185 |
42123 |
44690 |
47256 |
Прогнозные значения выручки от реализации винограда, полученные по моделям (1)–(3), представлены в первой строке табл. 3.
Сильные заморозки 2012 г. оказали негативное воздействие на деятельность сельскохозяйственных предприятий РД. По этой причине в этом году имела место значительная деградация рассматриваемых показателей, по сравнению с остальными уровнями временного ряда. Известно, что любая изучаемая совокупность может содержать единицы наблюдения, значения признаков которых резко выделяются из основной массы значений. Такие нетипичные значения признаков (выбросы) нарушают статистическую закономерность изучаемого явления [2, 4, 5]. Следовательно, аномальные наблюдения могут не только исказить значения обобщающих показателей (средней, дисперсии, среднего квадратического отклонения и др.), но и привести к серьезным ошибкам в прогнозах, полученных по построенным моделям. В связи с этим обозначилась необходимость построения моделей рядов динамики по данным, не содержащим аномальные значения. Прогнозы по ним представлены во второй строке табл. 3.
Сравним основные статистические характеристики полученных моделей на примере ГУП «Каспий». Выручка от реализации винограда фактическая (2010–2015 гг.) и прогнозные значения на 2016–2018 гг. ГУП «Каспий» по различным моделям графически представлены на рисунке.
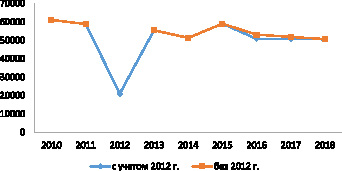
Выручка от реализации винограда фактическая (2010–2015 гг.) и прогнозные значения на 2016–2018 гг. ГУП «Каспий» по различным моделям
Как видно на графике, прогноз выручки от реализации винограда в 2018 г. совпадает по обеим моделям.
Модель рядов динамики по данным ГУП «Каспий» за исключением 2012 г. имеет следующий вид:
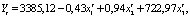
(R2 =0,73), (4)
где Yt – это выручка от реализации винограда, 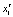 – затраты на производство в растениеводстве,
– затраты на производство в растениеводстве, 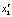 – затраты на уход за молодыми виноградниками,
– затраты на уход за молодыми виноградниками,  – урожайность винограда.
– урожайность винограда.
В первом варианте (модель (1)) 99 % вариации результативного показателя обусловлена вариацией выбранных показателей-факторов, во втором (модель (4)) – 73 %.
Оценку качества построенной модели дает средняя ошибка аппроксимации. Она рассчитывается по формуле
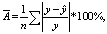
где y, 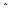 – фактические и расчетные (полученные по модели) значения результативного показателя; n – число единиц совокупности.
– фактические и расчетные (полученные по модели) значения результативного показателя; n – число единиц совокупности.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических – в первом варианте равна 2 %, а во втором – 3 %. Допустимый предел значений составляет не более 8–10 %.
Статистическую значимость моделей определим на основе F-критерия Фишера. F-mecm – оценивание качества уравнения регрессии – состоит в проверке гипотезы H0 статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
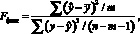
где y, 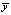 ,
, 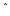 – фактические, среднее и расчетные (полученные по модели) значения результативного показателя; n – число единиц совокупности; m – число параметров при переменных x.
– фактические, среднее и расчетные (полученные по модели) значения результативного показателя; n – число единиц совокупности; m – число параметров при переменных x.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01.
Если Fтабл < Fфакт, то H0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл < Fфакт, то гипотеза H0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии [1, 5].
Для модели (1) фактическое значение критерия Фишера составило 0,9, что меньше табличного значения при α = 0,05. Для модели (4) фактическое значение критерия Фишера составило 46,4, что превышает табличное значение при α = 0,05. Во втором случае можно говорить о статистической значимости модели рядов динамики, а следовательно, надежности полученных по ней прогнозных значений.
Проверка адекватности выбранных моделей реальному процессу (в частности, адекватности полученной кривой роста) строится на анализе остаточной компоненты.
Если вид функции выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т.к. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция остатков.
Существует несколько приемов обнаружения автокорреляции. Наиболее распространенным является подход, опирающийся на критерий Дарбина – Уотсона. Тест Дарбина – Уотсона связан с проверкой гипотезы об отсутствии автокорреляции первого порядка, т.е. автокорреляции между соседними остаточными членами ряда. При этом критическая статистика определяется по формуле
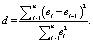
Можно показать, что величина d приближенно равна
d ≈ 2(1 – r1),
где r1 – коэффициент автокорреляции первого порядка (т.е. парный коэффициент корреляции между двумя последовательностями остатков e1, e2,…,en –1 и e2, e3,…, en).
Близость значения статистики d к нулю означает наличие высокой положительной автокорреляции (коэффициент r1 близок к единице); близость значения статистики d к четырем означает наличие высокой отрицательной автокорреляции (коэффициент r1 близок к минус единице). Естественно, в случае отсутствия автокорреляции значение статистики d будет близким к двум (коэффициент r1 не сильно отличается от нуля).
Применение на практике критерия Дарбина – Уотсона основано на сравнении расчетного значения статистики d с пороговыми, граничными значениями d1 и d2.
Граничные значения d1 и d2, зависящие от числа наблюдений n, количества объясняющих переменных в модели, уровня значимости α, находятся по таблицам (авторами критерия составлены таблицы для α = 0,05, α = 0,025 и α = 0,01).
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина – Уотсона следующий.
Выдвигается гипотеза H0 об отсутствии автокорреляции остатков. Пусть альтернативная гипотеза состоит в наличии в остатках положительной автокорреляции первого порядка.
Тогда при сравнении расчетного значения статистики d с d1 и d2 возможны следующие варианты.
1. Если d < d1, то гипотеза H0 об отсутствии автокорреляции отвергается (с вероятностью ошибки, равной α) в пользу гипотезы о положительной автокорреляции.
2. Если d > d2, то гипотеза H0 не отвергается.
3. Если d1 ≤ d ≤ d2, то нельзя сделать определенный вывод по имеющимся исходным данным (значение d попало в область неопределенности).
Если альтернативной является гипотеза о наличии в остатках отрицательной автокорреляции первого порядка, то с пороговыми, граничными значениями d1 и d2 сравнивается величина 4 – d (при d > 2).
При этом возможны следующие варианты.
1. Если 4 – d > d1, то гипотеза H0 об отсутствии автокорреляции отвергается (с вероятностью ошибки, равной α) в пользу гипотезы об отрицательной автокорреляции.
2. Если 4 – d > d2, то гипотеза H0 не отвергается.
3. Если d1 ≤ 4 – d > d2, то нельзя сделать определенный вывод по имеющимся исходным данным [4].
Для модели рядов динамики, построенной по данным ГУП «Каспий» без учета данных за 2012 г. (модель (4)), расчетное значение критерия Дарбина – Уотсона равно 2,16. Границы интервала (d1 и d2) критических значений критерия Дарбина – Уотсона при уровне значимости α = 0,05 равны 0,37 и 2,29 соответственно. Тогда гипотеза H0 не отвергается.
Для модели рядов динамики, построенной по данным ГУП «Каякентский» (модель (3)), расчетное значение критерия Дарбина – Уотсона равен 2,17. Границы интервала (d1 и d2) критических значений критерия Дарбина – Уотсона при уровне значимости α = 0,05 равны 0,46 и 2,13 соответственно. Тогда гипотеза H0 не отвергается.
Для модели рядов динамики, построенной по данным ГУП «Кировский» (модель (2)), расчетное значение критерия Дарбина – Уотсона равно 2,15. Границы интервала (d1 и d2) критических значений критерия Дарбина – Уотсона при уровне значимости α = 0,05 равны 0,46 и 2,13 соответственно. Тогда гипотеза H0 об отсутствии автокорреляции не отвергается.
Таким образом, сельское хозяйство – отрасль, играющая особую роль в экономике РД, на ее долю приходится более одной трети валового регионального продукта республики. Ключевым показателем развития сельского хозяйства является валовая продукция, производимая в этой отрасли.
Возрастание роли прогнозирования в АПК обусловлено ускорением научно-технического прогресса, развивающейся интеграцией комплекса с другими отраслями экономики, усилением неопределенности, влиянием множества факторов на развитие сфер АПК и др.
Применение экономико-математических методов в прогнозировании позволяет существенно снизить степень неопределенности. Для этого разработаны модели временных рядов и рядов динамики, позволяющие выявить и оценить сложившиеся динамические тенденции изменения показателей предприятий аграрной сферы, комплексное использование которых позволяет обеспечить обоснованные краткосрочные и среднесрочные прогнозы.
Библиографическая ссылка
Касимова Т.М., Гаджикурбанов З.Н. ПРОГНОЗИРОВАНИЕ ПОКАЗАТЕЛЕЙ ПРОИЗВОДСТВА ВИНОГРАДА С ПОМОЩЬЮ МОДЕЛЕЙ РЯДОВ ДИНАМИКИ // Фундаментальные исследования. – 2017. – № 4-1. – С. 146-150;URL: https://fundamental-research.ru/ru/article/view?id=41451 (дата обращения: 24.04.2024).



