Объединяя основные авторские подходы к определению содержания экономической категории «инновационный потенциал», можно выделить следующие:
– мера способности и готовности экономической системы к внедрению инноваций;
– ресурсный – совокупность ресурсов экономической системы для осуществления инновационной деятельности. То есть комплекс ресурсов, в числе которых выделяют кадры, финансы, материально-техническую базу и др. В некоторых работах – сумма названных потенциалов;
– совокупность не ресурсов, а возможностей экономической системы использовать эти ресурсы. Этот подход тесно связан с предыдущим [1, 2].
Ресурсный потенциал региона – это совокупность различных видов ресурсов, которыми располагает в определенный момент регион и возможности которых могут быть использованы для достижения стратегических целей регионального развития [3, 4].
При оценке ресурсного потенциала наиболее важными являются следующие его составляющие: производственный потенциал, трудовой потенциал, образовательный потенциал, научно-технический потенциал и т.д.
Целью настоящего исследования является разработка математической и компьютерной моделей для оценки инновационного потенциала регионов.
В первой части исследования осуществляется выявление динамических тенденций изменения показателей ресурсного потенциала регионов ЮФО и СКФО в 2005, 2010 и 2016 гг. с помощью методов эконометрического моделирования. Для этого необходимо разработать математическую модель, перевести ее на компьютерную основу, и на ее основе провести оценку полученных результатов.
Для этой цели рассчитаны основные статистические характеристики (коэффициент детерминации, F-критерия Фишера и др.), позволяющие оценивать качество построенных уравнений регрессии и статистическую значимость параметров уравнений.
Связи и зависимости в экономике можно изучить разными методами. Наиболее эффективным методом является выявление и оценка связей и зависимостей с помощью эконометрических уравнений.
Пространственными данными называется совокупность информации, которая характеризует различные объекты, однако полученная за один и тот же период или момент времени [5].
Пространственные данные являются выборочной совокупностью из некоторой генеральной совокупности. В настоящем исследовании в качестве таких данных выбраны данные регионов ЮФО и СКФО РФ за 2005, 2010 и 2016 гг.
Математически уравнение регрессии имеет вид
Y = f(x1, x2, … , xp),
Y – величина результативного показателя (зависимой переменной),
x1, x2, … , xp – величины 1-го, 2-го, ..., p-го показателей-факторов (независимых переменных) [5, 6].
В качестве результативного показателя выбран y – валовый региональный продукт (тыс. руб.), а показателей-факторов x1 – среднегодовая численность занятых в экономике (тыс. чел.), x2 – стоимость основных производственных фондов (тыс. руб.), x3 – выпуск специалистов с высшим образованием (тыс. чел.), x4 – общие затраты на технологические инновации (тыс. руб.).
Нами построены зависимости линейного, степенного видов. Коэффициенты этих зависимостей имеют экономическое истолкование.
В табл. 1–4 a, b – параметры уравнения; ta, tb – t-критерии Стьюдента; Sey – стандартная ошибка y; r2 – коэффициент детерминации; F – критерий Фишера; df – число степеней свободы. Согласно табл. 1 модели линейного и степенного видов в 2005, 2010 и 2016 гг. соответственно имеют вид
 , (1)
, (1)
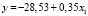 , (2)
, (2)
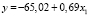 , (3)
, (3)
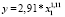 , (4)
, (4)
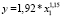 , (5)
, (5)
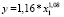 . (6)
. (6)
В линейных уравнениях коэффициент перед x показывает предельную эффективность показателя-фактора. В моделях (1–3) при увеличении численности занятых в экономике на 1 тыс. чел. ВРП увеличивается на 0,14 млрд руб. (140 млн руб.) в 2005 г.; в 2010 г. – на 0,35 млрд руб. (350 млн руб.); в 2016 г. – на 0,69 млрд руб. (690 млн руб.), т.е. в каждую пятилетку этот показатель увеличивается в 2 раза.
Таблица 1
Параметры и статистические характеристики зависимости ВРП от среднегодовой численности занятых в экономике, полученные по данным регионов СКФО и ЮФО за 2005, 2010 и 2016 гг.
|
a |
b |
ta |
tb |
Sey |
r2 |
F |
df |
||
|
2005 |
линейн |
–10,58 |
0,14 |
0,7 |
18,75 |
17,74 |
0,97 |
351,71 |
10 |
|
степ |
2,91 |
1,11 |
0,08 |
30,64 |
0,14 |
0,99 |
938,96 |
10 |
|
|
2010 |
линейн |
–28,53 |
0,35 |
17,2 |
20,04 |
43,21 |
0,98 |
401,42 |
10 |
|
степ |
1,92 |
1,15 |
0,23 |
29,19 |
0,14 |
0,98 |
852,14 |
10 |
|
|
2016 |
линейн |
–65,02 |
0,69 |
49,94 |
13,81 |
124,46 |
0,95 |
190,6 |
10 |
|
степ |
1,16 |
1,08 |
0,38 |
17,52 |
0,23 |
0,97 |
306,94 |
10 |
Коэффициент при x1 в моделях степенного вида является коэффициентом эластичности. Согласно уравнениям (4)–(6) увеличение среднегодовой численности занятых в экономике на 1 % приводит к увеличению ВРП на 1,1 % как в 2005, так и в 2010, 2016 гг. То есть отзывчивость результативного признака на изменение трудового потенциала слабая.
Параметр b статистически значим во всех моделях, параметр a – в линейной зависимости в 2010 и 2016 гг. Индексы детерминации в табл. 1 высокие и показывают, что вариация ВРП в СКФО и ЮФО в рассматриваемые годы на 95–99 % зависит от изменения среднегодовой численности занятых в экономике. Критические значения F-критерия Фишера превышают табличное значение, которое равно 241,8. Это свидетельствует о статистической значимости построенных уравнений.
Построим уравнения зависимости ВРП от стоимости основных фондов по тем же показателям. Результаты представлены в табл. 2.
Согласно табл. 2 модели линейного и степенного видов в 2005, 2010 и 2016 гг. соответственно имеют вид
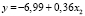 , (7)
, (7)
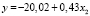 , (8)
, (8)
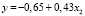 , (9)
, (9)
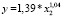 , (10)
, (10)
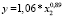 , (11)
, (11)
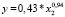 . (12)
. (12)
Согласно моделям (7)–(9) при увеличении стоимости основных фондов на 1 млн руб. ВРП увеличивается на 360 млн руб. в 2005 г.; в 2010 и в 2016 гг. – на 0,43 млрд руб. (430 млн руб.).
Согласно рассчитанным значениям t-критерия Стьюдента параметр b статистически значим во всех моделях, параметр a – в линейной зависимости в 2010 и 2016 гг. Индексы детерминации высокие и показывают, что вариация ВРП в СКФО и ЮФО в рассматриваемые годы на 96–99 % зависит от стоимости основных фондов. Критические значения F-критерия Фишера превышают табличное значение, что свидетельствует о статистической значимости построенных уравнений.
В уравнениях (10)–(12) при увеличении стоимости основных фондов на 1 % ВРП увеличивается на 1,1 % в 2005, 0,01 в 2010, 0,94 в 2016 гг. То есть отзывчивость результативного признака на изменение производственного потенциала слабая.
Построим уравнения зависимости ВРП от выпуска специалистов с высшим образованием. Результаты приведены в табл. 3.
Таблица 2
Параметры и статистические характеристики зависимости ВРП от стоимости основных фондов, полученные по данным регионов СКФО и ЮФО за 2005, 2010 и 2016 гг.
|
a |
b |
ta |
tb |
Sey |
r2 |
F |
df |
||
|
2005 |
линейн |
–6,99 |
0,36 |
3,01 |
45,68 |
7,37 |
0,99 |
2086,40 |
10 |
|
степ |
1,39 |
1,04 |
0,20 |
27,31 |
0,16 |
0,99 |
745,59 |
10 |
|
|
2010 |
линейн |
–20,02 |
0,43 |
17,69 |
19,14 |
45,17 |
0,97 |
366,44 |
10 |
|
степ |
1,06 |
0,89 |
0,39 |
14,80 |
0,28 |
0,96 |
219,04 |
10 |
|
|
2016 |
линейн |
–0,65 |
0,43 |
19,45 |
33,65 |
52,15 |
0,99 |
1132,29 |
10 |
|
степ |
0,43 |
0,94 |
0,37 |
15,80 |
0,25 |
0,96 |
249,68 |
10 |
Таблица 3
Параметры и статистические характеристики зависимости ВРП от выпуска специалистов с высшим образованием, полученные по данным регионов СКФО и ЮФО за 2005, 2010 и 2016 гг.
|
a |
b |
ta |
tb |
Sey |
r2 |
F |
df |
||
|
2005 |
линейн |
–20,86 |
16,04 |
17,46 |
8,23 |
38,25 |
0,87 |
67,81 |
10 |
|
степ |
1,74 |
1,33 |
0,17 |
14,43 |
0,29 |
0,95 |
208,18 |
10 |
|
|
2010 |
линейн |
–72,86 |
42,47 |
46,55 |
7,88 |
103,23 |
0,86 |
62,08 |
10 |
|
степ |
2,34 |
1,45 |
0,28 |
9,05 |
0,44 |
0,89 |
81,87 |
10 |
|
|
2016 |
линейн |
–66,04 |
130,58 |
118,86 |
5,48 |
278,52 |
0,75 |
30,05 |
10 |
|
степ |
4,04 |
1,35 |
0,20 |
8,35 |
0,46 |
0,87 |
69,71 |
10 |
 , (13)
, (13)
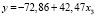 , (14)
, (14)
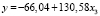 , (15)
, (15)
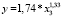 , (16)
, (16)
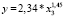 , (17)
, (17)
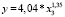 . (18)
. (18)
Согласно моделям (13)–(18) параметры a и b статистически значимы во всех случаях. Индекс детерминации высокий, это говорит о сильной связи между показателями. Критические значения F-критерия Фишера превышают табличное значение, что свидетельствует о статистической значимости построенных уравнений.
В уравнениях (16)–(18) увеличение выпуска специалистов с высшим образованием на 1 % приводит к увеличению ВРП на 1,3 % как в 2005, так и в 2010, 2016 гг. То есть отзывчивость результативного признака на изменение образовательного потенциала слабая. Это может быть связано с тем, что воздействие выбранного фактора на результативный показатель запаздывает во времени. В таких ситуациях целесообразнее строить модели с распределенным лагом.
В табл. 4 представлены результаты построения зависимости ВРП от общих затрат на технологические инновации.
Согласно табл. 4 модели линейного и степенного видов в 2005, 2010 и 2016 гг. соответственно имеют вид
 , (19)
, (19)
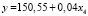 , (20)
, (20)
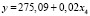 , (21)
, (21)
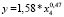 , (22)
, (22)
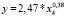 , (23)
, (23)
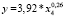 . (24)
. (24)
Рассматривая зависимость ВРП от показателя научно-технического потенциала получены следующие результаты: при увеличении затрат на технологические инновации на 1 % ВРП увеличивается на 0,5; 0,4 и 0,3 % соответственно в 2005, 2010 и 2016 гг.
Согласно табл. 4 в моделях (19)–(24) параметры a и b статистически значимы. Согласно значениям индекса детерминации для модели (21) вариация результативного показателя лишь на 30 % объясняется выбранным показателем-фактором, для остальных моделей его значение колеблется в диапазоне 50–70 %. Критические значения F-критерия Фишера превышают табличное значение, что свидетельствует о статистической значимости построенных уравнений.
Таким образом, разработанные модели (1)–(24) позволяют оценивать зависимость ВРП от различных видов ресурсного потенциала в 2005, 2010, 2016 гг.
Вторая часть исследования посвящена разработке математической и компьютерной моделей на прямые расчеты для анализа инновационного потенциала регионов. Для этого введем следующие обозначения исходных данных:
ЧП – численность персонала, занятого научными исследованиями и разработками; ЧЗ – численность занятых в экономике; ЧД – численность докторов, кандидатов, докторантов, аспирантов; РВЧЗ – доля работников с высшим образованием в численности занятых в экономике; ЧС – численность студентов; ИОФ – степень износа основных фондов; ООФ – коэффициент обновления основных фондов; ОФ – стоимость основных фондов; ИОК – инвестиции в основной капитал; ВРП – валовый региональный продукт; ЗН – внутренние затраты на научные исследования и разработки; ОИИ – доля организаций, использовавших интернет, в общем числе организаций, использовавших ИКТ; ЗИКТ – затраты на ИКТ; ЧПК – число ПК на 100 работников; ЧА – доля числа абонентов сотовой связи в численности населения.
Таблица 4
Параметры и статистические характеристики зависимости ВРП от общих затрат на технологические инновации, полученные по данным регионов СКФО и ЮФО за 2005, 2010 и 2016 гг.
|
a |
b |
ta |
tb |
Sey |
r2 |
F |
df |
||
|
2005 |
линейн |
59,73 |
0,03 |
29,96 |
2,04 |
89,68 |
0,61 |
4,15 |
10 |
|
степ |
1,58 |
0,47 |
0,47 |
5,29 |
0,71 |
0,74 |
27,95 |
10 |
|
|
2010 |
линейн |
150,55 |
0,04 |
94,15 |
1,05 |
263,07 |
0,45 |
1,10 |
10 |
|
степ |
2,47 |
0,38 |
0,78 |
2,94 |
0,97 |
0,46 |
8,65 |
10 |
|
|
2016 |
линейн |
275,09 |
0,02 |
161,19 |
1,76 |
487,05 |
0,34 |
3,10 |
10 |
|
степ |
3,92 |
0,26 |
0,47 |
3,56 |
0,86 |
0,56 |
12,71 |
10 |
Обозначим также систему показателей оценки инновационного потенциала региона.
Показатели научного потенциала:
Н1 – коэффициент, который показывает долю численности персонала, занятого исследованиями и разработками, в численности занятых в экономике;
Н2 – коэффициент, который показывает отношение численности докторов, кандидатов, докторантов, аспирантов к численности занятых в экономике.
Показатели кадрового потенциала:
К1 – коэффициент, показывающий долю работников с высшим образованием в численности занятых в экономике;
К2 – коэффициент, показывающий отношение численности студентов вузов к численности занятых в экономике.
Показатели технического потенциала:
Т1 – коэффициент годности основных фондов;
Т2 – коэффициент обновления основных фондов;
Т3 – фондовооруженность труда.
Показатели информационно-коммуникационной составляющей (ИКС):
И1 – коэффициент, показывающий долю организаций, использовавших интернет, в общем числе организаций, использовавших ИКТ;
И2 – коэффициент, который показывает отношение затрат на ИКТ к ВРП;
И3 – число персональных компьютеров на 100 работников;
И4 – коэффициент, показывающий долю числа абонентов сотовой связи в численности населения.
Показатели финансово-экономического потенциала:
Э1 – коэффициент, показывающий отношение объемов инвестиций в основной капитал к ВРП;
Э2 – коэффициент, показывающий отношение внутренних затрат на исследования и разработки к ВРП.
Математическая модель для анализа инновационного потенциала региона имеет следующий вид:
|
Н1 = ЧП/ЧЗ; |
Э1 = ИОК/ВРП; |
|
Н2 = ЧД/ЧЗ; |
Э2 = ЗН/ВРП; |
|
К1 = РВЧЗ/100; |
И1 = ОИИ/100; |
|
К2 = ЧС/ЧЗ; |
И2 = ЗИКТ/ВРП; |
|
Т1 = 1-(ИОФ/100); |
И3 = ЧПК/100; |
|
Т2 = ООФ/100; |
И4 = ЧА. |
|
Т3 = ОФ/ЧЗ; |
По этой модели рассчитаны показатели инновационного потенциала регионов Северо-Кавказского федерального округа. Результаты представлены в табл. 5.
Согласно табл. 5 в регионах СКФО в 2016 г. наблюдается низкая эффективность использования научного потенциала. Фондовооруженность труда – показатель технического потенциала – свидетельствует об эффективности использования производственных фондов во всех регионах.
Построенная компьютерная модель позволяет рассчитывать показатели инновационного потенциала в различные периоды. Например, наглядно сравнить показатели инновационного потенциала РД позволяет диаграмма на рисунке.
Таблица 5
Показатели инновационного потенциала регионов СКФО по данным за 2016 г.
|
Республика Дагестан |
Республика Ингушетия |
Кабардино-Балкарская Республика |
Карачаево-Черкесская Республика |
Республика Северная Осетия – Алания |
Чеченская Республика |
Ставропольский край |
|
|
Н1 |
0,002 |
0,002 |
0,003 |
0,003 |
0,002 |
0,001 |
0,002 |
|
Н2 |
0,001 |
0,001 |
0,002 |
0,002 |
0,003 |
0,001 |
0,002 |
|
К1 |
0,290 |
0,253 |
0,300 |
0,358 |
0,422 |
0,194 |
0,341 |
|
К2 |
0,085 |
0,116 |
0,068 |
0,077 |
0,100 |
0,089 |
0,079 |
|
Т1 |
0,564 |
0,515 |
0,603 |
0,553 |
0,485 |
0,506 |
0,524 |
|
Т2 |
0,138 |
0,138 |
0,081 |
0,138 |
0,023 |
0,138 |
0,101 |
|
Т3 |
1,199 |
0,943 |
0,733 |
0,982 |
0,691 |
1,132 |
1,056 |
|
Э1 |
0,429 |
0,034 |
0,265 |
0,221 |
0,206 |
0,435 |
0,231 |
|
Э2 |
0,002 |
0,001 |
0,005 |
0,006 |
0,004 |
0,002 |
0,002 |
|
И1 |
0,988 |
0,899 |
0,789 |
0,862 |
0,834 |
0,973 |
0,935 |
|
И2 |
0,003 |
0,064 |
0,004 |
0,008 |
0,006 |
0,003 |
0,008 |
|
И3 |
0,340 |
0,450 |
0,400 |
0,390 |
0,360 |
0,400 |
0,430 |
|
И4 |
1,231 |
1,284 |
1,445 |
1,339 |
1,486 |
1,337 |
1,583 |
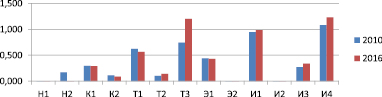
Показатели инновационного потенциала РД по данным за 2010 и 2016 гг.
Таким образом, разработанные в рамках настоящего исследования математические и компьютерные модели являются эффективным инструментом анализа инновационного потенциала регионов.
Библиографическая ссылка
Касимова Т.М. ОЦЕНКА ИННОВАЦИОННОГО ПОТЕНЦИАЛА РЕГИОНОВ МЕТОДАМИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ // Фундаментальные исследования. – 2018. – № 3. – С. 40-45;URL: https://fundamental-research.ru/ru/article/view?id=42100 (дата обращения: 20.04.2024).



