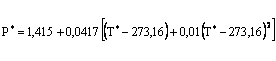 (1)
(1)
Образование гидратов в пористой среде при наличии центров кристаллизации имеет объемно-диффузионный характер. Одним из основных факторов, определяющих условия существования плотных гидратов в пористой среде, является упругость газа в водном растворе, находящемся в контакте с гидратом rw и в гидрате rH при заданной температуре. Величина rH определяется составом гидрата и его температурой. Параметр rw зависит от растворимости газа в воде при заданных давлении и температуре [2].
Условием существования гидрата является rw ³ rH. Растворимость газа в воде, находящейся в контакте с гидратом, всегда ниже, чем в отсутствии гидрата [2].
Степень газонасыщенности водного раствора, контактирующего с гидратом, определяется диффузионными потоками газа:
- потоком рассеяния в вышележащих горизонтах или в омывающие воды (Д1);
- потоком из нижележащих пластов (Д2).
Гидрат не будет диссоциировать при Д2 ³ Д1. Из этого условия следует, что чем глубже гидросодержащие породы, чем меньше и однороднее поры, тем ниже Д1, а следовательно, тем выше возможность сохранения гидрата.
При изменении горнотехнических условий происходит понижение давления газа ниже давления разложения гидрата при существующей пластовой температуре, т.е. rw становится меньше rH (rw < rH), что вызывает диссоциацию гидратной фазы, т.е. газ переходит в свободное состояние и существенно изменяет газодинамику угленосной среды.
Для построения математической модели фазовых переходов метана выделим элементарный объем горного массива V, ограниченный поверхностью G. Будем предполагать, что в этом объеме газ находится в трехфазном состоянии (свободном, сорбированном и гидратном). Тогда масса газа, заключенного в этом объеме, в момент времени t будет равен
![]() (2)
(2)
где ri - плотность газа в каждой фазе, r(x1,x2,x3) - радиус-вектор элемента объема dV.
В процессе движения из объема V через его границу G в единицу времени вытекает количество свободного газа, равное
![]() (3)
(3)
где r1 - плотность свободного газа,
n - единичный вектор внешней нормали к поверхности G.
Тогда баланс газа за время dt будет
![]() (4)
(4)
Для течений, не имеющих сильных разрывов, интегральные уравнения заменим дифференциальными, описывающими процесс фазового перехода метана. Понижение давления до величины разложения гидрата определило подвижную границу диссоциации газа ![]() .
.
В зоне I (0 ≤ x ≤![]() ) произошла десорбция газа и закончилось разложение гидрата и газ перешел в свободное состояние. В зоне II (
) произошла десорбция газа и закончилось разложение гидрата и газ перешел в свободное состояние. В зоне II ( ![]() ≤ x < ∞) процесс диссоциации еще не наступил и гидратная фаза сохраняется.
≤ x < ∞) процесс диссоциации еще не наступил и гидратная фаза сохраняется.
В одномерном случае процесс диссоциации описывается следующей краевой задачей:
t < t1,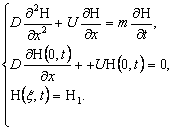 (5)
(5)
t ³ t1, x <![]() ,
, 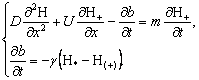 (6)
(6)
 (7)
(7)
Здесь
= rRT соответственно в зонах диссоциации и гидратирования,
D = lU - коэффициент конвективной диффузии, м2/сутки;
l - параметр дисперсии, M;
g = hU - коэффициент гидратирования (диссоциации), сутки-1;
h - константа скорости гидратирования, м-1;
t1 - время окончания первой стадии, сутки.
Введем безразмерные координаты
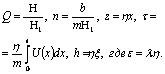 (8)
(8)
1. Рассмотрим стадию диссоциации газа в зоне ![]() . Задача (5) в обозначениях (8) принимает вид
. Задача (5) в обозначениях (8) принимает вид
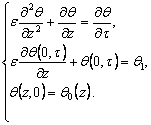 (9)
(9)
Решение задачи (9) в виде составного разложения по степеням e имеет вид [3]
![]() (10)
(10)
Подставляя (10) в (9) и приравнивая члены при одинаковых степенях e,получим
![]() (11)
(11)
![]() (12)
(12)
 (13)
(13)
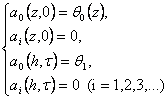 (14)
(14)
Решая (11)-(14) методом характеристик, найдем
 (15)
(15)
Если ![]() , то
, то ![]() При
При ![]() функция
функция ![]() определяется из (12), (13) при конкретном задании функции
определяется из (12), (13) при конкретном задании функции ![]() .
.
Так как θ1 > θ0(h), то на характеристике ![]() функция
функция ![]() терпит разрыв, т.е. разложение решения задачи (11) в виде (12) справедливо всюду, за исключением окрестности характеристики
терпит разрыв, т.е. разложение решения задачи (11) в виде (12) справедливо всюду, за исключением окрестности характеристики ![]() . В работе [3] приведено решение данной задачи в виде
. В работе [3] приведено решение данной задачи в виде
 (16)
(16)
Общее решение, справедливое во всей области фазовых превращений метана, можно получить методом аддитивного составления [3]
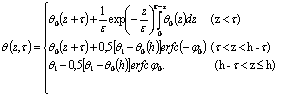 (17)
(17)
Формула (17) справедлива при ![]()
При ![]() и
и ![]() из (17) имеем
из (17) имеем
![]() (18)
(18)
При этих условиях точное решение задачи (11) получено в виде
 (19)
(19)
Незначительное различие точного (19) и приближенного решения (18) указывает на эффективность приближенных методов для решения данной задачи.
Из анализа полученного решения можно определить подвижную границу диссоциации газа ![]() . Граница
. Граница ![]() движется противоположно направлению фильтрации. При большой скорости ведения горных работ граница
движется противоположно направлению фильтрации. При большой скорости ведения горных работ граница ![]() может приближаться к кромке пласта. Для приблизительной оценки величины
может приближаться к кромке пласта. Для приблизительной оценки величины ![]() предположим, что давление на границе зоны диссоциации совпадает с давлением свободного газа в начальный период разложения гидрата, т.е.
предположим, что давление на границе зоны диссоциации совпадает с давлением свободного газа в начальный период разложения гидрата, т.е. ![]() , тогда уравнение баланса газа на границе
, тогда уравнение баланса газа на границе ![]() можно представить в виде
можно представить в виде
![]() (20)
(20)
где ![]() определяется по формуле (1). Разделяя переменные в уравнении (20), найдем
определяется по формуле (1). Разделяя переменные в уравнении (20), найдем
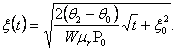 (21)
(21)
Из формулы (21) следует, что гидратное давление ![]() снижается довольно резко до некоторого значения, соответствующего разложению гидрата, что свидетельствует о быстром его разложении и незначительных размерах зоны диссоциации
снижается довольно резко до некоторого значения, соответствующего разложению гидрата, что свидетельствует о быстром его разложении и незначительных размерах зоны диссоциации
( ![]() ).
).
Расчеты по формуле (21) показывают, что зона диссоциации находится в зоне упругих деформаций угольного пласта. Этот факт говорит о том, что в этой области происходит начительный рост концентрации газа. Общее количество диссоциированного газа будет
![]() (22)
(22)
Исходя из формулы состава кристаллогидрата (![]() ) и с учетом выражения (22) можно определить массу газа и число объемов газа в одном объеме гидрата. Например, для
) и с учетом выражения (22) можно определить массу газа и число объемов газа в одном объеме гидрата. Например, для ![]() МПа, t=0 оС. Число объемов газа в единице объема гидрата составляет 101,44 кг/м3. Таким образом, один объем гидрата содержит более сотни объемов газа, это свидетельствует о том, что гидраты (особенно метана) отличаются значительными запасами внутренней энергии и высокой концентрацией газа. Следовательно, зоны разложения гидрата являются зонами повышенной газодинамической активности пласта.
МПа, t=0 оС. Число объемов газа в единице объема гидрата составляет 101,44 кг/м3. Таким образом, один объем гидрата содержит более сотни объемов газа, это свидетельствует о том, что гидраты (особенно метана) отличаются значительными запасами внутренней энергии и высокой концентрацией газа. Следовательно, зоны разложения гидрата являются зонами повышенной газодинамической активности пласта.
Список литературы
- Веригин Н.Н. О разложении гидрата газа в плате. //МЖГ.- 1982 - №4.-с.171 -173.
- Макогон Ю.Ф. Гидраты природных газов.- М.: Недра,1974.
- Ван-Дайк М. Методы возмущений в механике жидкости. М., Мир, 1967.
Библиографическая ссылка
Беспятов Г.А. ФАЗОВЫЕ ПЕРЕХОДЫ МЕТАНА ПРИ ИЗМЕНЕНИИ ТЕРМО-ДИНАМИЧЕСКИХ ПАРАМЕТРОВ ГОРНОГО МАССИВА // Фундаментальные исследования. – 2004. – № 5. – С. 91-94;URL: https://fundamental-research.ru/ru/article/view?id=5809 (дата обращения: 25.04.2024).



