Процессы переноса на фрактальных (самоподобных) объектах называются странными или аномальными. Среднеквадратичное удаление блуждающей частицы ![]() описывается так [1]:
описывается так [1]:
![]() , (1)
, (1)
где D - обобщенный коэффициент переноса, t - время, μ - показатель.
В узком смысле слова термин «странный перенос» предполагает нелинейную (μ ≠ 1) зависимость ![]() от t. Величина μ варьируется следующим образом [1]:
от t. Величина μ варьируется следующим образом [1]:
![]() . (2)
. (2)
При 0≤μ<1 говорят о субдиффузионных процессах переноса, при 1<μ≤2 - о супердиффузионных процессах. Также было введено понятие о супербаллистическом процессе, соответствующем условию μ>2. Показатель μ связан с показателем Херста Н так [1]:
![]() . (3)
. (3)
В свою очередь, величина Н зависит от структуры полимера, характеризуемой ее фрактальной размерностью df [2]:
![]() . (4)
. (4)
И наконец, размерность траектории блуждания частицы-диффузанта dw определяется следующим образом [1]:
![]() . (5)
. (5)
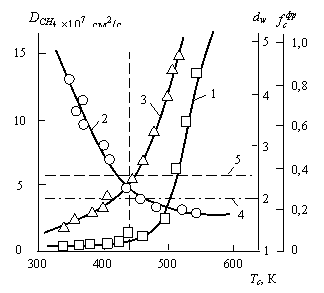
Рисунок 1. Зависимости ![]() (1), dw (2) и
(1), dw (2) и ![]() (3) от Тс. 4 - размерность броуновского движения, 5 - порог перколяции по схеме перекрывающихся сфер.
(3) от Тс. 4 - размерность броуновского движения, 5 - порог перколяции по схеме перекрывающихся сфер.
Очевидно, что изменение режима переноса (диффузии) определяет большое (на порядки величины) изменение коэффициента диффузии. Поэтому важно установить взаимосвязь между структурой полимера и режимом диффузии. Для этой цели будут использованы экспериментальные зависимости коэффициента диффузии по метану ![]() от температуры стеклования Тс для 11 полимеров [3].
от температуры стеклования Тс для 11 полимеров [3].
На рис. 1 приведена зависимость ![]() (Тс) для указанных 11 полимеров. Как можно видеть, при Тс>440 К наблюдается резкий рост
(Тс) для указанных 11 полимеров. Как можно видеть, при Тс>440 К наблюдается резкий рост ![]() по мере увеличения Тс в довольно узком интервале температур (440-540 К). Кроме того, при Тс ≈ 440 К величина dw достигает значения случайного броуновского движения (dw=2) и при дальнейшем росте Тс dw< 2, т.е., происходит переход к баллистическим траекториям.
по мере увеличения Тс в довольно узком интервале температур (440-540 К). Кроме того, при Тс ≈ 440 К величина dw достигает значения случайного броуновского движения (dw=2) и при дальнейшем росте Тс dw< 2, т.е., происходит переход к баллистическим траекториям.
Получить объяснение этим изменениям процесса переноса можно в рамках фрактальной теории свободного объема [4]. Как показано ранее [4, 5], представление микрополостей флуктуационного свободного объема, через которые реализуется диффузия в полимерах, в виде трехмерной сферы является упрощенным и более точно рассматривать эту микрополость как Df-мерную сферу (Df - размерность областей локализации избыточной энергии, равная 1+(3-df)-1). В такой трактовке объем микрополости ![]() дается следующим образом [5]:
дается следующим образом [5]:
![]() , (6)
, (6)
где rh - радиус микрополости свободного объема.
Если обозначить объем микрополости в трехмерном представлении как Vh, относительный фрактальный свободный объем ![]() можно рассчитать так [5]:
можно рассчитать так [5]:
![]() , (7)
, (7)
где относительную долю флуктуационного свободного объема fc можно принять равной 0,060 для твердофазных полимеров [5].
Зависимость рассчитанной таким образом величины ![]() от Тс показана на рис. 1 (кривая 3). Как и следовало ожидать, наблюдается увеличение
от Тс показана на рис. 1 (кривая 3). Как и следовало ожидать, наблюдается увеличение ![]() по мере роста Тс и при Тс≈440 К величина достигает порога перколяции в предположении схемы перекрывающихся сфер (микрополостей), равного 0,34±0,01 [4]. Иначе говоря, согласно теории перколяции при Тс≈440 К в полимерной мембране формируется каркас соединенных между собой микрополостей свободного объема, что облегчает условия диффузии молекул газа-диффузанта, определяет критерий dw<1 и резко повышает коэффициент диффузии
по мере роста Тс и при Тс≈440 К величина достигает порога перколяции в предположении схемы перекрывающихся сфер (микрополостей), равного 0,34±0,01 [4]. Иначе говоря, согласно теории перколяции при Тс≈440 К в полимерной мембране формируется каркас соединенных между собой микрополостей свободного объема, что облегчает условия диффузии молекул газа-диффузанта, определяет критерий dw<1 и резко повышает коэффициент диффузии ![]() .
.
Необходимо дать пояснения относительно абсолютных величин ![]() , которые при расчете по уравнению (9) могут превышать 1,0, что на первый взгляд представляется физическим абсурдом. На самом деле это означает локальный «всплеск» величины
, которые при расчете по уравнению (9) могут превышать 1,0, что на первый взгляд представляется физическим абсурдом. На самом деле это означает локальный «всплеск» величины ![]() в пределах флуктуаций усредненной величины fс, когда
в пределах флуктуаций усредненной величины fс, когда ![]() >16,7Vh. С учетом большого общего количества микрополостей (~1028 м-3) такой «всплеск» для ограниченного их числа оставляет величину fс практически неизменной, но может сильно влиять на локальные свойства полимера на молекулярном уровне.
>16,7Vh. С учетом большого общего количества микрополостей (~1028 м-3) такой «всплеск» для ограниченного их числа оставляет величину fс практически неизменной, но может сильно влиять на локальные свойства полимера на молекулярном уровне.
Таким образом, изложенные выше результаты предполагают, что переход от субдиффузионного режима к супердиффузионному обусловлен структурным фактором - образованием непрерывного перколяционного каркаса микрополостей. При этом на микроскопическом уровне процесс выглядит скорее как баллистический, чем диффузионный (μ>1, Н>0,5 и dw<2) [1]. Для супербаллистического процесса (μ>2, Н>1) согласно (4) получим df<2. Из уравнения, связывающего df и коэффициент Пуассона n
df =(1 + ν ) (8)
определим, что в этом случае ν<0. Как известно, отрицательные значения n типичны для пористых твердых тел. Следовательно, супербаллистический перенос может быть реализован только в пористых полимерных мембранах.
СПИСОК ЛИТЕРАТУРЫ
- Зеленый Л.М., Милованов А.В. Фрактальная топология и странная кинетика: от теории перколяции к проблемам космической электродинамики. Успехи физических наук, 2004, т. 174, № 8, с. 809-852.
- Шогенов В.Х., Ахкубеков А.А., Ахкубеков Р.А. Метод дробного дифференцирования в теории броуновского движения. Известия ВУЗов. Северо-Кавказский регион, 2004, № 1, с. 46-50.
- Волков В.В., Гольданский А.В., Дургарьян С.Г., Онищук В.А., Шанторович В.П., Ямпольский Ю.П. Изучение методом аннигиляции позитронов микроструктуры полимеров и ее связь с их диффузионными свойствами. Высокомолекулярные соединения А, 1987, т. 29, № 1, с. 192-197.
- Kozlov G.V., Zaikov G.E. Structure of the Polymer Amorphous State. Utrecht-Boston, Brill Academic Publishers, 2004, 465 р.
- Козлов Г.В., Сандитов Д.С., Липатов Ю.С. Структурный анализ флуктуационного свободного обема в аморфном состоянии полимеров. В кн.: Успехи в области физико-химии полимеров. М., Химия, 2004, с. 412-474.
Библиографическая ссылка
Козлов Г.В., Долбин И.В. РЕЖИМЫ ДИФФУЗИИ И ФРАКТАЛЬНЫЙ СВОБОДНЫЙ ОБЪЕМ В ТВЕРДОФАЗНЫХ ПОЛИМЕРАХ // Фундаментальные исследования. – 2005. – № 3. – С. 43-45;URL: https://fundamental-research.ru/ru/article/view?id=5846 (дата обращения: 24.04.2024).



