Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Вожегов Д.В. 1 Долженкова М.Л. 1

---

1 ГОУ ВПО «Вятский государственный университет»

В работе даётся содержательная постановка задачи логического прогнозирования на основе дедуктивного вывода с определением фактов. Вводятся новые понятия «фазовый факт» и «базовый факт», для формального описания задачи и цели определения фактов при прогнозировании. Предлагается метод логического прогнозирования на основе дедуктивного вывода с определением фактов, позволяющий предсказывать траекторию развития ситуации, а также определять базовые факты, необходимые для развития ситуации, не прерывая процесс вывода, при минимальных затратах дополнительных вычислительных ресурсов. В зависимости от исходной задачи метод позволяет определить три множества фактов: благодаря которым возможно наступление следующих событий и переход в следующие фазы, благодаря которым стал возможен переход в текущую фазу, благодаря которым возможен переход от исходной фазы до заданной. Приводится пример работы метода с использованием исчисления высказываний. Указываются отличия и преимущества метода по сравнению с ранее разработанным методом прогнозирования развития ситуаций.

Статья в формате PDF

481 KB

логическое прогнозирование развития ситуаций

дедуктивный логический вывод заключений

определение фактов

исчисление высказываний

1. Агалаков Е.В., Страбыкин Д.А., Томчук М.Н. Метод парал. логического вывода следствий для исчисления высказываний // Программные продукты и системы. – 2012. – № 2. – С. 142–144.

2. Вагин В.Н. Дедукция и обобщение в системах принятия решений. – М.: Наука, 1988. – 383 с. – (Проблемы искусств. интеллекта.).

3. Вожегов Д.В., Страбыкин Д.А. Метод параллельного дедуктивного вывода с определением фактов // Научно-технический вестник Поволжья. – 2011. – № 1. – С. 97–99.

4. Вожегов Д.В., Страбыкин Д.А. Метод параллельного абдуктивного логического вывода с определением фактов // Научно-технический вестник Поволжья. – 2012. – № 2. – С. 141–154.

5. Страбыкин Д.А., Томчук М.Н. Логическое прогнозирование развития ситуаций на основе дедуктивного вывода // Научно-технический вестник Поволжья. – 2012. – № 2. – С. 276–282.

Основной задачей системы прогнозирования является получение точного и своевременного прогноза. Но следует учесть, чтобы человек принял результат как верный, ему важнее понять, как вычислительная машина его получила. Т.е. качество работы системы прогнозирования определяется совокупной эффективностью каждой из её подсистем [2]. Иногда приоритетнее качество работы подсистемы, формирующей информацию о процессе получения прогноза, и чем хуже она работает, тем выше недоверие человека к результатам прогноза. Возникает задача совершенствования не только методов, формирующих прогноз, но и методов, собирающих информацию о том, благодаря каким данным он был получен.

Содержательная постановка задачи

Для описания задачи логического прогнозирования ситуаций введём ряд основных понятий [5].

Событие в предметной области характеризуется множеством простейших утверждений – фактов, зафиксированных в определенный момент времени [5].

Ситуация в предметной области характеризуется совокупностью событий и отношений между ними [5].

Фаза развития (состояние) ситуации представляется подмножеством событий и отношений, описывающих ситуацию [5].

Пространство развития ситуации – это множество фаз (состояний), через которые может проходить развитие ситуации.

Траектория развития ситуации – последовательность фаз, через которые проходит развитие ситуации.

Предсказание траектории развития ситуации – определение для ситуации, находящейся в текущей фазе (состоянии), одной или нескольких фаз (состояний), в которые перейдет ситуация в последующие моменты времени.

Базовый факт – однолитеральная исходная посылка вида 1 → Х или просто Х, истинная на любой фазе прогнозирования.

Фазовый факт – однолитеральные посылки, принимаемые истинными для одной фазы.

Введённые понятия позволяют сформулировать основную задачу прогнозирования развития ситуаций как задачу предсказания траектории (траекторий) развития ситуации.

Формальное описание задачи определения фактов в ходе прогнозирования

Для упрощения описания задачи прогнозирования как задачи логического вывода с определением фактов введем ряд определений [5].

Определение 1. Формула X1&X2&…&XK → Y называется формулой логического следования, а символ «→» – знаком логического следования, который разделяет формулу на левую (антецедент) и правую (консеквент) части [5].

Определение 2. Схемой логического вывода называется ориентированный граф (рис. 1, б), вершинам которого сопоставлены формулы (номера формул) посылок, причем входящие дуги помечены переменными из левых, а исходящие – из правых частей формул, и вершины соединены между собой в соответствии с суперпозицией их формул в выводе [5].

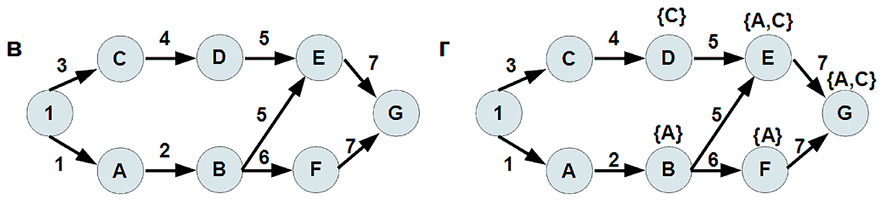
Рис. 1. Схемы: логического вывода (а), логического вывода с определением фактов (б), прогнозирования (в), прогнозирования с определением фактов (г)

Определение 3. Схемой логического вывода с определением фактов называется ориентированный граф (рис. 1, б), вершинам которого сопоставлены формулы (номера формул) посылок, а дуги помечены переменными из данных формул и базовыми фактами, благодаря которым данные переменные становятся истинными в ходе дедуктивного вывода, причем входящие дуги помечены переменными из левых, а исходящие – из правых частей формул, и вершины соединены между собой в соответствии с суперпозицией их формул в выводе; переменные свободных входящих дуг графа совпадают с переменными из левой, а свободных исходящих дуг – из правой части формулы заключения.

В качестве примера рассмотрим схему логического вывода (рис. 1) заключения A→G из множества посылок:

1) 1 → A;

2) A → B;

3) 1 → C;

4) C → D;

5) B&D → E;

6) B → F;

7) E&F → G.

Номера вершин в обеих схемах соответствуют номерам формул посылок, а соединение вершин выполнено в соответствии с суперпозицией формул в выводе (вершиной с номером 7 представлено заключение). В методе с определением фактов, кроме описанной выше информации, рядом с переменными на дугах указываются базовые факты, которые привели к их успешному выводу.

Определение 4. Схемой логического прогнозирования называется ориентированный граф (рис. 1,в), вершинам которого сопоставлены переменные из правых частей формул посылок, а дугам – номера формул посылок, вершины соединены между собой в соответствии с суперпозицией их формул в выводе.

Определение 5. Схемой логического прогнозирования с определением фактов называется ориентированный граф (рис. 1, г), вершинам которого сопоставлены переменные из правых частей формул посылок и базовые факты, благодаря которым переход в данные вершины стал возможен, а дугам – номера формул посылок, вершины соединены между собой в соответствии с суперпозицией их формул в выводе.

Формальное описание задач логического прогнозирования P может быть определено следующим образом:

P = <mC, mS, v, f, k, r>,

где mC – множество новых событий; mS – множество текущих событий и ситуаций с отношениями между ними; v∈{v+ , v– ,v0} – вид запроса: v+ – прогнозирование последующих (за заданной фазой) событий и фаз, v– – прогнозирование предшествующих (заданной фазе) событий и фаз, v0 – прогнозирование последовательностей фаз, которые сменяют друг друга при развитии ситуации от одной заданной фазы до другой; f∈{f+ , f–, f0} – множество базовых фактов: f+ – поиск базовых фактов, благодаря которым возможно наступление следующих событий и переход в следующие фазы, f– – поиск базовых фактов, благодаря которым стал возможен переход в текущую фазу, f0 – поиск базовых фактов, благодаря которым возможен переход от исходной фазы до заданной; k – конечная фаза (состояние) развития ситуации (может отсутствовать, при v = v+ , когда ставится вопрос «какая фаза (состояние) последует за текущей фазой?»); r – множество результатов прогнозирования, которое может содержать схему прогнозирования s, а также прогнозируемые в следующий момент времени фазы (состояния) m1 и последовательности фаз (состояний) mL.

Формальное описание задач логического вывода D, соответствующих задачам логического прогнозирования P, можно представить следующим образом:

D = <MH, MP, V, FH, b, d, R>,

где MH – множество новых фазовых фактов; MP – множество текущих фазовых фактов и правил; V∈{V+ , V–, V0} – вид дедуктивного логического вывода с определением фактов [3]: V+ – вывод логических следствий с определением фактов, V– – определение фазовых и базовых фактов, V0 – вывод заданного заключения с определением фактов; d – заключение (цель); FH∈{F+ , F–, F0} – множества базовых фактов, соответствующие каждому из видов вывода V; b – множество, содержащее все базовые факты, имеющиеся в исходных посылках; R – множество результатов логического вывода, которое может содержать схему вывода S и схему прогнозирования s, а также вершины схемы прогнозирования, непосредственно следующие из вершин текущего шага M1 и последовательности вершин состояний ML.

Основные виды задач логического прогнозирования и соответствующие им задачи дедуктивного вывода приведены в табл. 1.

Таблица 1

Соответствие задач прогнозирования и вывода

Метод логического прогнозирования на основе дедуктивного вывода заключений с определением фактов

Логическое прогнозирование представляет собой циклический процесс, состоящий из ряда шагов. Перед началом этого процесса задача логического прогнозирования формулируется как задача дедуктивного логического вывода с определением фактов заданного заключения: D = <MH[t], MP, V0, FH[t], b, d, R> , где MH[t] – множество фазовых фактов, поступивших на шаге t (предполагается, что MH[t] и MP образуют непротиворечивое множество). Первоначально t = 1.

В процессе прогнозирования выполняются следующие действия.

1. Принимается новое множество MH[1] фазовых фактов. Производится поиск базовых фактов FH [1], которые делают возможным переход к фазовым фактам первого шага, с помощью проверочного дедуктивного вывода b’&MP’ → MH[1]. b’ и MP’ – это подмножества множеств b и MP с одним исключенным базовым фактом. Если исключение базового факта из множеств b и MP делает вывод b’&MP’ → MH [1] невозможным, значит, этот базовый факт необходим для возникновения текущей фазы.

2. Принимается новое множество MH[t] фазовых фактов. Если какой-либо поступивший на данном шаге фазовый факт совпадает с каким-либо литералом дизъюнкта заключения d, то логический вывод считается завершенным успешно, в дальнейшем прогнозировании нет необходимости, множество базовых фактов d является множеством F = FH [t]. В этом случае выполняется пункт 10, иначе при t = 1 пункт 4, а при t > 1 следующий пункт.

3. Проверяется успешность прогноза: совпадение состояний, определяемых новым множеством фазовых фактов MH[t] и ранее прогнозированных состояний. Если прогноз успешен, то выполняется пункт 7, иначе − следующий пункт.

4. Производится решение задачи логического вывода с определением фактов MP&MH[t] ⇒ d с поиском всех нитей вывода. Если логический вывод завершается неудачно, то прогнозирование с помощью дедуктивного вывода с определением фактов невозможно. В этом случае выполняется пункт 10, иначе − следующий пункт.

5. Строится схема успешного логического вывода с определением фактов S.

6. Строится схема логического прогнозирования с определением фактов s на основе схемы логического вывода S.

7. По схеме s для множества фактов MH[t] определяются прогнозируемые вершины (состояния – ситуации), которые ожидаются на следующем шаге, а также базовые факты FH[t], необходимые для перехода в данные вершины.

8. По схеме s для множества фазовых фактов MH[t] формируются цепочки вывода ML[t] и множества базовых фактов FH[t] от текущего состояния (состояний) до состояния, соответствующего заключению d, которые представляют собой долгосрочные прогнозы.

9. Осуществляется переход к следующему шагу: значение шага t увеличивается на единицу и производится переход к пункту 2.

10. Конец. Прогнозирование завершается.

Пример прогнозирования с использованием исчисления высказываний

Рассмотрим прогнозирование с определением фактов на примере задачи, для представления знаний в которой используется исчисление высказываний.

Чтобы увидеть явные отличия этого метода с определением фактов от описанного в [5], сделаем словесное описание задачи с прикладной семантикой.

Представим задачу контроля домашних животных при постоянных заданных условиях. Имеется собака. У нее есть миски с водой и едой. Над мисками установлена камера. Если голова появляется и некоторое время находится над миской с едой – собака поела, если над миской с водой – пила. Если собака после еды или питья поспала в комнате, значит, прошли окислительно-восстановительные процессы. Если эти процессы прошли, и собака пришла на коврик к выходной двери, значит, её надо вывести на улицу. Если хозяин дома, то собаку выведут на улицу. Тогда A – миска с едой полна (базовый факт), B – миска с водой полна (базовый факт), С – собака ела, D – собака пила, E – собака спала, F – прошли о-в реакции, H – собака на коврике у двери, I – хозяин дома (базовый факт); G – собаку вывели на улицу.

Формальное описание задачи логического вывода с определением фактов (соответствующей задаче прогнозирования) имеет следующий вид.

D = <MH, MP, V0, FH[t], b, d, R>.

Исходное множество фактов MH[1] = {E}. Исходное множество посылок (MP):

1) 1 → A;

2) 1 → B;

3) A → C;

4) C&B → D;

5) C&D → E;

6) E → F;

7) F → H;

8) 1 → I;

9) I&H →G.

V0 – вывод заданного заключения d с определением фактов. Выводимое заключение d: 10) G. Множество решений R = {S, s, M1, ML}. Первоначально t = 1. b = {A, B, I}.

В процессе прогнозирования выполняются следующие действия.

1. Принимается новое множество MH[1] = {C, D}, производится поиск базовых фактов. Для этого выполняется проверочный вывод b’&MP → MH[1]. Т.к. вывод фазовых фактов MH[1] = {C, D} не успешен при отсутствии базовых фактов A или B в исходных посылках MP, то во множество FH[1] = {A, B} помещаются только эти два факта.

2. Принимается новое множество MH[1] = {C, D}. Поскольку поступившие на данном шаге фазовые факты не совпадают с литералом заключения d и t = 1, то выполняется пункт 4.

3. Производится решение задачи логического вывода с определением фактов MP&MH[1] ⇒ d. Логический вывод завершается успешно, выполняется следующий пункт.

4. Строится схема успешного логического вывода S.

5. Строится схема логического прогнозирования s на основе схемы логического вывода S (рис. 2а и б).

6. По схеме s для множества фактов MH[1] определяются прогнозируемые вершины (состояния – ситуации), которые ожидаются на следующем шаге, а также множество базовых фактов FH [1], необходимых для наступления следующего шага.

7. По схеме s для множества фактов MH[t] формируется цепочка вывода от текущего состояния (состояний) до состояния, соответствующего заключению d.

8. Осуществляется переход к следующему шагу: значение шага t увеличивается на единицу и производится переход к пункту 1 (все шаги представлены в табл. 1).

Рис. 2. Схемы: логического вывода с определением фактов (а),логического прогнозирования с определением фактов (б)

Таблица 2

Прогноз с определением базовых фактов

Рассмотрим результаты прогнозирования для разных видов вывода V.

Если MH[1] = {E} и V = V+ – вывод логических следствий, то результатом работы метода будет прогноз: E → F → Н → G. Если MH[1] = {E} и V = V+ – вывод логических следствий с определением фактов: Е → F → H → G, только если миски с едой и водой наполнены (наличие базовых фактов A и B) и человек находится в квартире (базовый факт I). Если MH[1] = {E} и V = V– – вывод логических следствий с определением фазовых фактов, то к E приводят фазовые факты С и В. Если MH[1] = {E} и V = V– – вывод логических следствий с определением базовых и фазовых фактов: к E приводят фазовые факты С и В, если миски с водой и едой были изначально наполнены (т.е. обязательно наличие базовых фактов A и B). Если MH[1] = {C, D}, d = G и V = V0 – вывод заданного заключения, то G может предшествовать С и D. Если MH[1] = {C, D}, d = G и V = V0 – вывод заданного заключения с определением фактов: G может предшествовать С и D, если изначально наполнены миски с едой (A) и водой (B) и хозяин был дома (I).

Выводы

Предложенный метод логического прогнозирования развития ситуаций на основе дедуктивного вывода с определением фактов позволяет предсказывать траекторию развития ситуации, а также определять базовые факты, необходимые для развития ситуации. Метод позволяет определять базовые факты, не прерывая процесс вывода при минимальных затратах дополнительных вычислительных ресурсов. Если в исходной базе отсутствуют факты, то накладные расходы на поиск фактов будут избыточны.

Метод основан на операции деления дизъюнктов и является параллельным [1, 4], что позволяет ускорить процесс прогнозирования и эффективно использовать вычислительные ресурсы современных многопроцессорных и многоядерных систем.

Найденные базовые факты могут быстро указать причину, по которой прогноз закончился неудачей или его результат получился некорректным.

Рецензенты:

Вечтомов Е.М., д.ф.-м.н., профессор, зав. кафедрой «Алгебра и дискретная математика», ГОУ ВПО «ВятГГУ», г. Киров;

Окулов С.М., д.п.н., профессор, декан факультета «Информатика, математика и физика», ГОУ ВПО «ВятГГУ», г. Киров.

Работа поступила в редакцию 21.12.2012.

Библиографическая ссылка