Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Никитин О.Р. 1 Горшков К.А. 1 Али Аббас Мохсин Али 1 Рау Т.Ф. 1 Рау В.Г. 1

---

1 ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых»

Знание структуры элемента радиосхемы или синхрогруппы в сети в условиях радиации становится необходимым. В работе впервые приведены примеры перестройки нанокластеров в устройствах, состоящих из атомов с радиоактивными ядрами, поскольку стабильность существования и функционирования устройств напрямую зависит от устойчивости их компонентов. Рассмотрено влияние радиоактивных превращений на симметрию наночастиц, которые могут выполнять функцию элементов сетей. Показана необходимость учета влияния радиации на все элементы устройств на наноуровне и проведения дополнительных расчетов устойчивости атомно-молекулярных систем с определением вероятности изменения свойств таких систем. Для проведения таких расчетов в работе использованы результаты компьютерного моделирования нанокластеров на основе данных рентгенодифракционного анализа по методике послойного роста структур. Впервые введено понятие радиоактивных нанокластеров для случая, когда ядра кластеров одного изотопного состава превращаются в другие.

Статья в формате PDF

722 KB

радиотехнические сети и устройства

элементы сети

нанотехнологии

радиоактивные нанокластеры

превращения нанокластеров

1. Варламов В.В., Ишханов Б.С., Комаров С.Ю. Атомные ядра. Основные характеристики: учебное пособие. – М.: Университетская книга, 2010. – 334 с.

2. Горшков К.А., Никитин О.Р., Рау Т.Ф., А.А. Мохсин Али, Рау В.Г. Комбинаторно-геометрический метод расчета и представления вариантов конфигураций дерева графа сетевых доменов // Журнал «Современные проблемы науки и образования». – 6, выпуск РАЕ. – М., 2013. URL: http://www.science-education.ru/113-11297.

3. Краснок А.Е., Максимов И.С. Денисюк А.И., Белов П.А., Мирошниченко А.Е., Симовский К.Р., Кившарь Ю. С. Оптические наноантенны // УФН. – 2013. – Т. 183, № 6. – С. 561–589.

4. Никитин О.Р., Скворцов К.В., Рау Т.Ф., Малеев А.В., Рау В.Г.. Моделирование фрактальных структур, антенн и излучателей для нанотехнологий. // Известия института инженерной физики. – Серпухов, 2010 – № 1, (15) – С. 61–65.

5. Рау В.Г., Журавлев В.Г., Рау Т.Ф., Малеев А.В. Морфогенез кристаллических структур в методе дискретного моделирования упаковок. // Кристаллография. – 2002. – Т. 47, № 5. – С. 793–796.

6. Martin T.P, Bergmann T., Gohlich H. and Lange T. Evidence for icosahedral shell structure in large magnesium clusters.// Journal of Chemical Physics. – 1991. – № 176. – P. 343.

При классификации сетей на основе их геометрической структуры и топологии в работе [2] нами было выделено три наиболее различающиеся между собой случая:

1. Распределение элементов сети в пространстве неоднородно и сами элементы обладают различными радиофизическими свойствами (характеристиками). Такую сеть будем называть неупорядоченной.
2. Сеть создается по проекту без привязки к особенностям рельефа местности, например, в космическом пространстве. В этом случае можно упорядочить структуру (в зависимости от различных требований), сделать, например, однородной, то есть наиболее симметричной, что выгодно даже исходя из экономических соображений. Такая сеть названа полностью или глобально упорядоченной. Геометрическим примером глобально упорядоченной сети является правильная решетка трансляций, связывающая элементы синхрогруппы маршрутизации;
3. Третий вариант представляет собой сочетание локально неупорядоченной структуры с глобальной упорядоченностью. В качестве основного объекта исследования в данной работе выберем именно такой вариант сети: решетка трансляций с фундаментальной областью, заполненной неупорядоченными доменами (терминология обсуждена в работе [2]. Сеть в этом случае названа локально неупорядоченной. Пример такой сети представлен на рис. 1.

Крупные элементы синхрогруппы на рисунке определяют глобальную упорядоченность (трансляционную ячейку), мелкие элементы связаны друг с другом неупорядоченно и образуют вершины графа маршрутизации сети, а отрезки (ребра графа) определяют маршрутизацию сети. Каждый элемент синхрогруппы, расположенной в вершинах графа маршрутизации, представляет собой передающее и принимающее радиоустройство или просто ретранслятор в виде управляемой антенны.

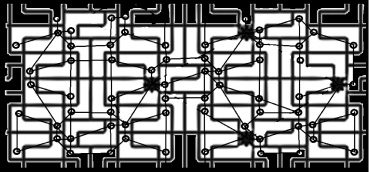
Рис. 1. Пример локально неупорядоченной сети

В любом случае при работе сети возникает проблема радиационной защищенности этого устройства. В области новых технологий поведение радиосистем в условиях повышенной радиации становится слабо прогнозируемым. Как при создании новых материалов для ядерной энергетики, так и при разработке входящих в радиосистему электронных приборов, защищенных от радиации, знание структуры элемента синхрогруппы становится, на наш взгляд, почти необходимым. Последнее время в качестве антенн используются наноустройства, представляющие собой управляемую систему в микро- и наномире [4, 3]. Проблемы устойчивой работы любой схемы и любой радиосети в этом случае практически не зависят от размеров их конструкции. В любом случае опасные ядерные частицы и космическое радиационное излучение изменяют структуру вещества, нарушают свойства нанокластеров.

Цель исследования – изучение влияния радиации на элементы устройств на наноуровне и на изменение функционирования этих устройств и систем.

Результаты исследования и их обсуждение

Если вещество само состоит из радиоактивных изотопов, то происходит его превращение: ядра кластеров одного изотопного состава превращаются в другие, поэтому можно говорить о существовании радиоактивных нанокластеров. Эти изменения кластеров при любых радиоактивных превращениях могут менять симметрию наночастицы и ее свойства. Ниже приведем один из таких примеров. Рассмотрим вначале радиационную составляющую процессов, их последовательность, используя табличную информацию, приведенную, например, в работе [1]. В качестве примера выберем стабильный изотоп кадмия-114 (с распространенностью 28,7 %), поглощающий как нейтроны, так и протоны в соответствии с приведенными ниже реакциями.

1.

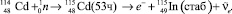
2.

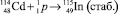
3.

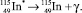
Очевидно, что как в первой реакции, так и во второй происходит «трансмутация» кластеров кадмия в кластеры стабильного индия.

Превращение кадмия в индий (табл. 2) кардинально меняет симметрию кластера. Тем не менее после проведения соответствующего наноструктурного исследования оказалось, что с точки зрения координационного подхода, а следовательно, и магических чисел, индий (при k = 1) является кластерным топологическим изомером кубооктаэдра. Компьютерное моделирование нанокластеров на основе данных рентгенодифракционного анализа (РДА) проведем по методике послойного роста структур, представленной ранее в работе [5].

Кластеры исходного продукта кадмия строятся по связям (ближайшим «контактам») в твердотельной структуре. Исходная информация (международный банк минералов «WWW-MINCRYST»): координаты атомов в ячейке с симметрией федоровской группы и межатомные (межъядерные) расстояния в первой координационной сфере каждого атома приводятся ниже (табл. 1).

Таблица 1

Кристаллоструктурные данные кадмия

Как показывает расчет для трех изоструктурных ячеек кадмия, цинка и магния, нанокластеры их также изоструктурны и приведены на рис. 2.

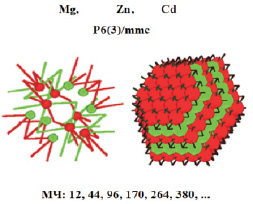
Рис. 2. Нанокластеры магния, цинка и кадмия с одинаковым набором магических чисел

Если обратить внимание на результаты масс-спектроскопии магния (для кадмия и цинка такая информация отсутствует), то количество атомов на k-й «оболочке» поверхности устойчивых нанокластеров магния, полученных в эксперименте [6], соответствуют закону последовательности чисел 10k2 + 2 (12, 42, 92, 162,…), а при расчете нанокластера магния, основанном на результатах РДА (рис. 2, МЧ), в каждом слое появляются дополнительные числа, что указывает на различие этих типов структур.

В литературе [6] для объяснения результатов масс-спектроскопического эксперимента обсуждаются только 2 варианта нанокластеров: в формах икосаэдра или кубического кубооктаэдра. В то же время легко найти преобразование симметрии (ось поворота, проходящая через центры параллельных треугольных граней), которая переводит один многогранник в другой. Но симметрия кристаллического магния не удовлетворяет ни одному из этих вариантов. Возможно существование гексагональной формы «кубооктаэдра» с тем же набором магических чисел, который также может быть получен той же операцией вращения, производимой до тех пор, пока параллельные плоскости кубооктаэдра не будут связаны плоскостью симметрии. Не вникая в подробности такого несогласия моделей (что соответствует по объему материала еще одной полной статье), можно остановиться на варианте икосаэдрической симметрии (рис. 3, слева) до тех пор, пока не будут проведены дополнительные исследования. Для процессов, которые рассматриваются в этой статье, вопрос не является принципиальным до момента сборки наносистемы в реальности.

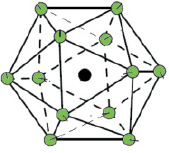
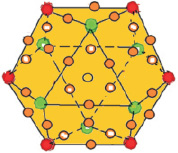
Рис. 3. Атомы на поверхностях икосаэдра с k = 1 (первая оболочка, слева) и кубооктаэдра с k = 2 (вторая оболочка, справа)

Таблица 2

Кристаллоструктурные данные индия

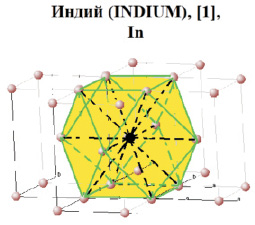
Рис. 4. Нанокластер индия (k = 1)

Выводы

Поиск материалов, атомы и ядра в которых стабильны, определяет стабильность существования устройств, из которых они сделаны. Но так как абсолютно стабильных веществ не существует, то необходимо проводить дополнительные расчеты устойчивости атомно-молекулярных систем и заранее определять вероятности изменений свойств и функций, выполняемых этими устройствами. Так, например, бытующее в нанотехнологии мнение о бездефектности графена в этом смысле несостоятельно. Известно, что в каждом веществе, содержащем углерод, небольшая доля радиоактивного ядра С-14 (большой период полураспада) присутствует всегда. При радиоактивном превращении ядра углерода в азот:

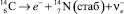в графеновой гексагональной сетке появится дефект, несмотря на большой период полураспада ядра С-14. Появление атома азота в графене изменит и его свойства.

Работа поддержана грантом РФФИ № 14-02-97504.

Рецензенты:

Поздняков А.Д., д.т.н., профессор, ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых», г. Владимир;

Полушин П.А., д.т.н., профессор, ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых», г. Владимир.

Работа поступила в редакцию 26.03.2014.

Библиографическая ссылка