Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лайпанова А.М. 1 Желдашева А.О. 2 Лесев В.Н. 2

---

1 Московский государственный университет путей сообщения

2 ГОУ ВПО «Кабардино-Балкарский государственный университет им. Х.М. Бербекова»

В работе поставлена и исследована краевая задача типа задачи Франкля для обобщенного смешанного уравнения параболо-гиперболического типа с переменными коэффициентами при младших членах в конечной односвязной области. Для исходной задачи была сформулирована и доказана методом «abc» теорема единственности. Выполнение условий этой теоремы обеспечивает тривиальность соответствующей однородной задачи, что и гарантирует единственность решения исследуемой краевой задачи в целом. Доказательство существования явного аналитического решения задачи проведено для одного частного случая исходного уравнения. При этом были использованы метод функций Грина и метод интегральных уравнений. В результате определены условия, при которых вопрос разрешимости задачи в требуемом классе функций может быть эквивалентно редуцирован к вопросу разрешимости соответствующего интегрального уравнения.

Статья в формате PDF

1189 KB

задача Франкля

смешанное уравнение

метод «abc»

однозначная разрешимость

1. Елеев В.А., Лайпанова А.М. О существовании и единственности решения задачи Ф.И. Франкля для смешанного уравнения гиперболо-параболического типа // Известия КБНЦ РАН. – 2000. – № 2 (5). – С. 50–56.

2. Елеев В.А., Лесев В.Н. О двух краевых задачах для смешанных уравнений с перпендикулярными линиями изменения типа // Владикавказский математический журнал. – 2001. – Т. 3. – № 4. – С. 9–22.

3. Лайпанова А.М., Лесев В.Н. Об однозначной разрешимости краевой задачи для модельного уравнения второго порядка // Сборник научных трудов Северо-Кавказского государственного технического университета. Серия: Естественные науки. – 2007. – С. 31.

4. Лесев В.Н., Желдашева А.О. Неклассическая краевая задача для смешанного модельного уравнения второго порядка с нелокальными условиями сопряжения // Сборник научных трудов Sworld. – 2012. – Т. 2. – № 3. – С. 99–104.

5. Лесев В.Н., Желдашева А.О. Неклассическая краевая задача для смешанного уравнения второго порядка с интегральными условиями сопряжения // Известия Смоленского государственного университета. – 2013. – № 3 (23). – С. 379–386.

6. Псху А.В. Задачи Франкля для уравнений смешанного типа: автореф. канд. дис. ... – Нальчик: НИИ ПМА КБНЦ РАН, 1999.

7. Смирнов М.М. Уравнения смешанного типа. – М.: Высшая школа, 1985. – 304 с.

В связи с появлением все новых приложений уравнений смешанного типа теория краевых задач для них в последние годы получила новый импульс развития. При этом существенную роль в приложениях занимают краевые задачи для параболо-гиперболических уравнений (например [1–5]), отличающиеся от иных в первую очередь специальными методами, применяемыми при их исследовании. Говоря о задаче Франкля и ее аналогах для смешанных параболо-гиперболических уравнений, следует отметить, что их изучение не носит систематического характера, несмотря на значительную важность подобных исследований [6].

В настоящей работе представлено доказательство единственности решения аналога задачи Франкля для смешанного параболо-гиперболического уравнения с переменными коэффициентами, а также доказано существование частного аналитического решения.

Постановка задачи

Рассмотрим уравнение

(1)

в конечной односвязной области Ω евклидовой плоскости независимых переменных x, y, ограниченной отрезком A′A оси x = 0; –1 ≤ y ≤ 1; отрезками B′B, AB прямых x = ℓ, y = 1; характеристикой A′C_m:

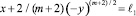
уравнения (1), где A′(0, –1), C(ℓ₁, 0) ℓ₁ ≤ ℓ и отрезком CB′ оси x, ℓ₁ ≤ x ≤ ℓ, ℓ₁ = 2/(m + 2).

Обозначим через 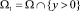; OP – часть характеристики уравнения (1), исходящей из точки O(0,0) до пересечения с A′C в точке P; Ω₂ – область, ограниченная кривыми OP, PC и OC; Ω₃ – область, ограниченная кривыми OA′, A′P и PO.

Относительно коэффициентов уравнения (1) предполагается, что

,

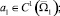
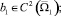
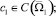
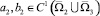причем b1(x, y) < 0, c1(x, y) ≤ 0, a1(x, y) ≤ 0, b2(x, y) ≤ 0.

Задача Ф. Требуется найти функцию u(x, y) со следующими свойствами:

1)

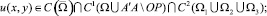
2) Lu(x, y) = 0, ;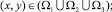

3) u(x, y) удовлетворяет краевым условиям:

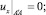(2)

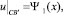ℓ1 ≤ x ≤ ℓ; (3)

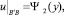0 ≤ y ≤ 1; (4)

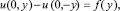–1 ≤ y ≤ 1, (5)

где Ψ₁(x), Ψ₂(y), f(y) – заданные функции, удовлетворяющие условию Гельдера.

Доказательство единственности решения задачи Ф

Покажем, что однородная задача Ф (Ψ₁ = Ψ₂ = f = 0) имеет только нулевое решение.

Справедлива следующая

Теорема 1. Пусть коэффициенты уравнения (1) удовлетворяют условию

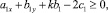
где

.

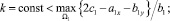
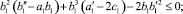
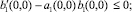
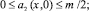
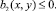Тогда решение u(x, y) однородной задачи Ф в области Ω тождественно равно нулю.

Для доказательства теоремы 1 применим метод «abc». Умножим уравнение (1) на выражение

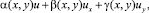
где α, β, γ – пока произвольные достаточно гладкие функции, и проинтегрируем полученное соотношение по области Ω.

В результате, принимая во внимание, что u_x = x_nu_n, u_y = y_nu_n на B′B, где x_n и y_n − направляющие косинусы внешней нормали 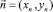к границе области Ω, 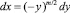на характеристике A′C и учитывая однородные граничные условия, приходим к равенству

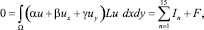(6)

где I_n – интегралы от искомой функции, а F – слагаемые, содержащие квадраты искомой функции в явном виде.

Выбирая функции α, β, γ таким образом, чтобы все интегралы I_n в (6) были неотрицательны. Для этого достаточно положить в Ω₁ α = –exp(ky); β = 0, γ = 0, а в Ω_i, i = 2, 3,

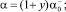
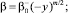
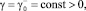
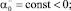
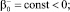
где 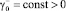таковы, что выполняются неравенства:

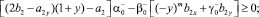
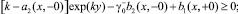
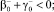
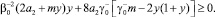
Тогда нетрудно убедиться в том, что при выполнении условий теоремы 1, u ≡ 0 в Ω. Следовательно, в силу тривиальности решения однородной задачи решение задачи Φ единственно.

Доказательство существования решения задачи Ф

Проведем доказательство существования решения для случая

a₁ = c₁ = a₂ = b₂ = 0,

b₁ = –1.

Решение уравнения (1) при y < 0, удовлетворяющее условиям Коши

u(x, 0) = τ(x),

u_y(x, 0) = v(x),

имеет вид 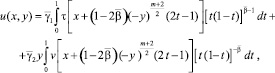[7]:

(7)

где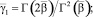

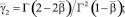
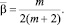
Учитывая условие (6), получим соотношение между τ(x), v(x), φ(y) = u(0, y), 0 ≤ y ≤ 1. Для этого положим в равенстве (7) x = 0, затем заменим (–y) на 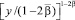, полученное выражение умножим на 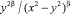, проинтегрируем по y от 0 до x и, наконец, продифференцируем полученное равенство по x. Получим

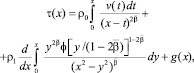(8)

где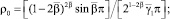

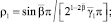
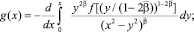
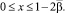
Решая в параболической части Ω₁ смешанную задачу u_x(0, y) = 0, u(x, 0) = τ(x), u(ℓ, y) = Ψ₂(y) для уравнения (1) при y > 0, получим

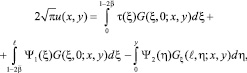(9)

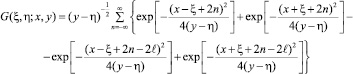где (10)

– функция Грина смешанной задачи уравнения теплопроводности.

Полагая в (9) x = 0 и учитывая условие (2) после замены переменной ξ по формуле 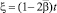в первом интеграле, получим

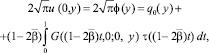(11)

где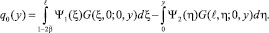

В равенстве (11) y заменим через 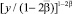, затем умножим обе части на 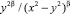и проинтегрируем от 0 до x по переменной y и, наконец, полученное выражение продифференцируем по x, получим

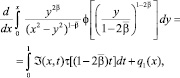(12)

где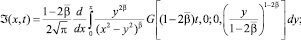

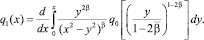
В силу свойств функции Грина (10) и заданных функций Ψ1(x), Ψ2(y) заключаем, что

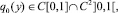
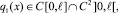
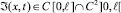
по переменным x и t.

Исключая φ(y) из (8) и (12), будем иметь

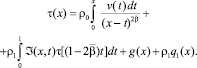(13)

Решая задачу: 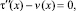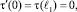получим соотношение между τ(x) и v(x) на линии y = 0 из параболической части Ω₁ в виде

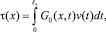(14)

где G₀(x, t) – функция Грина.

Подставим значение τ(x) из (14) в (13)

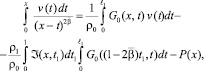(15)

где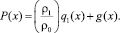

Обозначая правую часть уравнения (15) через ρ(x) и обращая полученное уравнение Абеля, будем иметь

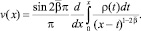(16)

Возвращаясь от ρ(x) к v(x) и P(x), в результате элементарных преобразований, получим интегральное уравнение Фредгольма второго рода относительно v(x):

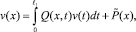(17)

где Q(x, t) и 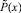выражаются через заданные функции.

Таким образом, в силу единственности решения задачи Φ убеждаемся в однозначной разрешимости уравнения (17).

Определив из (17) v(x), а затем по формуле (15) и τ(x), находим решение задачи Φ в области Ω₁, которое будет иметь вид (9), а в области Ω₂ – вид (7). В области Ω₃ решение задачи Φ можно продолжить как решение задачи Дарбу.

Заключение

В работе установлены единственность решения нелокальной краевой задачи для смешанного уравнения второго порядка в замкнутой области. Для доказательства единственности решения применен метод «abc». Доказательство существования частного решения поставленной задачи проведено на основе методов функции Грина и интегральных уравнений.

Рецензенты:

Журтов А.Х., д.ф.-м.н., профессор, заведующий кафедрой ГиВА, КБГУ им. Х.М. Бербекова, г. Нальчик;

Хаширова Т.Ю., д.т.н., профессор кафедры ИМОАС, КБГУ им. Х.М. Бербекова, г. Нальчик.

Работа поступила в редакцию 28.07.2014.

Библиографическая ссылка