Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

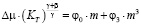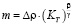, , (1)

где 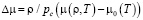; ; 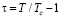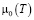– регулярная функция температуры; pc – критическое давление; Tc – критическая температура; T – абсолютная температура; ρ – плотность; β и γ – соответственно критические индексы кривой сосуществования x = – x₀ и коэффициента изотермической сжимаемости K_T; φ₀ и φ₃ – постоянные коэффициенты; 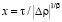– масштабная переменная; 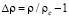; p_c – критическая плотность; x₀– параметр, определяющий поведение кривой сосуществования данного вещества в асимптотической окрестности критической точки.

Выражение для K_T выберем исходя из гипотезы об одинаковом характере поведения изотермической сжимаемости на критической и околокритических изохорах [10]:

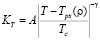, (2)

где A – амплитуда; T_ps(ρ) – линия особых точек изотермической сжимаемости (спинодаль).

В асимптотической окрестности критической точки, так как 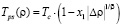, имеем из (2):

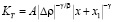, (3)

где x₁ – постоянный параметр.

Из уравнения состояния (1), подставляя в него (3), получим искомое масштабное уравнение в переменных плотность-температура [2]:

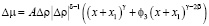, (4)

где δ – критический индекс критической изотермы.

Из (4) непосредственно следует, что масштабная функция химического потенциала 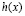в рамках рассматриваемого подхода к описанию критических явлений имеет вид:

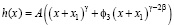. (5)

На линии фазового равновесия x = – x₀ должно выполняться равенство 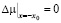, а следовательно, и

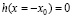. (6)

Найдем из (6) значение параметра ϕ3:

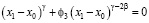
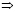
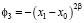. (7)

Подставим найденное значение ϕ₃ в (2) получим выражение для масштабной функции 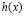, содержащее два подгоночных параметра: A – амплитуду и x₁ – индивидуальный параметр, который определяет на термодинамической поверхности, как будет ниже показано, линию сингулярности изохорной теплоемкости C_v.

С целью установить значение параметров A и x₁, воспользуемся линейной моделью [3]:

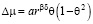, (8)

где независимые переменные r и θ соответственно характеризуют «расстояние» до критической точки и угол поворота относительно критической изохоры; a – индивидуальная постоянная вещества. Переменные r и θ связаны с ρ и T зависимостями:

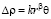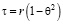и , (9)

где .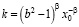

Масштабная функция химического потенциала 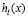, соответствующая (8) и (9), имеет вид [3]:

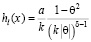. (10)

Потребуем, чтобы вблизи критической изохоры выполнялся предельный переход:

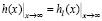. (11)

Так как

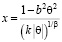, (12)

где 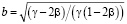, то функцию (10) можно представить в виде

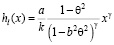. (13)

Учитывая, что на критической изохоре θ = 0, получим из (11) равенство

A = a / k. (14)

Таким образом, в функции (5) остался один неопределенный параметр x1.

С целью установить значение x1 воспользуемся равенством:

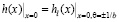(15)

и, подставляя в (15) зависимости (5) и (13), придем к уравнению:

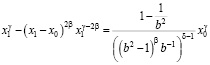. (16)

Сделаем в (16) замену 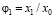и получим

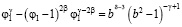. (17)

Из уравнения (17) найдем искомое значение параметра φ₁. Обратим внимание на то, что параметр φ₁ является универсальным с точностью до универсальности критических индексов. Решая уравнение (17) найдем значение φ₁ = 52,751, а следовательно:

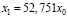. (18)

Для того, чтобы оценить точность предложенной модели масштабного уравнения (4), найдем значения 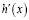, , 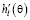а также масштабные функции изотермической сжимаемост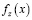и и .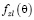

Производная масштабной функции химического потенциала ЛМ имеет вид [3]:

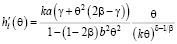. (19)

Производная масштабной функции химического потенциала, рассчитанная на основе (5), описывается выражением:

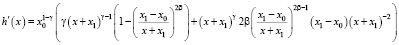, (20)

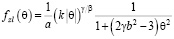. (21)

Масштабная функция изотермической сжимаемости, в случае (4), рассчитывается путем подстановки в формулу:

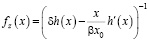, (22)

выражений (5) и (20).

Обратим внимание на то, что согласно (5), (20) и (22) на линии x = – x₁ выполняется равенство

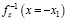=0 .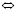

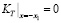
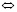
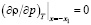Следовательно, уравнение x = – x₁ описывает линию псевдокритических точек – линию сингулярности изохорной теплоемкости, положение которых на термодинамической поверхности определяется системой равенств [8]:

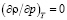
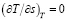(23)

На рис. 1 представлено сравнение предложенной модели и ЛМ. Отклонения между значениями (5) и (10), (20) и (19), (22) и (21) представляются слишком большими.

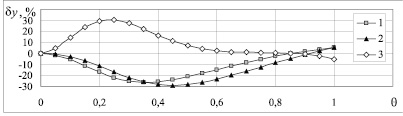
Рис. 1. Относительные отклонения масштабных функций данной работы (5), (20) и (22) от масштабных функций линейной модели (10), (19) и (21), соответственно: 1 – химического потенциала; 2 – производной химического потенциала; 3 – изотермической сжимаемости

Установим, насколько данное выражение является гладким на критической изохоре. Пусть ∆ρ → 0, тогда из (4) имеем:

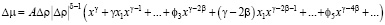. (24)

Из (24) следует, что при x → ∞ поведение масштабной функции (5) описывается зависимостью:

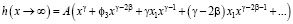. (25)

В то же время, в случае линейной модели имеем:

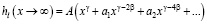, (26)

где a_i – постоянные ().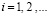

Из (24) и (25) следует, что если первые два члена разложения по степеням x совпадают, поведение третьих слагаемых носит качественно разный характер:

, .

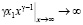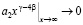Таким образом, аналитические характеристики масштабной функции (5) можно улучшить, если исключить из разложения по степеням x в (24) слагаемое γx₁x^γ-1.

С этой целью воспользуемся методом псевдокритических точек [13] (известным также как метод нескольких псевдоспинодальных кривых [2, 10]) и преобразуем (5) к следующему виду:

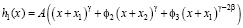. (27)

Теперь разложение по степеням x функции (27) при x → ∞ выглядит так:

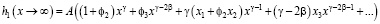. (28)

Для того, чтобы добиться требуемого разложения масштабной функции h1(x) по степеням x, наложим на параметры x₁, x₂, ϕ2 условие 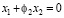, в результате получим:

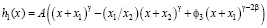. (29)

Для того, чтобы удовлетворить требованию равенства химических потенциалов на паровой и жидкостной ветвях линии насыщения, выберем значение параметра ϕ₃ из условия :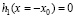

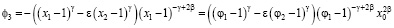, (30)

где , .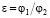

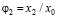Подставим найденное значение ϕ₃ в (27), и, выполнив замену переменной x на ϕ, в результате получим следующее выражение h₁(x):

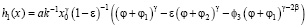. (31)

Для определения значений параметров φ₁ и φ₂ воспользуемся равенствам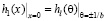и:

и 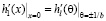. (32)

Функция h'₁(x) имеет вид:

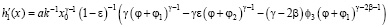. (33)

Подставим масштабные функции (10), (19), (31) и (33) в равенства (32) и получим искомую систему уравнений:

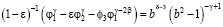, (34)

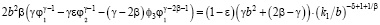. (35)

Решая совместно уравнения (34), (35) получим следующие значения параметров 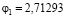и .

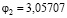Масштабная функция изотермической сжимаемости, в случае (31) и (33), имеет вид:

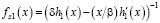. (36)

Представленные на рис. 2. отклонения между масштабными функциями (31), (33) и (36) и соответствующими функциями линейной модели (10), (19) и (21) значительно меньше, чем отклонения масштабных функций (5), (20) и (22) от ЛМ.

Заключение

Полученное в данной работе масштабное уравнение состояния по своим расчетным характеристикам не уступает известным масштабным уравнениям в параметрической форме и может быть использовано при построении единых и широкодиапазонных уравнений состояния [1, 11], используемых для описания как регулярной части термодинамической поверхности, так и околокритической и метастабильной области и структурно включающих линию насыщения [15] в качестве опорной кривой.

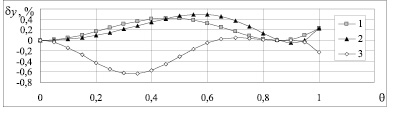
Рис. 2. Относительные отклонения масштабных функций (31), (33) и (36) от масштабных функций линейной модели (10), (19) и (21), соответственно: 1 – химического потенциала; 2 – производной химического потенциала; 3 – изотермической сжимаемости

Рецензенты:

Борзенко Е.И., д.т.н., профессор, зав. каф. криогенной техники ИХиБТ НИУ ИТМО, г. Санкт-Петербург;

Цветков О.Б., д.т.н., профессор, зав. каф. теоретических основ тепло- и хладотехники ИХиБТ НИУ ИТМО, г. Санкт-Петербург.

Работа поступила в редакцию 14.08.2014.