Механические приводы, создаваемые на основе известных модификаций зубчатых цилиндрических и конических передач, червячных и планетарных передач, потребностям, предъявляемым нефтегазовой отраслью, в ряде случаев не соответствуют. Есть необходимость в редукторах с высоким коэффициентом полезного действия, низкими массогабаритными показателями, малыми страгивающими моментами, что обусловлено условиями эксплуатации приводов в районах Крайнего Севера. Эффективным направлением решения проблемы является разработка нового поколения приводов [8, 9] на базе прецессирующей плоскоконической передачи (ППКП). При малой разнице чисел зубьев шестерни и колеса, приводы на основе ППКП [6, 7, 10], могут быть изготовлены с передаточным отношением от 10 до 65, их радиальные габариты по сравнению с традиционными приводами значительно меньше при высоком коэффициенте полезного действия (η ≈ 0,9). В ППКП реализуется многопарное зацепление зубьев, вследствие чего нагрузочная способность приводов с ППКП другие их виды значительно превышает. На рис. 1 и рис. 2 показаны привод шарового крана ДУ-300 и редукторная вставка винтового насоса для добычи тяжелых нефтей, в конструкциях которых использована ППКП.
В работах [3, 4, 5] рассмотрены особенности геометрии ППКП, построены математические модели процесса формообразования зубьев колес, решены задачи определения оптимальных геометрических характеристик зацепления зубьев в передаче на основе варьирования параметров инструментов и наладок зуборезного станка. В то же время для проектирования приводов, содержащих ППКП, необходимо уметь оценивать нагруженность многопарного зацепления зубьев колес передачи, необходимую для расчета величины крутящего момента передаваемого ППКП исходя из условия обеспечения контактной и изгибной прочности элементов передачи. Решение данной задачи представлено в настоящей статье.
Рис. 1. Привод шарового крана
Рис. 2. Редукторная вставка
Методика расчета распределения нагрузки между парами зубьев в плоскоконической передаче
Отличительная особенность ППКП заключается в том, что поверхности зубьев пар, соседних с контактирующей парой, в любой фазе зацепления расположены достаточно близко, и с приложением к передаче внешнего крутящего момента реализуется многопарность зацепления. С позиций механики, рассматриваемая передача является упругой системой с односторонними упругими связями (зубьями), поскольку эти связи воспринимают нагрузку лишь одного знака (контактирующие поверхности зубьев только сжимаются). Более того, плоскоконическая передача представляет собой систему с изменяемой структурой, поскольку с изменением величины передаваемого крутящего момента изменяется число связей, воспринимающих этот крутящий момент в секторе нагруженных пар зубьев.
Определение нагруженности многопарного зацепления представляет собой задачу раскрытия статической неопределимости системы с односторонними связями [1, 2], в процессе решения которой устанавливается число контактирующих пар, воспринимающих заданную нагрузку (крутящий момент) и характер распределения ее по этим парам.
Задача расчета распределенной нагрузки между контактирующими парами зубьев плоскоконической передачи формулируется следующим образом. В ненагруженном состоянии между зубьями колеса и шестерни имеются зазоры δSi, причем для i = 1 зазор δS1 минимален. После приложения крутящего момента T1 к шестерне, имеющей число зубьев z1, в контакт вступит n-ая пара зубьев из z1. Требуется найти число пар зубьев n, воспринимающих заданный крутящий момент T1, и определить характер распределения T1 между парами зубьев плоскоконической передачи, для чего необходимо решить систему двух уравнений, одно из которых является уравнением равновесия, а второе –уравнение совместности деформаций и перемещений [1]:
;
; 
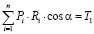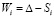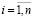. (1)
Здесь Pi, Ri – нормальная сила и радиус ее действия на i-ой паре зубьев; α – угол зацепления; Si – зазор между поверхностями в i-ой паре зубьев, рассчитываемый по выражению: Si = δSi – δS1 (отметим, что зазор на первой паре δS1 «выбирается» без какого-либо деформирования зубьев, путем поворота шестерни вокруг оси вращения); ∆ – сближение зубчатых колес, являющееся мерой упругого деформирования зубчатой передачи; Wi – деформация i-ой пары зубьев.
Следуя работе [1], для передач с пространственным зацеплением зубьев деформацию Wi в зависимости от нагрузки Pi, действующей по нормали к контактирующим поверхностям, представим в виде двухчленной зависимости:
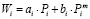, (2)
где ai – податливость i-ой пары зубьев, вызываемая их изгибом; bi – коэффициент, характеризующий контактную податливость i-ой пары зубьев; m = 2/3 – показатель степени зависимости, полученной Герцем для расчета сближения упругих тел в случае их точечного начального касания.
При касании первой пары зубьев S1 = 1, поэтому из (1) следует, что ∆ = W1. Запишем далее уравнение совместности деформаций и перемещений для i-ой и n-ой пары зубьев:
, 
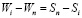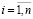. (3)
Пусть при крутящем моменте T в контакт вступила n-ая пара зубьев, но нагрузку эта пара еще не воспринимает, в этом случае Wn = 0. Определим зазор Si в i-ой паре в виде: Si = S0∙Fi, где S0, Fi – соответственно амплитуда и функция зазоров между зубьями, зависящие от геометрических особенностей исследуемой передачи. С учетом изложенного, второе уравнение системы (1), преобразуется к виду:
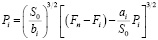. (4)
Решение данного трансцендентного уравнения при фиксированных значениях n относительно Pi позволяет определить величину нагрузки, воспринимаемой каждой контактирующей парой зубьев и по первому из уравнений системы (1) рассчитать передаваемый крутящий момент.
Рассмотрим пример определения характера распределения нагрузки между парами зубьев плоскоконической передачи привода шарового крана (рис. 1), передаточное отношение которого u = 65. Параметры передачи: число зубьев шестерни z1 = 64, число зубьев колеса z2 = 65, нормальный модуль mn = 5 мм. Методика расчета геометрических параметров передачи изложена в работе [5]. Используя программный комплекс по исследованию геометрических характеристик зацепления зубьев плоскоконической передачи [4], были определены значения Si для трех фаз зацепления: φ = – 0,01; – 0,06; – 0,11. Аппроксимация результатов расчета позволила представить Si в виде
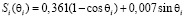, (5)
где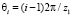 
– угол, задающий расположение зуба на зубчатом венце (i = 2,3,4…), и описать функцию зазоров Fn – Fi зависимости (4) в форме
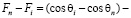
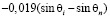. (6)
Функция (5) для исследуемой передачи представлена на рис. 3.
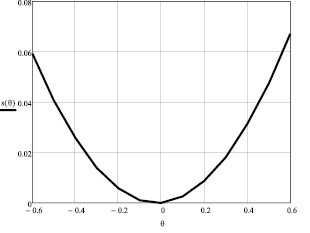
Рис. 3. Изменение минимального зазора между контактирующими парами зубьев
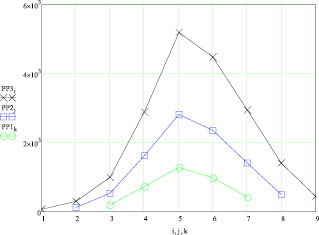
Рис. 4. Распределение нагрузки в зацеплении колеса и шестерни плоскоконической передачи в зависимости от числа пар зубьев, участвующих в передаче крутящего момента
Входящие в выражение (4) параметры S0, ai и bi определим на основе обработки результатов, представленных в работах [1, 2]. Следуя им, для стальных колес получены значения: S0 = 0,361 мм; bi = 1,4222∙10-4. Для вычисления коэффициента ai, учитывая, что для положительных и отрицательных фаз зацепления распределение нагрузки по фазам является несимметричным, использованы следующие аппроксимирующие зависимости:
для i < 0; i = 2,3,… ai = 0,061∙10-5 + (4,104∙ ∙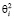
+ 48,499∙
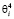)∙10-4, мм/Н;
для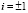 
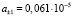, мм/Н; (7)
для i > 0; i = 2,3,… ai = 0,061∙10-5 + (0,422∙ ∙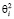
+ 4,203∙
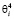)∙10-4, мм/Н.
В результате реализации разработанной методики расчета нагрузки, воспринимаемой парами зубьев плоскоконической передачи для n = 4, 5 и 6, получены величины Pi, показанные на рис. 4. На основании первого из уравнений системы (1) были рассчитаны значения крутящего момента передачи при n = 4, 5 и 6: T = 3287,9; 8518, 8; 17080,0 Н∙М, позволяющие оценить нагрузочную способность исследуемой плоскоконической передачи, с учетом многопарности контакта зубьев в зацеплении колеса и шестерни.
Заключение
Для многопарного контакта зубьев плоскоконической передачи разработана методика расчета нагрузки, распределенной между контактирующими парами зубьев. Методика учитывает как величину минимального зазора между поверхностями контактирующих зубьев, так и их податливость при передаче крутящего момента. Представлен пример расчета нагруженности плоскоконической конической передачи изготовленного привода, позволяющий в зависимости от числа пар зацепления в передаче определить для привода величину внешнего крутящего момента.
Рецензенты:
Лопатин Б.А., д.т.н., профессор, заведующий кафедрой «Техническая механика», ФГБОУ ВПО «Южно-Уральский государственный университет» (национальный исследовательский университет), филиал ЮУрГУ в городе Златоусте, г. Златоуст;
Трубачев Е.С., д.т.н., профессор, и.о. заведующего кафедрой «Конструкторско-технологическая подготовка машиностроительных производств», ФГБОУ ВПО «Ижевский государственный технический университет им. М.Т. Калашникова», г. Ижевск.
Работа поступила в редакцию 30.12.2014.
Библиографическая ссылка
Сызранцев В.Н., Пазяк А.А. РАСЧЕТ НАГРУЗКИ В ЗАЦЕПЛЕНИИ ЗУБЬЕВ КОЛЕС ПЛОСКОКОНИЧЕСКОЙ ПЕРЕДАЧИ // Фундаментальные исследования. 2014. № 12-11. С. 2320-2324;URL: https://fundamental-research.ru/ru/article/view?id=36688 (дата обращения: 02.04.2025).