Цель исследования – рассмотрение сущностных характеристик дифференцированного обучения учащихся 7–9 классов решению текстовых задач алгебраическим методом.
Материалы и методы исследования
Для решения поставленных задач и проверки исходных положений в исследовании был использован комплекс методов: методы педагогического конструирования; теоретический анализ и обобщение педагогических, психологических, методических трудов по проблеме исследования; изучение и обобщение инновационного педагогического опыта; педагогический эксперимент.
Результаты исследования и их обсуждение
Проблема дифференциации обучения не нова для отечественной науки и практики. В работах Ю.К. Бабанского, М.А. Данилова, Б.П. Есипова, Н.М. Шахмаева и др. обосновано, что дифференцированный подход является одним из основных условий повышения качества обучения, раскрыты теоретические основы его реализации. Различными исследователями в качестве существенных признаков дифференциации обучения выделяются следующие: учет индивидуальных различий обучающихся (Г.Д. Глейзер, И.М. Чередов, Н.М. Шахмаев и др.); целесообразность группирования учащихся на основе доминирующих особенностей (Е.С. Рабунский, И.Э. Унт и др.); вариативность процесса обучения по формам, методам, приемам обучения, по содержанию, уровню усвоения математического содержания и т.д. (В.А. Гусев, М.И. Зайкин, Г.И. Саранцев и др.).
Г.В. Дорофеев, Л.B. Кузнецова, С.Б. Суворова под дифференциацией понимают такую систему обучения математике, при которой каждый обучающийся, овладевая некоторым минимумом общеобразовательной подготовки, являющейся общезначимой и обеспечивающей возможность адаптации в постоянно изменяющихся жизненных условиях, получает право и гарантированную возможность уделять преимущественное внимание тем направлениям, которые в наибольшей степени отвечают его склонностям.
В отечественной системе образования накоплен значительный опыт реализации дифференциации обучения математике: существуют и работают школы с углубленным изучением математики, специальные классы той же направленности, система факультативных занятий, кружков, элективных занятий, преподавание ведется по учебникам Ш.А. Алимова, М.И. Башмакова, Г.В. Дорофеева, Ю.М. Колягина, А.Г. Мордковича и др., в которых учебный материал излагается дифференцированно. В том числе авторы выделяют три уровня задачного материала: обязательные задачи, дополнительные более сложные задачи и трудные задачи. Однако, как показывает практика, на ранжирование задач по уровням никак не влияет структура решения этих задач и, соответственно, сложность решения.
Под дифференциацией при обучении математике мы понимаем способ организации вариативного учебного процесса, при котором учитываются индивидуальные особенности, присущие группам учеников. При этом уровневая дифференциация в обучении математике основывается на планировании результатов обучения: явном выделении уровня обязательной подготовки, задаваемого стандартом математического образования, и формировании на этой основе повышенных уровней овладения материалом [2]. Исходя из этих позиций, нами была построена технология дифференцированного обучения учащихся 7–9 классов решению текстовых задач алгебраическим способом.
Технология дифференцированного обучения учащихся 7–9 классов решению текстовых задач алгебраическим способом включает целевой (предметные цели овладения алгебраическим способом решения текстовых задач, усвоения приемов поиска пути решения текстовых задач, освоения способом применения моделирования при решении текстовых задач, развивающие цели), содержательный (цикл взаимосвязанных систем задач) и процессуальный (методы и средства обучения и учения) компоненты.
Концептуальные идеи авторской технологии дифференцированного обучения учащихся 7–9 классов решению текстовых задач алгебраическим способом: идеи теории задачного подхода в аспекте формирования операций способа или метода [1], основные положения концепций индивидуализации и дифференциации обучения о разноуровневости изложения теории и формирования умений, ключевые позиции теории поэтапного формирования умственных действий.
Содержательный компонент технологии дифференцированного обучения решению текстовых задач алгебраическим методом представлен циклом взаимосвязанных систем задач, удовлетворяющих следующим требованиям: система задач должна быть взаимосвязанной; единой для всех учащихся, с возможностью выбора индивидуальной последовательности задач; в одну систему должны попасть задачи, в процессе решения которых используется один и тот же набор базовых знаний и приемов; задачи в системах должны находиться в определенной логике следования друг за другом при постепенном нарастании сложности задач на базе их внутренней структуры; системообразующим элементом каждой системы задач должны являться конструкции графов определенных типов. Цикл образуется путем включения в него систем задач, каждая из которых сформирована из задач более сложной структуры.
При разработке технологии нами были с достаточной степенью условности выделены 5 уровней сложности структуры текстовых задач на процессы. В рамках статьи мы не демонстрируем типологию, а только обозначаем идею отбора задач для каждого уровня. Ниже представлены типичные примеры задач для каждого уровня.
1-й уровень – связи между величинами даны в явном виде, за х принимается та неизвестная величина, значение которой требуется найти.
Задача 1.1: Расстояние по реке между пунктами А и В равно 84 км. Из этих пунктов одновременно навстречу друг другу вышли две моторные лодки, собственные скорости которых различаются в 1,8 раза. Через 3 ч они встретились. Найдите собственные скорости лодок (задача на движение навстречу друг другу, рис. 1, а).
Задача 1.2: Из города А в город В, расстояние между которыми составляет 20 км, одновременно вышли 2 пешехода. Скорость одного из них была на 1 км/ч больше скорости другого, поэтому он затратил на весь путь на 60 мин меньше. Какова скорость каждого пешехода? (на движение в одном направлении, рис. 1, б).
Задача 1.3: Из Москвы в Санкт-Петербург выехал автобус. Спустя 1 ч вслед за ним вышла легковая машина, скорость которой на 20 км/ч больше скорости автобуса. Машина обогнала автобус и через 5 ч после своего выхода находилась впереди него на 70 км. Найдите скорость автобуса (на «обгон», рис. 1, в).
Задача 1.4: Из порта одновременно вышли два катера, один – на юг, другой – на север. Через 3 ч расстояние между ними составило 96 км. Найдите скорость первого катера, если она на 10 км/ч больше скорости второго катера (на движение в противоположных направлениях с началом пути в одной точке, рис. 1, г).
Задача 1.5: Из двух городов, находящихся на расстоянии 25 км друг от друга, в противоположных направлениях выехали два автомобиля. Через 2 часа после начала движения расстояние между ними увеличилось до 365 км. С какими скоростями двигались автомобили, если известно, что скорость одного на 10 км/ч больше другого? (на движение в противоположных направлениях с началом пути из разных точек, удаленных друг от друга на указанное в условии задачи расстояние, рис. 1, д).
2-й уровень – связи между величинами даны в явном виде, за х неудобно принять ту неизвестную величину, значение которой требуется найти. Например, требуется найти время или расстояние, а удобнее за x обозначить производительность или скорость.
Задача 2.1: Океанский лайнер отправился в рейс. Когда он отошел от берега на 180 миль, за ним вылетел самолет с экстренной почтой. Скорость самолета в 10 раз больше скорости лайнера. На каком расстоянии от берега самолет догонит лайнер?
Задача 2.2: Пешеход рассчитал, что, двигаясь с определенной скоростью, он пройдет намеченный путь за 2,5 ч. Но, увеличив скорость на 1 км/ч, он прошел это путь за 2 ч. Найдите длину пути.
3-й уровень – связи между величинами даны в неявном виде, за х принимается та неизвестная величина, значение которой требуется найти.
 а)
а)  б)
б)
 в)
в)  г)
г)
 д)
д)
Рис. 1. Схемы, иллюстрирующие структуры текстовых задач, отнесенных к 1-му уровню
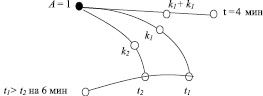
Рис. 2. Граф для задачи (*)
Задача 3.1: Каждый из рабочих должен был изготовить 36 одинаковых деталей. Первый рабочий приступил к выполнению своего задания на 4 мин позже второго, но 1/3 задания выполнили одновременно. Полностью выполнив свое задание, первый рабочий после двухминутного перерыва снова приступил к работе и к моменту выполнения задания вторым рабочим изготовил еще две детали. Сколько деталей в час изготавливал каждый рабочий?
4-й уровень – связи между величинами даны в неявном виде, за х неудобно принять ту неизвестную величину, значение которой требуется найти.
Задача 4.1: Две машинистки, работая вместе, печатают в час 44 страницы текста. Первые 25 % двухсотстраничной рукописи печатала первая машинистка, затем к ней присоединилась вторая, а последние 20 % текста печатала только вторая машинистка. Сколько страниц в час печатает каждая машинистка, если на перепечатывание всей рукописи ушло 6 ч 40 мин, а первая машинистка работает быстрее второй?
5-й уровень – в условии задачи описаны более двух процессов. Например:
Задача 5.1: Расстояние между двумя городами скорый поезд проходит на 4 ч быстрее товарного и на 1 ч быстрее пассажирского. Найдите скорости товарного и скорого поездов, если известно, что скорость товарного составляет 0,625 % от скорости пассажирского и на 50 км/ч меньше скорости скорого.
Задача 5.2: Три цистерны одинакового объема начинают одновременно заполняться водой, причем в первую цистерну поступает 100 л воды в минуту, во вторую – 60 л и в третью – 80 л. Известно, что в начальный момент времени первая цистерна пуста, вторая и третья частично заполнены и что все три цистерны будут заполнены одновременно. Во сколько раз количество воды в начальный момент времени во второй цистерне больше, чем в третьей?
Задача 5.3: Четыре одинаковых насоса, работая вместе, наполнили нефтью первый танкер и треть второго танкера (другого объема) за 11 ч. Если бы 3 насоса наполнили первый танкер, а затем один из них наполнил четверть второго танкера, то работа заняла бы 18 ч. За сколько часов 3 насоса могут наполнить второй танкер?
Задача 5.4: Три автоматические линии выпускают одинаковую продукцию, но имеют разную производительность. Производительность всех трех одновременно работающих линий в 1,5 раза выше производительности первой и второй линий, работающих одновременно. Сменное задание для первой линии вторая и третья линии, работая вместе, могут выполнить на 4 ч 48 мин быстрее, чем его выполняет первая линия; это же задание вторая линия выполняет на 2 ч быстрее по сравнению с первой линией. Найдите время выполнения первой линией своего сменного задания.
В рамках каждого уровня по сложности структуры текстовых задач на процессы были сконструированы системы разноуровневых задач. Разноуровневость в данной технологии выступает в двух аспектах: уровни сложности структуры текстовых задач на процессы и уровни трудности реализации решения задачи.
Источником систем задач выступают типовые задачи (так, например, для первого уровня их 5, см. выше), к которым подобраны аналогичные задачи, обеспечивающие тренинг и формирование системы базовых блоков знаний по способу решения текстовых задач. Далее для типовых задач осуществлено варьирование данных, приводящее к увеличению трудности решения (вычисление на другом множестве чисел, усложнение вычислительных преобразований, составление другого типа уравнений / неравенств и т.п.) и подбор аналогичных им задач для обеспечения тренинга. Также в систему задач обязательно включаются задачи с трансформациями условия и/или заключения (в том числе задачи с параметрами).
Индивидуализация и дифференциация обучения решению текстовых задач обеспечивается циклом взаимосвязанных систем задач, однако мы признаем возможность использования и отдельных систем задач в процессе обучения математике в основной школе.
Для реализации технологии дифференцированного обучения учащихся 7–9 классов решению текстовых задач алгебраическим способом разработана «система ориентиров», необходимая в случае, когда ученик не готов к самостоятельному решению или поиску пути решения текстовой задачи, которая включает в себя: теоретический материал (два уровня изложения: теория в виде «шпаргалки» и ориентировочная основа), чертеж к задаче (два уровня: чертеж-схема и чертеж с указанием всех данных в соответствии с условием задачи), указание к задаче (два уровня указаний: пошаговые указания и обобщенные рекомендации), динамические чертежи, модель в виде графа [3].
При работе с типовыми задачами (фронтально или в группах) формируется алгоритм поиска пути решения и хода решения задачи путем моделирования явных и неявных связей (основание – психологическая концепция Л.К. Максимова [4] по организации учебного моделирования).
Приведем систему вопросов по поиску пути решения задачи (*):
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
– О каких и скольких процессах ведется речь в задаче? (О работе, 2 процесса)
– Какими величинами характеризуется работа? (Производительность, время, работа)
– Как связаны между собой эти величины? (A = k·t)
– Какие из величин известны по условию задачи? (Время совместной работы – 4 мин; первая труба наполняет резервуар на 6 минут дольше, чем вторая)
– Каков основной вопрос задачи? (За сколько минут наполняет этот резервуар одна вторая труба?)
– Что в условии задачи сказано о работе? (Одинаковая)
– Изобразим на графе связи между величинами (рис. 2)
– Какую величину удобно обозначить за х?
Далее ведется работа по анализу связей между известными, принятыми за х величинами и найденными по арифметическим связям на ребрах графа.
Представленная технология прошла длительную апробацию в школах г. Волгограда и Волгоградской области. Результаты апробации свидетельствуют о устойчивой повторяемости положительных результатов.
Рецензенты:
Сергеев А.Н., д.п.н., профессор, заведующий кафедрой информатики и информатизации образования, ФГБОУ ВПО «Волгоградский государственный социально-педагогический университет», г. Волгоград;
Сахарчук Е.И., д.п.н., профессор кафедры педагогики, ФГБОУ ВПО «Волгоградский государственный социально-педагогический университет», г. Волгоград.
Работа поступила в редакцию 30.12.2014.
Библиографическая ссылка
Смыковская Т.К., Машевская Ю.А., Вихляева О.М. ТЕХНОЛОГИЯ ДИФФЕРЕНЦИРОВАННОГО ОБУЧЕНИЯ УЧАЩИХСЯ 7–9 КЛАССОВ РЕШЕНИЮ ТЕКСТОВЫХ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ // Фундаментальные исследования. – 2014. – № 12-11. – С. 2468-2472;URL: https://fundamental-research.ru/ru/article/view?id=36716 (дата обращения: 20.04.2024).



