Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Безуглов Д.А. 1 Решнтникова И.В. 2 Юхнов В.И. 3 Енгибарян И.А. 3

---

1 Ростовский филиал Российской таможенной академии

2 ФГБОУ ВПО «Ростовский государственный университет путей сообщения»

3 СКФ Московского технического университета связи и информатики

В рамках кумулянтного подхода к описанию статистических свойств пуассоновских сигналов и шумов проведен строгий анализ процесса фотодетектирования в датчике Гартмана. Получены аналитические выражения для характеристической функции и плотности распределения случайной величины, описывающей процессы, протекающие в системе. Вычислено отношение правдоподобия, а также получены оптимальные оценки величины локальных наклонов фазового фронта. Исследованы свойства полученных плотностей распределения. Следует подчеркнуть, что предложенный подход является оптимальным только в случае регистрации фотоприемниками слабых сигналов, когда смесь сигнала и шума хорошо аппроксимируется распределением Пуассона. В случае отличия плотности распределения смеси сигнала и шума от пуассоновского возможно получение аналогичных выражений для оптимальных оценок на базе предложенного подхода анализа кумулянтов соответствующих величин и процессов.

Статья в формате PDF

1923 KB

адаптивная оптическая система фазового сопряжения

датчик Гартмана

1. Безуглов Д.А. Фотодетектирование пуассоновских сигналов в лазерных дифференциальных доплеровских системах // Оптика и спектроскопия. 1996. – Т. 80, № 6. – С. 995–1000.

2. Безуглов Д.А. Кумулянтный метод оценки эффективности сегментированного зеркала адаптивной оптической системы // Оптика атмосферы и океана. – 1996. – № 1. – С. 78.

3. Безуглов Д.А. Оценка эффективности градиентного алгоритма стохастической аппроксимации в условиях воздействия шумов //Автоматика и вычислительная техника.  – 1996. – № 4. – С. 15–23.

4. Безуглов Д.А., Мищенко Е.Н., Мищенко С.Е. Адаптивные оптические системы. Методы восстановления фазового фронта // Оптика атмосферы и океана. – 1996. – Т. 9, № 3. – С. 44.

5. Безуглов Д.А., Сахаров И.А., Решетникова И.В. Метод оптимизации топологии датчика фазового фронта // Оптика атмосферы и океана. – 2008. – Т. 21, № 11. – С. 998–1003.

6. Безуглов Д.А., Сахаров И.А., Решетникова И.В. Оптимизации топологии датчика волнового фронта // Известия Южного федерального университета. Технические науки. – 2008. – № 3(80). – С.140–149.

7. Безуглов Д.А., Скляров А.В. Оценка точностных характеристик датчика Гартмана при регистрации пуассоновских сигналов // Измерительная техника. – 1999. – № 9. – С. 38.

8. Безуглов Д.А., Скляров А.В., Забродин Р.А., Решетникова И.В. Алгоритмы оценивания негауссовских процессов на основе математического аппарата сглаживающих В-сплайнов // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. – 2005. – № 4. – С. 99–106.

9. Безуглов Д.А., Скляров А.В., Забродин Р.А., Решетникова И.В. Субоптимальный алгоритм оценивания на основе аппарата сглаживающих В-сплайнов // Измерительная техника. – 2006. – № 10. – С. 14–17.

10. Безуглов Д.А., Цугурян Н.О. Дифференцирование результатов измерений сглаживающими кубическими В-сплайнами // Современные информационные технологии. – 2005. – № 1 (1). – С. 73–78.

11. Безуглов Д.А., Швидченко С.А. Информационная технология вейвлет-дифференцирования результатов измерений на фоне шума // Вестник компьютерных и информационных технологий. – 2011. – № 6 (84). – С . 42–45.

12. Калиенко И.В., Безуглов Д.А., Решетникова И.В. Численно-аналитический метод моделирования систем дифференциальных уравнений с периодическими коэффициентами // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. – 2006. – № 3. – С. 10–14.

Одним из основных элементов адаптивной оптической системы фазового сопряжения является датчик Гартмана. Проводя суммарно-разностную обработку сигналов с выхода квадрантных фотоприемников датчика, получают сигналы, пропорциональные локальным наклонам фазового фронта вида:

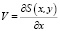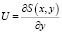, , (1)

где S(x, у) – распределение фазы на апертуре оптической системы.

В данной работе на базе математического аппарата кумулянтного анализа получены выражения для плотности распределения и характеристической функции исследуемых случайных величин. Получено выражение для оптимальной оценки величин U^ и V^ на фоне пуассоновских шумов [6, 7, 8, 9].

Пусть на квадрантный фотоприемник одного канала датчика Гартмана падает сфокусированный линзой световой поток малой интенсивности. При наличии наклона фазового фронта для вычисления его величины предполагается суммарно-разностная обработка сигналов:

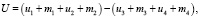
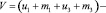
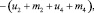(2)

где т_i – аддитивные пуассоновские шумы; и_i – полезный пуассоновский сигнал, соответствующий i-му квадранту фотоприемника.

С учетом того, что как т_i так и и_i являются пуассоновскими, в дальнейшем целесообразно рассмотреть выражение (2), представленное в виде

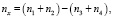
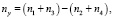(3)

где n_i = т_i + и_i – пуассоновская случайная величина. Примем следующие обозначения:

,

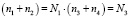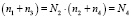, (4)

где N_i – пуассоновская случайная величина с параметром l.

При этом было учтено, что при отсутствии локального наклона на субапертуре гартмановского датчика интенсивность оптического поля на всех квадрантах фотоприемника одного канала будет равна [1, 2, 3, 4, 5]. Математические ожидания величин nx и ny будут равны:

,

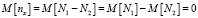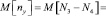
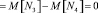, (5)

где М – символ математического ожидания.

Начальные моменты после несложных преобразований с учетом соотношения (5) запишутся в следующем виде:

,

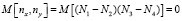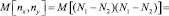
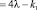, (6)

где k₁ – коэффициент корреляции случайных величин N_i .

Учитывая природу пуассоновских шумов, коэффициент корреляции необходимо положить равным 0. При дальнейшем рассмотрении нижний индекс случайных величин nx, ny опустим и будем рассматривать случайную величину n.

Моменты случайной величины n порядка k запишутся в следующем виде:

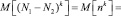
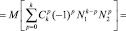
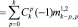, (7)

где 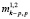– совместные моменты случайных величин N₁ и N₂ порядка k–p, p.

Здесь и в дальнейшем при обозначении порядка моментов и кумулянтов случайных величин нижние индексы будут соответствовать их порядку, а верхние обозначать соответствующую случайную величину.

Из (7) видно, что все нечетные моменты 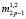случайной величины п равны нулю. Значения совместных моментов случайных величин N₁ и N₂ 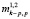, входящие в состав выражения (7), для четных 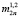не могут быть определены в общем случае как нулевые.

В случае независимости двух случайных величин N₁ и N₂ все их совместные кумулянты будут равны нулю, чего нельзя сказать однозначно о соответствующих совместных моментах. Именно такой случай имеется в рассматриваемой физической задаче. В силу того что регистрация потока фотоэлектронов осуществляется различными фотоприемниками, величины N₁ и N₂ можно считать независимыми. Поэтому в дальнейшем целесообразно перейти к рассмотрению системы кумулянтов случайной величины n. Они могут быть найдены на основе свойства линейности и инвариантности [3] из выражения (7):

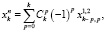
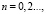(8)

где 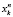– кумулянты порядка k случайной величины n, 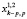– совместные кумулянты случайных величин N₁ и N₂.

Основываясь на вышеизложенном относительно значений совместных кумулянтов, нетрудно прийти к выводу, что случайная величина n описывается системой только четных кумулянтов:

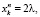
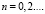(9)

Запишем выражение для характеристической функции искомого распределения плотности вероятности:

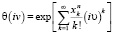. (10)

С учетом (9) выражение (10) запишется в следующем виде:

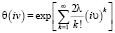. (11)

Суммируя ряд в квадратных скобках, получим

θ(iv) = exp[2λ(ch(iυ) – 1] =

= exp[2λ(cos(υ) – 1]. (12)

Для получений аналитического выражения плотности распределения преобразуем по Фурье характеристическую функцию (12):

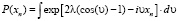. (13)

С учетом известного выражения для разложения показательной функции в ряд

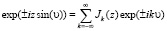, (14)

где J_k(z) – функция Бесселя k-го порядка, после несложных преобразований получим

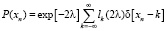, (15)

где l_n(2λ) – модифицированные функции Бесселя k-го порядка, δ – дельта-функция.

Так как случайная величина n принимает только дискретные значения ± n, окончательное выражение для искомой плотности запишется в следующем виде:

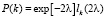. (16)

Легко видеть, что полученная плотность (16) нормирована с весом 1. Просуммировав выражение (16) по всем индексам k, получим

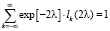. (17)

Очевидно, что в случае наличия наклона фазового фронта кружок Эйри на квадрантном фотоприемнике будет смещен, при этом параметры пуассоновских распределений, соответствующих случайным величинам N₁ и N₂, не равны

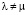, (18)

где λ – параметр распределения случайной величины N₁, μ – параметр распределения случайной величины N₂. В этом случае

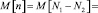
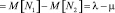. (19)

Для системы кумулянтов случайной величины n в общем случае будет верно выражение (8). Все совместные кумулянты в силу независимости оптических сигналов в каналах датчика Гартмана равны нулю. Нечетные кумулянты x_2k–1 равны λ – μ, четные кумулянты x_2n равны λ + μ. Это связано с тем, что (– 1)^k при четных k и выражении (8) дает только положительные члены, а при нечетных k – знакочередующиеся. С учетом этого характеристическая функция такого распределения запишется в следующем виде:

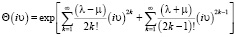. (20)

С учетом разложения функций cos u и sin u в степенной ряд запишем

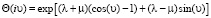. (21)

Используя известные соотношения для функций Бесселя [4], будем иметь

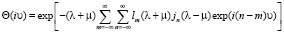. (22)

Для нахождения аналитического выражения для плотности распределения случайной величины п преобразуем по Фурье полученную характеристическую функцию (22):

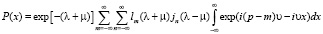. (23)

В результате интегрирования этого выражения получим

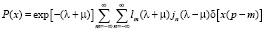. (24)

Для фиксированных значений случайной величины n, а именно этот случай нас интересует в конечном итоге, исходя из физической постановки задачи при p – m = k, имеем

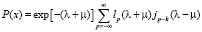. (25)

Для получения оптимальной оценки величины λ – μ необходимо вычислить логарифм отношения правдоподобия. Для этого преобразуем полученную плотность (25) в соответствии с теоремой умножения функций Бесселя:

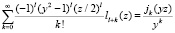. (26)

Положим, y = i(λ/μ)^0,5, z = 2μ, тогда

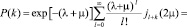
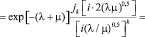
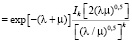. (27)

Для определения отношения-правдоподобия разобьем интервал регистрации сигнала на выходе датчика Гартмана t на ряд элементарных подинтервалов длительностью t_i, i = 1,…r. Процесс появления фотоэлектронов на отдельных подинтервалах является статистически независимым. Совместное распределение на всем интервале τ можно представить в виде произведения соответствующих одномерных плотностей распределения. Многомерную плотность распределения запишем в следующем виде [10, 11, 12]:

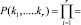
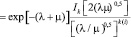. (28)

Оптимальную оценку λ + μ получим из решения уравнения вида

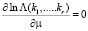, (29)

где

.

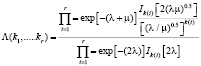При λ, μ < 0 функции Бесселя можно представить в виде:

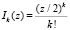. (30)

Тогда, подставив (28), (30) в выражение (29), после несложных преобразований получим

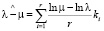, (31)

где k_i – отсчеты фотоэлектронов в i-й момент времени на выходе датчика Гартмана.

Вместо λ и μ можно использовать их оценки. Так как λ и μ по определению являются пуассоновскими величинами, то их оценки могут быть получены известными методами.

Выводы

В результате проделанных аналитических выкладок получено выражение (31) для оптимальной в статистическом смысле оценки сигналов на выходе датчика Гартмана адаптивной оптической системы фазового сопряжения. Плотность распределения сигнала на выходе датчика Гартмана в случае отсутствия наклона фазового фронта является симметричной и унимодальной. Однако при этом она существенно отличается от гауссовой вследствие неравенства нулю высших кумулянтов. При регистрации в обоих каналах сигналов различной интенсивности плотность распределения остается унимодальной, однако смещается по оси абсцисс, и оптимальная оценка сигнала на выходе системы должна находиться в виде (31).

Рецензенты:

Звездина М.Ю., д.ф.-м.н., доцент, заведующая кафедрой «Радиоэлектроника», Минобрнауки России, ФГБОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону;

Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС», г. Ростов-на-Дону.

Работа поступила в редакцию 15.04.2015.

Библиографическая ссылка