Известно, что любой вычислительный эксперимент, вместе с критериями истинности, должен характеризоваться рядом специальных параметров, связанных с особенностями математической адаптации, моделирования и используемого численного алгоритма. В данной работе описывается постановка вычислительного эксперимента по нахождению установившихся параметров электродинамической системы дифракции электромагнитных волн (ЭМВ), рассеивателем в которой является однородный слабопроводящий цилиндр, обладающий не нулевой угловой скоростью вокруг своей оси. Представление результатов эксперимента не является целью этого текста, в нем показывается нахождение некоторых качественных параметров компьютерной модели, необходимых для корректного симулирования.
Эксперимент оценивается по трем параметрам: чувствительность, стабильность и вариативность. Чувствительность определяет, на какое минимальное значение могут быть изменены входные величины, чтобы проследить требуемое изменение в выходных данных при требуемой точности. Стабильность системы показывает диапазон входных и выходных параметров, при котором соблюдаются корректные вычисления всех величин, входящих в модель. Вариативность описывает возможности анализируемой модели вне диапазона стабильности и вводится, в первую очередь, для того, чтобы проследить путь развития и усовершенствования эксперимента.
Математическая модель
Основы физической системы и ее геометрия описаны в [1]. Отправным математическим аппаратом являлись решения уравнения Максвелла при заданных граничных условиях, полученные в [3], с помощью методов, описанных в [5], и развернутые на типовые вращающиеся системы в [2]. Используемые решения для амплитуд представляются в виде рядов сумм, вычисляемых в интересующей нас точке пространства системы (r, φ, z) (PoI).
Для проекции амплитуды напряженности электрического поля падающей волны, на ось перпендикулярную волновому вектору (z)
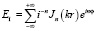 . (1)
. (1)
Для проекции амплитуды напряженности электрического поля рассеянной волны на ось z
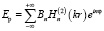 . (2)
. (2)
Для проекции амплитуды напряженности электрического поля волны внутри цилиндра на ось z
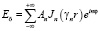 . (3)
. (3)
Реализация компьютерной модели, ко всему прочему, требует программной адаптации представленных выше формул. Естественно ряды дискретизируются, и первым шагом к определению чувствительности эксперимента является нахождение допустимой величины приближения бесконечности, при которой ряды сходятся и дают результат с необходимой степенью точности. На рис. 1 представлены диаграммы рассеяния (ДР) цилиндра при одинаковых входных физических параметрах, но при разных n (слева). Справа графически показана функция разности (Dn = f1(φ)–f2(φ)) значений амплитуды поля при n = 10 и n = 100 от углов, на которых строились ДР. М – медиана разности. Среднеквадратичное отклонение – 0,035 (амплитуда облучения нормируется по единице).
Результаты для n = 100 полностью соответствуют ожидаемым значениям, таким образом, статистические величины указывают на определенное отклонение от заданной точности, при вычислении рядов для n = 10. Дальнейшая вариация значения n показала, что для частоты падающей волны до 1ГГц разность значений для n = 60 и n = 100 строго равна нулю. Выше этой частоты выбор значения n во многом зависит от характера проводимого эксперимента.
В силу того что подавляющее большинство экспериментов с моделью проходило на частоте в указанном выше диапазоне, ниже будут даваться результаты работы модели при n = 60. Стоит отметить, что среднеквадратичное отклонение разности значений при n = 20 и n = 100 составляет всего 0,000027. При соблюдении этой степени точности, в целях экономии времени симулирования, в некоторых экспериментах имеет смысл вычислять ряды в таком приближении бесконечности. Очевидно, что n → ∞, однако при этом и t → ∞, где t – время проведения эксперимента. Для оценки временных ресурсов можно применить к анализу т.н. итерационный множитель «x», который показывает, сколько производится дополнительных итераций внутри основного цикла вычислений ряда за один шаг. Минимально возможное значение для эксперимента x = 13 (зависит от требуемых выходных параметров). При n = 100 общее количество итераций в цикле расчета ряда для одной координаты системы – nx = 1300. При получении ДР в дальней зоне излучения цилиндра заданным количеством точек аппроксимируется окружность PoI. Для представленных в этой работе рисунков количество точек в окружности – 401; общее количество итераций в эксперименте – 521300. Подобный эксперимент, только с другим рассеивателем, ставился в [4]. Для большей экономии времени эксперименты проводились при n = 10. Из рис. 1 видно, что качественный ход ДР можно получить и при этих значениях – это оправдано в тех случаях, когда точность представления результатов, не сопоставима с точностью самих результатов.
Для более детальной оценки чувствительности выражение для амплитуды падающей волны может быть переписано с использованием ряда Лорана (как и выражения для рассеянной и прошедшей волны) следующим образом:
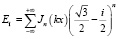 . (4)
. (4)
Вычисление по формуле (4) также дает точный результат при n = 60 (в указанном диапазоне частот). Однако, начиная с частоты падающей волны 3ГГц, в результате вычисления ряда появляется мнимая составляющая порядка 10-10, которая должна отсутствовать. При увеличении n до 100, она исчезает. На частоте в 10ГГц появляется погрешность в реальной части результата порядка 0,001, которая исчезает с увеличением n до 120. Подобные погрешности в представленных выше формулах отсутствуют. Дальнейшее увеличение частоты нецелесообразно, потому что при более высоких частотах модель становится не стабильной по ряду других параметров. Уменьшение частоты вплоть до 1МГц на точность вычисления этого ряда не сказывается.
Вычислительные алгоритмы
Анализ системы происходит в частотной области, поэтому цилиндр выбирается круглым и однородным, чтобы не наблюдать модуляцию отраженной волны с течением времени. Все пространство системы разбивается на координаты, независимо от их местоположения (внутри цилиндра или снаружи), они могут являться PoI, в которых происходит расчет амплитуды и фазы электромагнитного поля. Точность в задании координат указывает дискретность контуров, по которым производятся вычисления. В случае построения круговых диаграмм точность PoI является точностью аппроксимации окружности, лежащей в дальней зоне излучения цилиндра. Расчет также производится и на поверхности рассеивателя. Единственным ограничением является невозможность установить значения поля в начале координатной сетки, величина приближения к ней выбирается произвольно. Разумный предел точности для PoI – 1 ангстрем. Для оценки параметров эксперимента, имеет смысл использовать т.н. коэффициенты соотносимости:
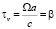 ,
, 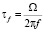 ,
, 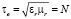 ,
,
τ = τv + τf + τe. (5)
Все эти коэффициенты безразмерны и призваны установить корреляцию входных и выходных параметров модели. В них: Ω – угловая скорость вращения цилиндра, a – радиус цилиндра, f – частота падающей волны, εrμr – относительная диэлектрическая и магнитная проницаемость цилиндра. Также для оценки чувствительности использовался показатель среды σ/ωε0 и близкий к нему по смыслу τ/σ, где σ – проводимость цилиндра. Эксперимент стабилен в случае, когда цилиндр является неидеальным диэлектриком.
Из математической записи видно, что β ≤ 1. На рис. 2 показана ДР цилиндра при разных значениях β, а также их функция разности.


Рис. 1. Сравнение результатов при различных длительностях рядов


Рис. 2. Результаты для различных скоростей вращения цилиндра (τf = 7,96∙10-4 для β = 0,05 и τf = 0,16 для β = 1)


Рис. 3. Сравнение результатов для различных τ/σ(σ/ωε0 = 1,8 для τ/σ = 20,05 и σ/ωε0 = 0,018 для τ/σ = 2005; N = 2)
Модель ведет себя стабильно при τf ≤ 1. При условии a ≈ λ, и при максимальной скорости вращения цилиндра – τf ≈ 1/2π, что является оптимальным значением для данного коэффициента. При прочих скоростях вращения цилиндра соотносимость значений уменьшается и зависит от отношения Vл/c, где Vл – линейная скорость вращения цилиндра. При низких скоростях чувствительность эксперимента относительно неподвижного рассеивателя стремится к нулю, при прочих равных условиях.
На рис. 3 представлены ДР и функция разности, при различных значениях τ/σ.
При увеличении проводимости выше σ = 3 См/м эксперимент перестает быть стабильным, полученные результаты расходятся с ожидаемыми по ряду параметров. Фактически, чем выше значение τ/σ, тем стабильнее проявляет себя эксперимент.
Наряду с ДР показательным результатом обработки экспериментальных данных является ЭПР цилиндра. При многочисленных экспериментах удалось установить, что, зная ЭПР (Q) цилиндра, возможно аппроксимировать его ДР, с помощью ДН плоского прямоугольного резонатора.
Установлены примерные соотношения геометрических размеров эквивалентного неподвижному цилиндру резонатора, в диапазоне стабильности эксперимента: а (ширина) = 0,84λ; b(длина) = Q\a. Для неподвижного цилиндра ряд значений ДР и ДН эквивалентного резонатора примерно одинаковы (при заданной точности): Δθ-3дБ ≈ 30 °(ширина диаграммы по уровню половины мощности), δ ≈ – 18дБ (уровень боковых лепестков). Вращение цилиндра несущественно изменяет эти значения (в зависимости от коэффициентов соотносимости). В случае качественного несовпадения ДР цилиндра с ДН эквивалентного резонатора, можно говорить о нестабильности в работе симулятора.
Заключение
Вариативность модели устанавливается из анализа стабильности эксперимента, частичный анализ которого был представлен в этом тексте. Эксперимент может быть использован в широком диапазоне входных значений, при различных вариациях точности, времени получения и представления результатов. Модель имеет большой потенциал к усовершенствованию, что может предоставить возможность для постановки новых экспериментов.
Исследование выполнено за счет гранта Российского научного фонда (проект № 14-19-01396).
Данная работа получила награду «Лучший доклад» по итогам конференции «Информационные технологии, телекоммуникации и системы управления», УрФУ, ИРИТ-РтФ, 15 декабря 2014 года.
Рецензенты:
Шабунин С.Н., д.т.н., профессор кафедры высокочастотных средств радиосвязи и телевидения, ФГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург;
Иванов В.Э., д.т.н., профессор, заведующий кафедрой ТСС ИРИТ-РтФ, ФГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Работа поступила в редакцию 15.04.2015.
Библиографическая ссылка
Зейде К.М. АНАЛИЗ ПАРАМЕТРОВ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА ПО РАССЕЯНИЮ ЭМВ ОТ ВРАЩАЮЩЕГОСЯ ЦИЛИНДРА // Фундаментальные исследования. – 2015. – № 2-16. – С. 3503-3507;URL: https://fundamental-research.ru/ru/article/view?id=37808 (дата обращения: 23.04.2024).



