Целью настоящей статьи является восстановление сосредоточенных масс и коэффициентов жесткости пружин, сосредоточенных на тупиковых вершинах звездного струнного графа, по известному набору собственных частот колебаний этого графа. Дифференциальные операторы на графах часто возникают в естествознании и технике [11]. Прямые спектральные задачи решались в работах [6, 8, 15], так же решались обратные спектральные задачи (см., например, [9, 12, 14]), в том числе на графах [13]. Однако существенным отличием этих работ от данной является то, что коэффициенты дифференциальных уравнений и краевых условий восстанавливаются не по части спектра, а по нескольким спектрам и (или) по некоторым другим спектральным характеристикам. К тому же основной целью этих работ является восстановление коэффициентов в уравнении, а не в краевых условиях. Идентификации краевых условий спектральных задач по собственным значениям в механических и электронных системах посвящена работа [3], однако рассмотренная нами задача там не изучалась. В [5] восстанавливались коэффициенты граничных условий оператора Штурма – Лиувилля по всему спектру (а не по конечному набору собственных частот). Близкая задача рассматривалась в работе [10], но для электрических систем. Это задача идентификации условий заземления через последовательно сосредоточенные самоиндукцию и емкости конденсатора. Восстанавливаются 6 параметров краевых условий по 6 собственным значениям, однако в этом случае получаются лишние решения, которых не будет, если известно большее число собственных значений задачи. В работах [1, 2, 3] восстанавливались только сосредоточенные массы или только жесткости пружинок на концах струнного графа, а не все параметры одновременно.
В данной работе рассматривается задача идентификации сосредоточенных масс и коэффициентов жесткости пружин, сосредоточенных на тупиковых вершинах звездного струнного графа по известному набору собственных частот. Из-за общности уравнений для электрических колебаний в проводе [4, 7] и механических колебаний струны результаты, представленные в данной работе для механической системы, справедливы и для подобной электрической системы. Для электрической сети сосредоточенным массам на концах струнного графа соответствуют индуктивности, а обратные величины коэффициентов упругости (жесткостей) пружин, закрепляющего концы графа, соответствуют емкостям.
Результаты, полученные в данной работе, позволяют получать механические системы с заданным спектром колебаний, проектировать виброзащитные системы, сохраняющие приборы от ударного воздействия, проводить диагностику таких систем, а также диагностировать условия заземления электрических сетей на участках, труднодоступных для визуального осмотра.
Постановка обратной задачи. Рассмотрим граф G в виде звезды из n ребер-струн с одним общим концом в нуле. Длина i-й струны равна li. Тупиковые концы струн упруго закреплены, причем каждая из струн может быть закреплена пружинками неодинаковой жесткости hi. В местах упругого закрепления подвешены-сосредоточены массы mi. Требуется определить сосредоточенные массы mi и коэффициенты жесткости пружин hi струнного графа по собственным частотам колебаний графа. Ниже для наглядности изложения этот метод решения приводится для случая n = 3.
Спектральная задача для каждого ребра колеблющегося графа имеет вид
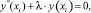 0 ≤ xi ≤ li, i = 1, 2, 3, (1)
0 ≤ xi ≤ li, i = 1, 2, 3, (1)
где xi – расстояние от общего узла по оси OXi; y(xi) – вертикальные смещения c выходом из плоскости начального расположения струнного графа, а 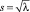 – спектральный параметр.
– спектральный параметр.
Точка O (xi = 0) является свободной (подвижной). Условия в точке О имеют вид [3]
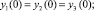 (2)
(2)
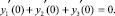 (3)
(3)
Краевые условия на тупиковых вершинах таковы:
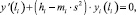 i = 1, 2, 3. (4)
i = 1, 2, 3. (4)
Формулы (2) выражают условия непрерывности, а (3) – баланс сил, действующих на общую вершину графа (точку О – узел) со стороны каждого из примыкающих к узлу ребер, условия (4) – условия упругого закрепления ребер (струн) с сосредоточенными массами.
Математически в терминах введенных обозначений сформулируем постановку задачи.
Постановка задачи: Пусть li = 1 (i = 1, 2, 3). Требуется найти hi и mi по известному набору собственных значений sk задачи (1)–(4).
Метод введения дополнительных неизвестных. Перед решением этой обратной задачи напомним, как решается прямая задача нахождения собственных значений.
Решением уравнения (1) является следующая функция:
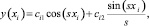 (5)
(5)
где ci1 и ci2 – произвольные константы. Подставляя функции (5) в (2)–(4) соответственно, получим, что собственные значения sk задачи (1)–(4) находятся из частотного уравнения
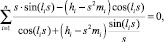
i = 1, 2, 3. (6)
Изложим теперь метод решения обратной задачи. Система уравнений (6) при s = sk (k = 1, 2, ...,) является нелинейной относительно неизвестных hi (i = 1, 2, 3) и mi (i = 1, 2, 3). И если для определения 6 неизвестных hi и mi использовать также 6 собственных значений, то, как правило, помимо диагностируемых данных окажутся и другие лишние решения. Система может иметь 6! = 720 наборов решений, из которых достаточно трудоемко исключить лишние решения. Но при решении вышеуказанной задачи машина зависает при расчете, поскольку нужно выдать 720 вариантов наборов 6 параметров. Поэтому для решения этой задачи предложен следующий численный метод – метод введения дополнительных неизвестных. С помощью введения дополнительных неизвестных приведем уравнение (6) к линейному виду:
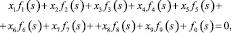 (7)
(7)
где 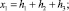
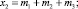
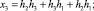
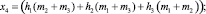
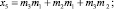
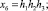

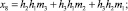
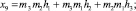 (8)
(8)
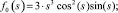
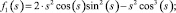
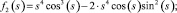
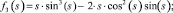
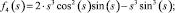
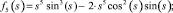
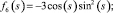
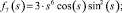
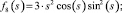
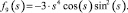 (9)
(9)
Функции f0(s), f1(s), f2(s), f3(s), f4(s), f5(s), f6(s), f7(s), f8(s), f9(s) являются линейно независимыми функциями аргумента s (по определению линейной независимости функций).
Пусть s1, s2, s3, s4, s5, s6, s7, s8, s9 – собственные значения задачи (1)–(4) подставим их в (7). В результате получим систему девяти линейных уравнений от девяти неизвестных {x1, x2, x3, x4, x5, x6, x7, x8, x9}:
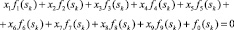 , k = 1, 2, 3, 4, 5, 6, 7, 8, 9. (10)
, k = 1, 2, 3, 4, 5, 6, 7, 8, 9. (10)
Из правил Крамера следует, что если определитель матрицы
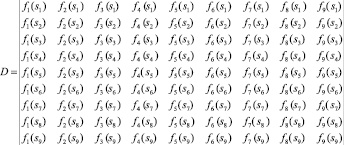 (11)
(11)
системы уравнений (10) отличен от нуля, то неизвестные {x1, x2, x3, x4, x5, x6, x7, x8, x9} находятся единственным образом по формулам 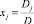 (j = 1, 2, ..., 9), где Dj – определитель матрицы, получаемый заменой j-го столбца столбцом свободных членов.
(j = 1, 2, ..., 9), где Dj – определитель матрицы, получаемый заменой j-го столбца столбцом свободных членов.
Справедлива следующая теорема.
Теорема 1. Если s1, s2, ..., s9 являются точными собственными значениями краевой задачи (1)–(4), D ≠ 0, то система (10) имеет единственное решение {x1, x2, x3, x4, x5, x6, x7, x8, x9}, определяемое по формулам Крамера 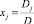 (j = 1, 2, ..., 9), а значения коэффициентов жесткости пружинок h1, h2, h3 и сосредоточенных масс m1, m2, m3 находятся с точностью до перестановок закреплений на тупиковых концах механической системы местами по формулам (8).
(j = 1, 2, ..., 9), а значения коэффициентов жесткости пружинок h1, h2, h3 и сосредоточенных масс m1, m2, m3 находятся с точностью до перестановок закреплений на тупиковых концах механической системы местами по формулам (8).
Пример. Пусть
s1 = 0.5351947856; s2 = 0.7209194738;
s3 = 1.7077687399; s4 = 3.2007784617;
s5 = 4.7562882600; s6 = 6.312233015;
s7 = 7.8802149625; s8 = 9.4440741650;
s9 = 11.0142910657
являются собственными значениями краевой задачи L и длины струн l1 = l2 = l3 = 1. Требуется найти h1, h2, h3, m1, m2, m3.
Решая систему линейных уравнений (7), получим
x1 = 6.00012454515180; x2 = 11.0002292716576; x3 = 6.00012584636183;
x4 = 15.0002729440572; x5 = 74.0013465243788; x6 = 120.002183553839;
x7 = 58.0011800634226; x8 = 51.0010534591865; x9 = 138.002713340072.
Подставляя {x1, x2, x3, x4, x5, x6, x7, x8, x9} в (8), получим 36 наборов решений, из которых только 6 наборов являются искомыми:
1. {h1 = 3.00027942412555, h2 = 1.00001056019994, h3 = 1.99983456082631,
m1 = 6.00196131492730, m2 = 4.00058303446869, m3 = 4.99772859466121};
2. {h1 = 1.99983456082631, h2 = 1.00001056019994, h3 = 3.00027942412555,
m1 = 4.99772859466121, m2 = 4.00058303446869, m3 = 6.00196131492730};
3. {h1 = 3.00027942412555, h2 = 1.99983456082631, h3 = 1.00001056019994,
m1 = 6.00196131492730, m2 = 4.99772859466121, m3 = 4.00058303446869};
4. {h1 = 1.00001056019994, h2 = 1.99983456082631, h3 = 3.00027942412555,
m1 = 4.00058303446869, m2 = 4.99772859466121, m3 = 6.00196131492730};
5. {h1 = 1.99983456082631, h2 = 3.00027942412555, h3 = 1.00001056019994,
m1 = 4.99772859466121, m2 = 6.00196131492730, m3 = 4.00058303446869};
6. {h1 = 1.00001056019994, h2 = 3.00027942412555, h3 = 1.99983456082631,
m1 = 4.00058303446869, m2 = 6.00196131492730, m3 = 4.99772859466121}.
Итак, закрепления на тупиковых концах механической системы мы можем восстановить с точностью до перестановок их местами по 9 собственным значениям, используя новый метод – метод введения дополнительных неизвестных. В то время как если рассматривать граф из трех струн и восстанавливать одновременно и сосредоточенные массы и коэффициенты жесткости пружинок (6 параметров) на концах струнного графа по 6 собственным значениям, то получим 6! или 720 наборов решений, из которых достаточно трудоемко исключить лишние решения. И при решении задачи машина зависает при расчете, поскольку нужно выдать 720 вариантов наборов 6 параметров.
Рецензенты:
Спивак С.И., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования, ФГБОУ ВПО «Башкирский государственный университет», г. Уфа;
Султанаев Я.Т., д.ф.-м.н., профессор, главный научный сотрудник лаборатории «Механика твердого тела», ФГБУН «Институт механики им. Р.Р. Мавлютова» Уфимского научного центра Российской академии наук, г. Уфа.
Библиографическая ссылка
Ахтямов А.М., Ахтямов А.М., Аксенова З.Ф. О ДИАГНОСТИКЕ МЕХАНИЧЕСКОЙ СИСТЕМЫ ИЗ СТРУН ПО КОНЕЧНОМУ НАБОРУ СОБСТВЕННЫХ ЗНАЧЕНИЙ // Фундаментальные исследования. – 2015. – № 5-1. – С. 27-31;URL: https://fundamental-research.ru/ru/article/view?id=38002 (дата обращения: 20.04.2024).



