Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гоц А.Н. 1

---

1 ФГБОУ ВПО «Владимирский государственный университет им. Александра Григорьевича и Николая Григорьевича Столетовых»

При расчете деталей машин методом конечных элементов возникает затруднение в выборе детерминированной модели при определении коэффициентов запаса прочности. Во всех программных комплексах, где используется метод конечных элементов, в качестве детерминированной модели при известном тензоре напряжений в окрестностях некоторой узловой точки для определения амплитудных и средних напряжений используется интенсивность напряжений, определяемая при максимальном и минимальном нагружении. Однако при этом не учитывается тот факт, что площадки, где интенсивность напряжений определяется при действии максимальной и минимальной нагрузок, будут разными, а значит, расчет получается не вполне корректным. Если же определить интенсивность амплитуд переменных напряжений, вычисленных в одних и тех же площадках, а в качестве среднего напряжения выбрать наибольшее постоянное напряжение цикла, то результаты расчетов запасов прочности будут отличаться от расчетов по интенсивности напряжений.

Статья в формате PDF

512 KB

тензор напряжений

детерминированная модель

амплитудные напряжения

средние напряжения

интенсивность напряжений

запас прочности

1. Белов Е.С. Расчет составного блок-картера одноцилиндрового дизеля / Е.С. Белов, Б.Ю. Голев, А.Н. Гоц и др. // Фундаментальные и прикладные проблемы совершенствования поршневых двигателей: Материалы XII Междун. научно-практ. конференции; под ред. А.Н. Гоца. – Владимир: ВлГУ, 2010. – С. 114–118.

2. Гоц А. Н. Расчет щеки коленчатого вала ДВС / А.Н. Гоц, И.Н. Куделя // Тракторы и сельскохозяйственные машины. – 1998. – № 9. – С. 26–31.

3. Гоц А.Н. Детерминированные модели усталостной долговечности деталей ДВС / Тракторы и сельскохозяйственные машины. – 1997. – № 12. – C. 19–21.

4. Гоц А.Н. Расчеты на прочность деталей ДВС при напряжениях, переменных во времени.– 3-е изд., исп. и доп. – М.: ФОРУМ: инфра-м, 2013. – 208 с.

5. Гоц А. Н. Выбор детерминированной модели усталостной долговечности / А.Н. Гоц, А.Б. Иванченко // Актуальные проблемы управления качеством производства и эксплуатации транспортных средств: материалы IX междунар. науч.-практ. конф. / Владим. гос. ун-т. – Владимир: ВлГУ, 2002. – С. 311–314.

6. Гоц А.Н. Выбор детерминированной модели усталостной долговечности при расчете деталей поршневых двигателей на переменные нагрузки // Сб. научных трудов Международной конференции Двигатель-2010, посвященной 180-летию МГТУ им. Н.Э. Баумана / под ред. Н.А. Иващенко, В.А. Вагнера, Л.В. Грехова. – М.: МГТУ им. Н.Э. Баумана, 2010. – С. 44–49.

7. Гоц А.Н. Расчеты на прочность деталей ДВС при напряжениях, переменных во времени: учеб. пособие. – 2-е изд., испр. и доп.; Владим. гос. ун-т, – Владимир: Изд-во Владим. гос. ун-та, 2011. – 140 с.

8. Гоц А.Н. Определение запаса прочности щеки коленчатого вала с положительным перекрытием / А.Н. Гоц, И.Н. Куделя // Двигателестроение. – 1999. – № 4. – С. 15–18.

9. Детерминированные и статистические модели долговечности / И.А. Биргер // Проблемы прочности летательных аппаратов: сб. ст.; под ред. И.Ф. Образцова, А.С. Вольмира. – М.: Машиностроение, 1985. – 280 с.

10. Пономарев С.Д. Расчеты на прочность в машиностроении / С.Д. Пономарев [и др.]. В 3 т. Т. 3 / под ред. С.Д. Пономарева. – М.: Машгиз, 1959. – 1118 с.

При расчете деталей поршневых двигателей методом конечных элементов (МКЭ) возникает вопрос о выборе детерминированных моделей усталостной долговечности. Как правило, при использовании наиболее распространенных программных комплексов расчета МКЭ в качестве гипотезы разрушения при сложном напряженном состоянии используется гипотеза удельной энергии формоизменения (гипотеза Губера – Мизеса – Генки), в которой эквивалентное напряжение определяется через интенсивность напряжений (или октаэдрическое касательное напряжение) по формуле [4]

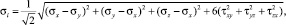(1)

или через главные напряжения

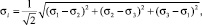(1, а)

где σ_x, σ_y, σ_z, τ_xy, τ_yz, τ_zx – компоненты тензора напряжений в окрестности узловой точки конечно-элементной модели:

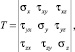(2)

σ₁, σ₂ и σ₃ – главные напряжения, определяемые при том же тензоре напряжений.

Известно [10], что результаты с использованием этой гипотезы достаточно хорошо согласуются с экспериментальными данными не только в области упругих деформаций, но и в пластической области в случае статического нагружения. Это дало повод использовать интенсивность напряжений при определении запасов прочности или долговечности деталей ДВС в случае нагружения их переменной нагрузкой. Другими словами, при переменном действии нагрузок для расчета интенсивности напряжений σi по формуле (1) в качестве исходного выбирают сначала максимальное нагружение, а затем минимальное, что позволяет найти σ_imax, а затем σ_imin, а далее оперировать ими, как обычно, как максимальными и минимальными напряжениями. Однако полученные при этом σ_imax и σ_imin получены для разных площадок, так как главные площадки могут быть во взаимно перпендикулярных площадках. Это было отмечено нами ранее в случае расчета даже для плоского напряженного состояния [4].

При действии сначала максимальных, а затем и минимальных нагрузок компоненты тензора напряжений (2) в окрестностях каждой точки конечно-элементной модели будут иметь разные значения. Значит, будут разными для каждого вида нагружения главные напряжения и положения площадок, в которых они действуют. Действительно, если при статическом нагружении определяется эквивалентное напряжение для какой-то определенной площадки, положение которой нас даже не интересует, то при использовании (1) в случае переменных нагрузок напряжения σ_imax и σ_imin будут определены для площадок, никак не связанных между собой (в некоторых случаях они могут быть взаимно перпендикулярными). Это значит, что запасы прочности при переменных напряжениях или запасы долговечности будут вычисляться, мягко говоря, не вполне корректно, поскольку амплитудные и средние напряжения определены с использованием напряжений, вычисление которых проводилось по формуле (1,а) в разных площадках.

Если графически интерпретировать прогнозирование разрушения по гипотезе удельной энергии формоизменения, то поверхность разрушения представляет круговой цилиндр, ось которого образует равные углы с тремя главными осями (рис. 1). Эти круговые цилиндры при разных видах нагружения могут пересекать друг друга, так как соотношение главных напряжений (и положение взаимно перпендикулярных площадок) σ₁ > σ₂ > σ₃ будет различным при максимальной и минимальной нагрузке. Круговые цилиндры располагались бы по типу «матрешки» и стороны их были бы эквидистантными, если бы циклы переменных напряжений при максимальной и минимальной нагрузках были бы подобными (с одинаковыми коэффициентами асимметрии). Естественно, что вероятность такого нагружения весьма мала.

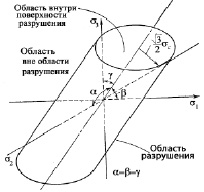
Рис. 1. Графическое представление гипотезы удельной энергии формоизменения для случая произвольного напряженного состояния

И.А. Биргером была предложена детерминированная модель усталостной долговечности, применимая при расчете любых конструкций в условиях переменного нагружения [9] и проверенная нами при расчетном исследовании широкого круга деталей ДВС [1–8]. Для расчета эквивалентного амплитудного напряжения σ_ea при сложном напряженном состоянии (при объемном тензоре напряжений в случае расчета МКЭ) и действии переменных нагрузок предложены зависимости:

эквивалентное напряжение

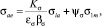(3)

где K_σ – эффективный коэффициент концентрации напряжений; ε_σk – масштабный коэффициент (влияния абсолютных размеров детали); β_σ – коэффициент поверхностной чувствительности; ψ_σ – коэффициент, учитывающий влияние средних напряжений на предел выносливости 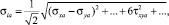[4];

(4)

σ_ia – интенсивность амплитуд переменных напряжений цикла σ_xa, σ_ya, ..., τ_xya, τ_yza, ... (вычисленных по известному тензору напряжений [10]); σ_1m – наибольшее постоянное напряжение цикла (первое главное напряжение.

Заметим, что поскольку расчет МКЭ велся при максимальном и минимальном нагружении для одних и тех же площадок, то противоречие в расчетах, отмеченное нами ранее, в данном случае пропадает. Кроме того, в зависимости (3) используется наибольшее постоянное напряжение цикла (первое главное напряжение), как раз учитывающее то обстоятельство, что определяемые главные напряжения при переменном нагружении будут в разных площадках.

Проведем сравнение расчетных данных с использованием (1) и (3) на примере расчета запасов прочности составного блок-картера одноцилиндрового дизеля [1]. На рис. 2 показана расчетная конечно-элементная модель блок-картера, которая состояла из 247028 элементов и 457782 узлов [4, 9]. Для расчета использовался программный комплекс Ansys 11.0¹ Наибольшие напряжения возникали в сечениях вокруг бобышки (см. рис. 2 – показаны стрелками), которая является коренной опорой. Максимальная нагрузка на блок-картер возникала при действии газовой силы и сил инерции деталей, совершающих возвратно-поступательное движение, а минимальная – только от действия сил инерции на режиме максимальной частоты вращения холостого хода [1].

В табл. 1 и 2 приведены значения компонентов тензоров напряжений в окрестности некоторых точек блок-картера при действии максимальной нагрузки (газовой и сил инерции, табл. 1) и минимальной (только сил инерции, табл. 2).

В последних столбцах табл. 1 и 2 приведены значения эквивалентных напряжений, вычисленных по формуле (1), а на рис. 3 показаны точки конечно-элементной модели, где эквивалентные напряжения σ_i в соответствии с гипотезой потенциальной энергии формоизменения достигают максимального значения.

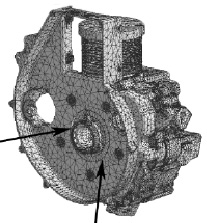
Рис. 2. Расчетная КЭ модель сборки блок-картера: узлов – 457782, элементов – 247028

Как следует из табл. 2, при действии только сил инерции численные значения компонентов тензоров напряжений в тех же узловых точках, а также эквивалентные напряжения уменьшаются.

Таблица 1

Компоненты тензоров напряжений при действии газовых и инерционных сил

Таблица 2

Компоненты тензоров напряжений при действии сил инерции

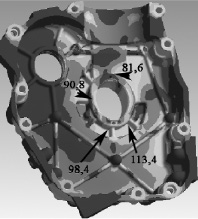
Рис. 3. Значения эквивалентных напряжений

Все программные комплексы для расчета деталей ДВС методом МКЭ приводят в результате расчета значения интенсивности напряжений σ_i, которые и представляют собой значение эквивалентных напряжений, вычисленное по формуле (1). На рис. 3 приведена конечно-элементная модель блок-картера, а стрелками показаны эквивалентные напряжения при действии газовых и инерционных сил. В этих точках в эксплуатационных условиях появлялись трещины.

Мы уже отмечали, что эти напряжения являются эквивалентными в случае статического нагружения, но их использовать для расчета запасов прочности или долговечности при действии переменных напряжений (при максимальной нагрузке – как максимальные, а минимальной – минимальные) не вполне корректно, а кроме того, приводит к неверным результатам.

Для использования модели (3) проведем расчет амплитудных нормальных и касательных напряжений в соответствии с данными табл. 1 и 2. После этого определим амплитудные значения нормальных, касательных, а также интенсивность амплитуд напряжений переменных циклов в соответствии с зависимостью (3). Запасы прочности определим по зависимости [4]:

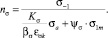(5)

Здесь σ_–1 – предел выносливости при изгибе при симметричном цикле. Смысл значений K_σ, β_σ, Ψ_σ, σ_1m приведен выше.

Расчеты проводились при следующих исходных данных: K _σ = 1,4; ε_σk = 0,9; β_σ = 0,9; Ψσ = 0,2 [27];σ_–1 = 120 МПа. Результаты расчетов приведены в табл. 10. Расчеты проводились с учетом того, что сначала определялись эквивалентные амплитудные напряжения, а второй расчет, когда амплитудные и средние напряжения определялись с учетом зависимости.

Анализируя полученные результаты (табл. 3), замечаем, что расчет с учетом эквивалентных амплитудных напряжений по зависимости (3) дает значения запасов прочности значительно ниже, чем расчет по эквивалентным напряжениям (формула (1)). Полученные результаты расчетного исследования НДС блок-картера и экспериментальная проверка полученных результатов показала, что выявленные зоны с пониженными коэффициентами запаса прочности действительно имели место. После внесения изменений в конструкцию блок-картера прочность была обеспечена.

Таблица 3

Амплитудные значения нормальных, касательных и амплитуды эквивалентных напряжений, а также запасы прочности

Таким образом, для расчета на действия переменных напряжений необходимо внести в известные расчетные комплексы дополнительно расчет амплитудных межцикловых напряжений и амплитудного эквивалентного напряжения в соответствии с детерминированной моделью И.А. Биргера.

Рецензенты:

Кобзев А.А., д.т.н., профессор, ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир;

Кульчицкий А.Р., д.т.н., профессор, главный специалист ООО «Завод инновационных технологий» КТЗ, г. Владимир.

[1] Расчеты проводились Б.Ю. Голевым и Е.С. Беловым.

Библиографическая ссылка