Одной из задач, часто решаемых при обработке изображений трехмерного объекта, является оценка параметров их поворота. При известной нумерации отсчетов, например в системах астроориентации, где предварительно производится идентификация звезд в кадре, оценка параметров может быть выполнена матричным методом [2]. В ситуациях, когда на наблюдаемое изображение воздействуют различные помеховые факторы, неизвестна нумерация отсчетов исходного и наблюдаемого объекта, не совпадает их количество, наблюдаемый объект представлен фрагментом, определение параметров поворота матричным методом становится невозможным. В работах [4–7] рассмотрены методы обработки изображений трехмерного объекта с известной и неизвестной нумерацией отсчетов, обеспечивающие возможность оценки параметров поворота изображений трехмерного объекта, однако при этом необходима информация обо всей поверхности объекта. Решение указанной задачи возможно на базе корреляционных алгоритмов, однако они обладают высокой трудоемкостью в условиях априорной неопределенности относительно параметров поворота, масштабирования и переноса, что затрудняет их реализацию в реальном или близком к нему масштабе времени.
В данной работе предлагается решение указанной проблемы на базе преобразования Хафа. В работе [3] рассмотрено модифицированное обобщённое преобразование Хафа, обеспечивающее возможность распознавания изображений трехмерных объектов по их фрагментам при произвольном масштабе и неизвестных параметрах поворота. Однако этот метод не позволяет получить оценки параметров поворота изображения трехмерного объекта.
Целью данной работы является разработка алгоритма оценки параметров вращения изображения пространственного объекта на базе преобразования Хафа, в том числе по их фрагментам.
Определение параметров поворота изображения трехмерного объекта
Как показано в [1], определение параметроаповорота отсчетов трехмерного объекта может быть описано с помощью тензора поворота:
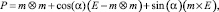 (1)
(1)
где P – тензор поворота; ⊗ – знак тензорного произведения; m⊗m – тензор второго порядка; m – ось вращения; α – угол поворота вокруг оси; E – единичный тензор.
Сам поворот описывается следующим выражением:
v′ = Pv, (2)
где v′ – вращаемый вектор; v – исходный вектор.
Тогда вращаемый вектор определяется как
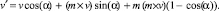 (3)
(3)
На основании (3) составим выражения для определения координат вращаемого вектора:
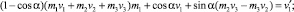
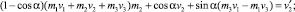 (4)
(4)
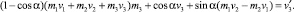
Решая систему (4) относительно m1, m2, m3 получим два решения. Первое решение:
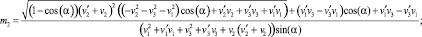
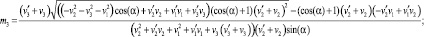
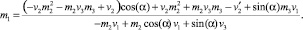
Второе решение:
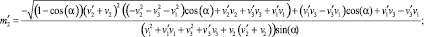
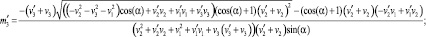
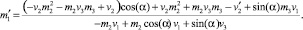
Для оценки параметров поворота воспользуемся подходами, заложенными в классическом преобразовании Хафа. При определении параметров поворота пространственного объекта [4–7] исходными данными являются координаты точек эталонного и обрабатываемого изображений. На их базе могут быть рассчитаны векторы нормалей к поверхности объекта, которые вращаются аналогично объекту и нечувствительны к преобразованиям переноса, масштабирования. Методика расчета полей нормали объекта представлена в [3]. При определении параметров поворота необходимо оценить четыре неизвестных параметра: три параметра – координаты оси вращения и четвертый угол поворота. Согласно выражениям свободным параметром преобразования Хафа будет угол вращения. Исходными данными для определения параметров поворота трехмерного объекта будут координаты векторов нормалей к поверхности эталонного и повернутого объектов.
Для свободного параметра необходимо задать пределы его изменения. На рис. 1 показаны возможные направления векторов оси вращения m1 и m2, рассчитываемые на основе данных о направлениях нормалей исходного объекта v, отсчетов нормалей повернутого объекта v′ и угла поворота α. Для однозначного выбора направления оси вращения диапазон изменения угла α задается в пределах от 0 до 180°.
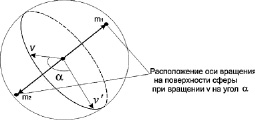
Рис. 1. Расположение оси вращения
Поскольку каждый вектор нормали отсчета исходного объекта сравнивается с каждым вектором нормали вращаемого объекта, рассматриваемый вариант преобразования Хафа не чувствителен к нумерации отсчетов. При расчете координат осей вращения для очередного вектора нормали исходного объекта и вектора нормали вращаемого объекта находят координаты оси вращения при некотором угле α. Поскольку угол α принимает все допустимые значения, то в результате определяются координаты возможных при данных условиях осей вращения, пересечение которых в аккумуляторном массиве создаст пик.
В ряде случае решения системы не существуют или не удовлетворяют условию нормировки оси вращения m. При этом голосование не проводится и считается, что поворот с такими параметрами невозможен.
Поскольку неизвестными являются четыре параметра поворота, то и аккумуляторный массив должен быть четырехмерным, что затрудняет реализацию данного метода. Однако, поскольку вектор оси вращения является нормированным, то для его представления достаточно знания двух его компонент, а третья может быть вычислена с точностью до знака. В связи с этим предложено использовать трехмерный аккумуляторный массив A[my, mz, α], содержащий координаты оси вращения по осям y, z и значение угла поворота.
После выделения пика в аккумуляторном массиве определяются его индексы. Поскольку знание координат пика в аккумуляторном массиве не позволяет непосредственно находить знак третьей компоненты вектора оси вращения, необходимо повторно провести расчеты координат осей вращения, и если получаемые при этом индексы совпадают с найденными ранее, то рассчитанные значения координат оси вращения и угла поворота принимают в качестве результатов оценки параметров поворота трехмерного объекта.
С учетом изложенного алгоритм оценки параметров вращения на базе преобразования Хафа будет включать следующие этапы
1. Расчет векторов нормали исходного и вращаемого объекта.
2. Для данного вектора нормали отсчета исходного объекта – v.
3. Для данного вектора нормали отсчета вращаемого объекта – v′.
4. Для некоторого угла вращения α векторов нормали отсчета исходного объекта и вращаемого объекта.
5. Расчет в соответствии с (5), (6) координат оси вращения.
6. Если ось вращения существует и ее длина равна единице, то инкрементируется элемент аккумуляторного массива A[my, mz, α].
7. Нахождение индексов пика в аккумуляторном массиве .
8. Повтор пунктов 1–6 и поиск соответствия индексов оси вращения индексам пика в аккумуляторном массиве, нахождение координаты оси вращения mx.
9. Конец.
Одним из достоинств преобразования Хафа является возможность оценивать свойства структуры по его фрагменту. Алгоритм обработки изображения в этом случае аналогичен алгоритму, но вращаемый объект может задаваться отдельным фрагментом.
Экспериментальная оценка помехоустойчивости разработанного алгоритма, определения параметров вращения пространственного объекта на базе преобразования Хафа
Для определения помехоустойчивости разработанного метода оценки параметров поворота изображений трехмерных объектов была проведена серия вычислительных экспериментов в соответствии со следующим алгоритмом.
1. Формируются отсчеты исходного объекта и отсчеты вращаемого объекта, получаемые поворотом исходного объекта с параметрами вращения {mx, my, mz, α}.
2. Производится зашумление отсчетов вращаемого объекта аддитивным нормальным шумом с нулевым математическим ожиданием и дисперсией
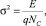
где 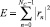 – энергия сигнала; rn – расстояние каждого отсчета до центра формы; Nc – количество отсчетов на изображении; q – отношение сигнал/шум:
– энергия сигнала; rn – расстояние каждого отсчета до центра формы; Nc – количество отсчетов на изображении; q – отношение сигнал/шум:
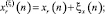
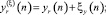
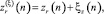
где 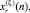
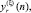
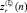 – зашумленные отсчеты повернутого объекта.
– зашумленные отсчеты повернутого объекта.
3. Выполняется расчет полей нормалей объектов.
4. В соответствии с алгоритмом выполняется оценка параметров поворота изображений трехмерного объекта.
5. Пп. 2–4 повторяются Nоп раз, в каждом опыте оцениваются параметры поворота и затем для каждой координаты оси вращения и угла поворота вычисляется среднеквадратичное отклонение вычисленных параметров поворота трехмерного объекта относительно истинных значений параметров {mx, my, mz, α}.
6. Серии опытов по определению параметров вращения объекта повторяются для различных значений отношения сигнал/шум. По их результатам строится график зависимости среднеквадратического отклонения каждого из оцениваемых параметров поворота изображений трехмерного объекта от отношения сигнал/шум.
На рис. 2 представлены изображения тестовых объектов, участвовавших в эксперименте, объект и его фрагмент. Модель получена из базы данных эталонного теста Princeton Shape Benchmark [8]. При определении параметров поворота изображений трехмерного объект использовался аккумуляторный массив A[my, mz, α] размерностью 500×500×180. На рис. 3–6 приведены результаты экспериментов, погрешности оценки каждого параметра вращения при использовании алгоритма, для модели объекта (рис. 2 а) и его фрагмента (рис. 2 б).


а б
Рис. 2. Модели объекта и его фрагмента, используемые в эксперименте: а – целый объект; б – фрагмент объекта
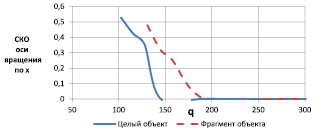
Рис. 3. Характеристика оценивания координаты х оси вращения
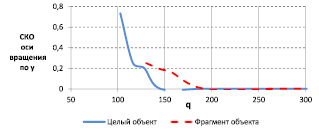
Рис. 4. Характеристика оценивания координаты y оси вращения
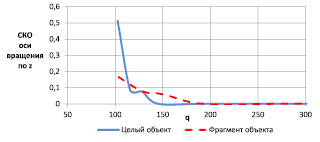
Рис. 5. Характеристика оценивания координаты z оси вращения
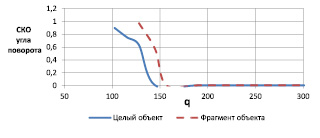
Рис. 6. Характеристика оценивания угла поворота
Как видно из полученных результатов, параметры поворота полного изображения объекта оцениваются с удовлетворительным качеством при отношениях сигнал/шум q < 140, а при оценке параметров фрагмента изображения объекта требуемое отношение сигнал/шум увеличивается до 170.
Заключение
В работе рассмотрен подход к оценке параметров поворота изображений трехмерного объекта, базирующийся на преобразовании Хафа. Его основным достоинством является возможность работы с трехмерными объектами независимо от ракурса наблюдения в случаях, когда их отсчеты неупорядочены или в кадре находится только фрагмент объекта. Предложенные алгоритмы имеют относительно низкую трудоемкость O(n3) по сравнению с пространственно-корреляционными методами.
Рецензенты:
Хафизов Р.Г., д.т.н., профессор кафедры РТиМБС, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола;
Рябов И.В., д.т.н., профессор кафедры ПиП ЭВС, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.
Библиографическая ссылка
Морозовский К.В. ОЦЕНКА ПАРАМЕТРОВ ПОВОРОТА ИЗОБРАЖЕНИЯ ПРОСТРАНСТВЕННОГО ОБЪЕКТА НА БАЗЕ ПРЕОБРАЗОВАНИЯ ХАФА // Фундаментальные исследования. – 2015. – № 9-3. – С. 491-496;URL: https://fundamental-research.ru/ru/article/view?id=39211 (дата обращения: 25.04.2024).



