Известные подходы к моделированию потребления электроэнергии в жилых домах в общем случае можно разделить на две большие группы: «нисходящие» (top-down) и «восходящие» (bottom-up). Подобная терминология объясняется характером входных данных, а именно степенью их детализации, позицией в иерархии относительно множества жилых строений, для которого производится моделирование.
Оценку величины расходуемой электроэнергии при помощи нисходящих моделей применяют с целью определения взаимосвязей между этой величиной и параметрами, характеризующими объект исследования (регион или целую страну). В таких моделях как правило учитываются макроэкономические показатели.
Восходящие модели решают задачу оценки количества потребляемой энергии в отдельных домах, многоквартирных домах (МКД) или группах зданий с целью экстраполяции результата на регион или страну. В рамках этой группы дополнительно выделяют статистические (statistical methods, SM) и инженерные методы (engineering methods, EM). Статистические методы основываются прежде всего на использовании исторических данных и применении регрессионного анализа с целью выявления взаимосвязей между величинами потребляемой электроэнергии для отдельных пользователей и жилого строения в общем.
Инженерные методы полагаются на характеристики здания и некоторые данные о конечном пользователе, не требуя при этом для своей работы никаких исторических сведений (для построения модели исторические сведения тем не менее могут быть использованы) [13].
Главным преимуществом восходящих моделей перед нисходящими, очевидно, является возможность получения значений для объектов любых масштабов: от отдельных квартир до целых городов. В этом же заключаются и важнейшие недостатки такого подхода: более строгие требования, предъявляемые к данным, а также значительное усложнение вычислительных задач, решаемых при построении моделей.
Согласно описанным выше принципам классификации, модель, представленную в данной работе, можно отнести к восходящим моделям инженерного типа (bottom-up engineering model).
На протяжении нескольких десятилетий разработки в области таких моделей ведутся учеными из западных стран. В табл. 1 приведена сравнительная характеристика трех наиболее заслуживающих внимание, по мнению автора, моделей, разработанных в различных странах в разное время.
Таблица 1
Сравнение моделей, представленных в исследованиях [7, 9, 11]
|
Публикация |
Страна |
Количество записей |
Значение R2 (для частных домов) |
Значение R2 (для МКД) |
|
[7] |
Канада |
3640 |
0,37 (природный газ) 0,79 (доступно только электричество) |
– |
|
[9] |
США |
1628 |
0,48 («зимняя») 0,52 («летняя») |
– |
|
[11] |
Франция |
36955 |
0,35 |
0,34 |
Для количественной оценки и сравнения способности моделей «предсказывать» величину потребленной электроэнергии требуется определить специальный показатель, в качестве которого выбран коэффициент детерминации (R2). Коэффициент детерминации может быть определен следующим образом:
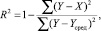
где Y – фактические значения зависимой переменной; Yсред – среднее значение по фактическим данным; X – модельные значения, построенные (восстановленные) по оцененным параметрам.
Среди отечественных исследований подобные модели, к сожалению, не представлены должным образом. В то же время следует отметить, что результаты исследований, упомянутых выше, по мнению автора, не могут считаться применимыми к российским реалиям. На это существует целый ряд причин различной степени очевидности.
Заметной особенностью описанных выше исследований является то, что все они в большей степени акцентируют свое внимание на отдельных домовладениях, т.е. частных домах, принадлежащих, как правило, одной семье. Это вполне соответствует реалиям развитых западных стран: Канады, Франции, США, – но в то же время не совсем подходит для России. Следует отметить климатические различия, а также разницу в менталитете, культуре и привычках потребителей из разных стран. Кроме того, заметное влияние могут оказывать принципы устройства системы коммунального хозяйства, доступность различных видов энергии (например, природного газа в России и Франции), макроэкономические факторы и т.д. Все это, по мнению автора, делает целесообразным изучение характерных особенностей российского потребителя энергоресурсов в целом и электроэнергии в частности на основе специально созданных моделей.
Модели потребления электроэнергии во многом определяются данными, на основе которых они строятся. Предложенный в данной статье подход описывает модель, обученную с применением данных из следующих источников
1. Сведения о потреблении электроэнергии, собранные при помощи системы АСКУПЭ, функционирующей на территории г. Саранска. Значения величины расхода детализированы до 1 дня и охватывают временной интервал 470 дней.
2. Информация биллинговой системы ООО «Саранский расчетный центр»: данные о конструктивных особенностях МКД, квартирах, их площадях и установленном оборудовании, а также сведения о жильцах.
3. Данные о внешней среде: продолжительность светового дня и температура воздуха, представленные в виде ежедневных значений в упомянутом выше временном интервале.
В основе подхода, описанного в данной статье, лежит метод опорных векторов. Метод опорных векторов (также известный как Машина опорных векторов, или SVM) – широко известная методология обучения по прецедентам, предложенная в 1995 году В.Н. Вапником [3]. Исследователи отмечают, что способность обобщения метода SVM делает его более эффективным по устойчивости модели, чем у искусственных нейронных сетей и нечеткой логики. Время сходимости алгоритма регрессии SVM при краткосрочном прогнозировании меньше, чем у искусственных нейронных сетей, алгоритм имеет более высокую точность прогнозирования, меньшее количество регулируемых параметров [1].
Пусть имеется обучающая выборка {(x1, y1), …, (x1, y1)} ⊂ χ×R, где χ определяет пространство входных значений. Задача ε-SV – регрессии состоит в нахождении функции f(x), которая:
1) не считает за ошибки отклонения от yi, меньшие некоторого значения ε для всей обучающей выборки;
2) при этом является наименее чувствительной к различного рода искажениям и ошибкам, имеющим место во входных данных (flatness) [12].
Для простейших случаев, когда f(x) является линейной функцией, мы можем сформулировать проблему в следующем виде:
f(x) = ⟨w, x⟩ + b, (1)
где w ∈ χ, b ∈ R; здесь ⟨.,.⟩ означает скалярное произведение в пространстве χ.
Выполнение условия (1) прежде всего подразумевает минимизацию значения
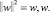
Минимизация в данном случае эквивалентна задаче квадратичного программирования с ограничениями типа неравенств:
минимизировать
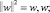
при условии
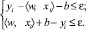 (2)
(2)
Формулируя задачу (2), мы делаем предположение о существовании некоторой функции f, аппроксимирующей все пары значений (xi, yi) с точностью ε. Иными словами, мы полагаем, что задача (2) разрешима. Однако в некоторых случаях это может быть не так. Кроме того, мы можем ослабить наши ограничения и допустить наличие некоторого количества ошибочных значений. По аналогии с «алгоритмом с мягким зазором» (soft-margin-SVM) мы можем ввести дополнительные переменные εi и 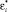 для решения подобных задач. Соответственно, формулировка задачи оптимизации примет вид:
для решения подобных задач. Соответственно, формулировка задачи оптимизации примет вид:
минимизировать
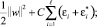
при условии
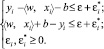
Константа C определяет баланс между чувствительностью функции f к ошибкам и верхним пределом, при котором отклонения, большие чем ε, считаются приемлемыми.
В некоторых случаях более естественным представляется использование кусочно-линейной функции ε-чувствительности [12]:

По аналогии с задачей классификации, при работе с SVM-регрессией используются так называемые ядра (kernel functions).
Функция K∶X×X → R называется ядром (kernel function), если она представима в виде 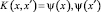 при некотором отображении ψ:X → H, где H – пространство со скалярным произведением [2].
при некотором отображении ψ:X → H, где H – пространство со скалярным произведением [2].
Использование ядер является одним из способов сделать регрессионную модель, основанную на построении линейной разделяющей поверхности, нелинейной [12]. Основная суть этого способа заключается в переходе от исходного пространства X к новому пространству H с более высокой размерностью с помощью некоторого преобразования ψ:X → H [2].
Метод опорных векторов позволяет добиться хороших результатов при решении самых разнообразных задач. Один из известных подходов к работе с SVM предполагает следующую последовательность действий [8]:
1. Преобразовать исходные данные в формат используемой SVM-библиотеки.
2. Применить масштабирование.
3. Использовать радиально-базисное ядро
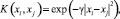 γ > 0.
γ > 0.
4. Использовать перекрестную проверку для нахождения лучших параметров C и γ.
5. Протестировать получившуюся модель.
Самая широко известная программная реализация алгоритма SVM представлена в виде библиотеки с открытым исходным кодом libsvm, разработанной в Национальном университете Тайваня. Существует большое количество программных интерфейсов, позволяющих относительно легко использовать libsvm совместно с различными языками и платформами. В данном исследовании для моделирования был использован язык R, который, будучи изначально спроектированным в качестве инструмента статистического анализа, предоставляет широкие возможности для работы с данными.
Архитектура системы анализа данных о потреблении электроэнергии, построенной в рамках исследования, определяется прежде всего источниками данных. Основные сведения, описывающие величину потребленной в жилых помещениях электроэнергии, поступают из АСКУПЭ в виде «плоских» файлов с разделителем. При помощи ETL-процесса эти сведения загружаются в базу данных биллинга, работающую под управлением Microsoft SQL Server 2008. Специально разработанный набор хранимых процедур предоставляет интерфейс для доступа к нужной информации со стороны R-кода. Данные о погоде и продолжительности светового дня, использованные при создании описываемой модели, получены при помощи специальных R-пакетов: weatherData и maptools.
Сведения, извлеченные из базы, в соответствии с описанным выше алгоритмом, нуждаются в предварительной обработке. Прежде всего, чтобы расcчитать потребленный за некоторый временной промежуток объем электроэнергии L, мы должны найти разность двух показаний:
L = V – V′,
где V и V′ – показания прибора учета на конец и начало временного промежутка соответственно.
Кроме того, данные, полученные из АСКУПЭ, нуждаются в очистке [4]. С целью выявления ошибочных данных во временных рядах может быть использована иерархическая кластеризация [10].
В качестве критерия подобия временных рядов выбрано евклидово расстояние, являющееся геометрическим расстоянием в многомерном пространстве [6]:
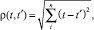
где t и t′ – некоторые временные ряды.
На основании матрицы подобия, содержащей значения евклидового расстояния для всех возможных пар временных рядов с помощью встроенной функции hclust производится кластеризация. Наиболее подходящим для нас будет результат, при котором все «нетипичные» временные ряды попадут в одни кластеры, а корректные, «типичные» – в другие. Для этого рекомендуется устанавливать количество кластеров равное [10]
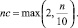
В результате процедуры очистки группы, содержащие «нетипичные» временные ряды, должны быть отброшены.
Еще одной проблемой, с которой исследователи неизбежно сталкиваются при работе с «реальными» источниками данных, является наличие пропущенных значений. Для языка R разработан многофункциональный пакет timeSeries, который среди большого множества инструментов анализа временных рядов предлагает разработчикам несколько подходов к решению проблемы отсутствующих данных. При создании описываемой в данной статье модели использовалась функция interpNA, содержащаяся в вышеупомянутом пакете и позволяющая восполнить пропущенные значения при помощи линейной интерполяции.
Согласно [8], точность SVM можно увеличить, если к имеющимся данным применить операцию масштабирования. Рекомендуется применять линейное масштабирование, в результате которого значения каждого из атрибутов будут лежать в диапазоне [–1, +1] или же [0, 1] (в данном исследовании использован второй вариант).
Категориальные атрибуты представлены в виде векторов вещественных чисел, причем для представления атрибута с m категориями используются m чисел. Например, переменная, описывающая тип стен многоквартирного дома и принимающая значения из множества {‘кирпичные’, ‘деревянные’, ‘бетонные’}, может быть представлена в виде трех векторов {0,0,1}, {0,1,0}, {1,0,0}.
Результирующий набор данных содержит порядка 6000000 суточных значений. Данные представлены следующими регрессорами: Площадь дома, Этаж, Площадь квартиры, Количество проживающих, Средний возраст проживающих, Время суток, Дата постройки, Среднесуточная температура, Продолжительность светового дня, Тип кровли, Тип фундамента, Тип отопления, Тип стен.
Таблица 2
Значения коэффициента детерминации для построенных моделей
|
№ п/п |
Использованные регрессоры |
МКД с электрическими плитами (R2) |
МКД с газовыми плитами (R2) |
|
1. |
Полный набор регрессоров |
0,724 |
0,390 |
|
2. |
(1) за исключением «Тип крыши» |
0,720 |
0,377 |
|
3. |
(1) за исключением «Средний возраст проживающих» |
0,684 |
0,330 |
|
4. |
(1) за исключением «Дата постройки здания» |
0,692 |
0,367 |
|
5. |
(1) за исключением «Среднесуточная температура», «Продолжительность светового дня» |
0,707 |
0,382 |
|
6. |
(1) за исключением «Площадь дома», «Площадь квартиры» |
0,691 |
0,367 |
|
7. |
(1) за исключением «Количество проживающих» |
0,712 |
0,383 |
Процедура обучения модели на основе машины опорных векторов в рамках данного исследования включает в себя следующие этапы:
а) Извлечение случайной выборки из набора имеющихся значений.
Имеющийся массив данных достаточно велик, и время, которое потребуется для обучения машины опорных векторов на его основе, может измеряться сутками.
б) Разбиение данных на 2 части: обучающий (2/3 от изначального количества записей) и тестовый (1/3 от изначального количества записей) наборы.
в) Подбор наиболее оптимальных значений C и γ на основе обучающего набора данных.
г) Оценка результативности модели на основе тестового набора данных.
Подбор параметров (или, точнее, гиперпараметров) C и γ для RBF-ядра может быть осуществлен с помощью специальной техники сеточного поиска (grid search) [5].
Большая часть многоквартирных домов в г. Саранске в соответствии со своими конструктивными особенностями подразумевают использование жильцами для приготовления пищи газовых плит. Проживающие в остальных домах используют с той же целью электроплиты. По аналогии с моделью, описанной в [7], все данные изначально были разделены по принципу доступности ресурсов в МКД на две группы: квартиры, оборудованные газовыми плитами, и квартиры, оборудованные электроплитами. Значения R2, рассчитанные для моделей при сравнении с результатами, представленными в табл. 1, позволяют говорить о приемлемом качестве разработанных моделей. Следует отметить, что количественная оценка влияния каждого из факторов на зависимую величину при использовании радиально-базисного ядра не представляется возможной. Однако, исследуя модели, построенные на основе различных наборов регрессоров, можно определить тот из них, который обеспечивает наилучшее соответствие модели данным. Согласно данным из табл. 2, наилучшие значения коэффициента детерминации достигнуты при использовании всех признаков.
Рецензенты:
Косников Ю.Н., д.т.н., профессор, заведующий кафедрой «Информационно-вычислительные системы», Пензенский государственный университет, г. Пенза;
Смогунов В.В., д.т.н., профессор, заведующий кафедрой теоретической и прикладной механики и графики, Пензенский государственный университет, г. Пенза.
Библиографическая ссылка
Федосин А.С. РЕГРЕССИОННАЯ МОДЕЛЬ ПОТРЕБЛЕНИЯ ЭЛЕКТРОЭНЕРГИИ ВОСХОДЯЩЕГО ТИПА // Фундаментальные исследования. – 2015. – № 9-3. – С. 522-527;URL: https://fundamental-research.ru/ru/article/view?id=39217 (дата обращения: 18.04.2024).



