Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гурбан И.А. 1 Тарасьев А.А. 1, 2

---

1 ФГБУН «Институт экономики Уральского отделения Российской академии наук»

2 Институт государственного управления и предпринимательства Уральский федеральный университет им. первого Президента России Б.Н. Ельцина

Статья посвящена задаче определения уровня инвестиций в сферу науки на уровне, необходимом для обеспечения устойчивого развития экономических систем. За минувшее десятилетие в России произошло сокращение численности персонала, занятого в научных отраслях. При этом произошло увеличение инвестиционных потоков в наукоемкие отрасли. Для корректировки и повышения отдачи от инвестиционных потоков необходимы научно обоснованные прогнозы, отражающие изменение динамики инвестиций в зависимости от результативности их использования. Для решения данной проблемы рассматривается модель пропорционального экономического роста, в которой динамика трудовых ресурсов удовлетворяет заданным условиям пропорциональности. Пропорциональность экономического развития в этой модели достигается за счет решения задачи оптимизации объема выпуска при заданных затратах на протяжении всего периода развития системы. Инвестиции в трудовые ресурсы в рамках модели выступают в роли управляющих параметров и предназначены для поддержания пропорционального развития экономических систем. Механизм ценообразования описан комбинацией модели дуополии Курно и степенной функции Кобба ‒ Дугласа. В рамках исследования задано соотношение пропорциональности между капиталом и трудовыми ресурсами, объединяющее их через механизм ценообразования по заработной плате на рынке труда. В соответствии с предлагаемой конструкцией пропорциональные решения агрегируются в общие затраты на трудовые ресурсы и передаются на верхний уровень оптимизации. Модель представлена в виде системы нелинейных дифференциальных уравнений, стационарные точки которой генерируют равновесные состояния экономики. В результате разработки данной модели возможно получение прогноза уровня общих инвестиций в трудовые ресурсы, необходимого для устойчивого развития рынка труда, на конечном и бесконечном горизонте.

Статья в формате PDF

681 KB

оптимальное управление

трудовые ресурсы

дуополия Курно

пропорциональный экономический рост

мультиуровневая оптимизация

1. Асеев С.М., Кряжимский А.В. Принцип максимума Понтрягина и задачи оптимального экономического роста // Труды математического института им. В.А. Стеклова. – 2007. – Т. 257. – С. 5–271.

2. Васильева Е.В., Быстрай Г.П., Пономарева Т.В. Мониторинг товарных рынков России: первый год членства в ВТО // Экономические стратегии. – 2014. – Т. 16. – № 10(126). – С. 54–61.

3. Васильева Е.В., Пономарева Т.В. Диагностика чувствительности субъектов Федерации к условиям членства России в ВТО // Экономический анализ: теория и практика. – 2014. – № 20 (371). – С. 16–22.

4. Денисова О.А., Пыхов П.А. Оценка современного и перспективного состояния УрФО с позиций энергетической безопасности // Экономика региона. – 2008. – № S4. – С. 52–61.

5. Найдёнов А.С., Кривенко И.А. Теневая экономика в условиях экономического кризиса: диагностика состояния и прогнозирование последствий // Экономика региона. – 2013. – № 1 (33). – С. 46–53.

6. Найдёнов А.С., Судакова А.Е., Кривенко И.А. Анализ экономической интеграции регионов уральского федерального округа // Экономика и предпринимательство. – 2014. – № 10. – С. 446–450.

7. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. – М.: Физматгиз, 1961. – 391 с.

8. Пыхов П.А. Диагностика природно-ресурсного капитала территории // Экономика региона. – 2013. – № 2. – С. 55–63.

9. Регионы России. Социально-экономические показатели. 2014: Стат. сб. / Росстат. – М., 2014. – 900 с.

10. Чичканов В.П., Судакова А.Е., Кривенко И.А. Анализ нелегального рынка рабского труда в регионах России // Известия высших учебных заведений. Социология. Экономика. Политика. – 2015. – № 1 (44). – С. 80–83.

11. Ane B.K., Tarasyev A.M., Watanabe C. Construction of Nonlinear Stabilizer for Trajectories of Economic Growth // Journal of Optimization Theory and Applications. – 2007. – Vol. 134. – № 2. – P. 303–320.

12. Naidenov A.S., Krivenko I.A. View’s’ Evolution of Western Researchers to Understanding of the Illegal Economy // Журнал экономической теории. – 2014. – № 4. – С. 221–229.

Негативная демографическая ситуация в России предопределила наличие многочисленных проблем рынка труда. Сочетание высоких показателей оборота рабочей силы с низкими показателями оборота рабочих мест составляет важнейшую черту российского рынка. Ввиду сложной социально-экономической ситуации, сложившейся на российском рынке труда в последние годы, неизбежно привлечение трудовых ресурсов из стран ближнего зарубежья [3, 10] в количестве и качестве, необходимом для устойчивого развития системы. В то же время трудовая миграция несет в себе множество рисков и угроз устойчивому развитию экономических систем принимающих территорий [5, 6, 12]. Направленность миграционных потоков претерпевает неизбежные изменения в зависимости от развития социально-экономической ситуации на территориях притяжения [2].

Процесс моделирования оптимального уровня инвестиций в экономику должен также учитывать интенсивность развития региональной экономики, находящуюся в прямой зависимости от состояния энергетической обеспеченности [4] и объема природно-ресурсного капитала территории [8]. По России в целом за период 1994–2013 гг. количество работников организаций, выполнявших научные исследования и разработки (НИР), сократилось практически на треть (рис. 1): численность занятого НИР персонала снизилась на 33,8 % (с 1098,2 тыс. человек в 1994 году до 727,0 тыс. человек в 2013 г.), снижение доли исследователей составило 29,8 %. При этом снижение общей численности населения страны за исследуемый период составило всего около 2,7 %.

Число выполнявших НИР организаций за анализируемый период сократилось лишь на 11,2 % (с 4059 в 1995 г. до 3605 в 2013 г.). Очевидно, что в настоящее время наблюдается процесс значительного сокращения численности научных кадров. На рис. 2 приведены динамика изменения объема инвестиций в основной капитал по сферам образования и науки за период 2000–2013 гг., а также изменение величины внутренних затрат на НИР и объема произведенной в стране инновационной продукции за период 1994–2013 гг. Объем инвестиций в основной капитал по виду экономической деятельности – наука за период 2000–2013 гг. в текущих ценах вырос в 23,2 раза, в сопоставимых ценах – в 5,8 раза.

За период 1994–2013 гг. рост внутренних затрат на исследования и разработки в текущих ценах составил 145,7 раза, в сопоставимых ценах – 4,1 раза; если же считать с 2000 г., то в текущих ценах рост составил 9,8 раза, в сопоставимых ценах – всего 2,6 раза. Для корректировки и повышения отдачи от инвестиционных потоков необходимы научно обоснованные прогнозы, отражающие изменение динамики инвестиций в зависимости от результативности их использования. В качестве основы модели выступает классическая задача оптимального управления инвестициями в капитал [1, 7, 11], которая расширяется за счет блока управления общими затратами, направленными в рынок труда. В данной модели предлагается степенная форма зависимости объема выпуска от трудовых ресурсов, заданная с помощью степенной функции Кобба ‒ Дугласа:

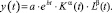(1)

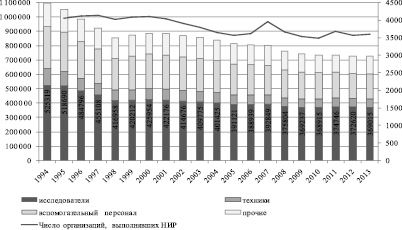
Рис. 1. Число организаций (единиц) и численность работников (человек), выполнявших научные исследования и разработки (по категориям), за период 1994–2013 гг. Источник: составлено по данным Росстата РФ [9]

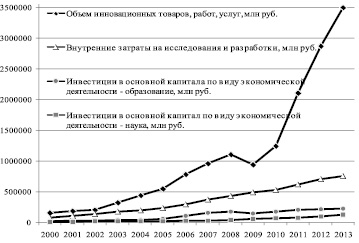
Рис. 2. Объем инвестиций в основной капитал по ВЭД образование и наука за период 2000–2013 гг.; внутренние затраты на исследования, объем инновационных товаров, за период 1994-2013 гг. (в текущих ценах). Источник: составлено по данным Росстата РФ

Производственная функция типа Кобба-Дугласа включает в себя показатели эластичности выпуска α и β к капиталу K = K(t) и трудовым ресурсам L = L(t), а также сомножитель a∙e^bt, возрастающий экспоненциально и определяющий рост объемов выпуска за счет факторов, учтенных в данной модели неявно. Капитал в рамках данной модели соответствует основным фондам, а трудовые ресурсы определяют численность занятого в отрасли населения. Трудовые ресурсы подчинены классической динамике, при которой инвестиционные составляющие, скорректированные на величину обесценивания соответствующего фактора, способствуют росту рассматриваемых показателей.

Предположим, что стоимость трудовых ресурсов определяется на основе уровня ВВП страны и численности занятого на рынке труда населения. Пропорции в модели не являются фиксированными, при этом их динамика зависит от механизма ценообразования, основанного на модели дуополии Курно

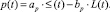
Механизм ценообразования в данной модели представлен как игрок, который устанавливает цену трудовых ресурсов. Приведение параметров модели к относительным величинам позволит выразить скорость роста цен и описать динамику инвестиционных потоков в условиях пропорционального развития описываемой системы. Составим основную пропорцию, определяющую динамику взаимодействия капитала и трудовых ресурсов в данной модели, что позволит максимизировать объем выпуска при заданных затратах:

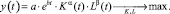
При этом необходимо учесть ряд ограничений на основные параметры модели, обеспечивающих адекватное поведение рассматриваемой системы на конечном и бесконечном горизонтах. Расходы на основные управляющие параметры модели, капитал и трудовые ресурсы ограничены соотношением K(t) + p(t)∙L(t) = C(t), определяющим их линейную зависимость от величины общих затрат.

В результате получаем классическую задачу микроэкономики, аналитическое решение которой возможно получить с помощью метода Лагранжа. Для оптимизационной задачи первого уровня модели справедливо условие пропорциональности между капиталом и трудовыми ресурсами, необходимое для обеспечения сбалансированного состояния экономической системы в модели

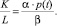
В силу условия однородности, заданного в модели, данное соотношение приводит к линейности оптимального решения относительно общей стоимости. С помощью функции A(t) определяется доля выпуска, полученная за счет факторов, учтенных в модели косвенно. Агрегированная переменная C = C(t) в соответствии с логикой модели, передается на второй уровень для решения задачи управления инвестициями, направленными в капитал и трудовые ресурсы.

Агрегированный показатель скорости роста цен в рамках рассматриваемой системы выражается через скорости роста цен, заданных для основных параметров модели экономического роста:

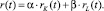(2)

Выразим скорости роста цен для капитала и трудовых ресурсов. В результате получим значения скорости роста цен для заданных управляющих параметров. Приведем инвестиционные потоки для капитала и трудовых ресурсов к упрощенному виду:

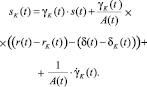(3)

Динамика инвестиций в трудовые ресурсы выражается через величину общих инвестиционных затрат, аналогично описанному выше поведению инвестиционных потоков, направленных в основные фонды:

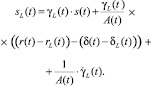(4)

На основании изложенных выше положений составим уравнение баланса, необходимое для выражения абсолютного значения потребления C(t) в относительных величинах. В рамках производственного цикла необходимо как инвестирование в основные фонды, так и покрытие расходов, направленных на трудовые ресурсы. Уравнение баланса регламентирует распределение выпуска на инвестиции I_K(t) = s_K(t)∙y(t) и I_L(t) = s_L(t)∙y(t), описывающие вложения в основной капитал и трудовые ресурсы, а также распределение абсолютного значения потребления:

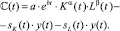(5)

В соответствии с конструкцией модели решения первого уровня агрегируются в стоимостные затраты и передаются на второй уровень оптимизации. Динамическая оптимизация макроэкономических показателей проводится на втором уровне с помощью принципа максимума Понтрягина. Составим функцию полезности для определения качества модельных траекторий на втором уровне оптимизации:

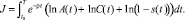(6)

Рассмотрим задачу оптимального управления для инвестиций на втором уровне оптимизации. Данная задача характеризуется максимизацией функции полезности в условиях управляемой системы на траекториях полученных в результате описания следующей динамики:

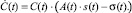(7)

Обобщенная амортизация затрат определяется разностью между агрегированным уровнем обесценивания и скоростью роста цен σ(t) = δ(t) – r(t). На втором уровне оптимизации рассматривается задача оптимального управления для инвестиций. Решением данной задачи в рамках принципа максимума Понтрягина является оптимальный уровень инвестиций, который связывает все блоки модели. Получим аналитические соотношения для оптимального управления посредством подстановки решений уравнений гамильтоновой динамики в структуру оптимального управления. При рассмотрении задачи экономического роста на бесконечном горизонте оптимальное управление задано следующим соотношением:

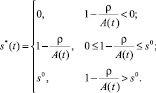(8)

При получении оптимальных инвестиций s*(t) возможно выполнить обратный переход от второго уровня оптимизации к первому уровню, а также определить структуру оптимальных инвестиционных потоков, направленных на обеспечение трудовых ресурсов в соответствии с условиями начальной системы. За счет свойства вогнутости максимизированного гамильтониана по переменной С принцип максимума Понтрягина выделяет траектории, удовлетворяющие условию оптимальности для задачи управления.

Итоговая модель является моделью пропорционального экономического роста, обеспечиваемого оптимальными инвестициями, направленными в основные фонды и на содержание трудовых ресурсов, и может быть использована для эконометрического анализа и прогностического моделирования устойчивого развития стран и регионов при оптимизации потоков инвестиций. Изменение пропорционального соотношения в направленности инвестиционных потоков в различные сферы экономики может привести к последующему дисбалансу экономической системы в целом. Увеличение инвестиционного потока, направленного на повышение уровня инвестиций в науке, впоследствии приведет к повышению отдачи от наукоемких отраслей экономики. Модель целесообразно использовать для выделения основных составляющих экономических систем и определения доли социально-экономических инноваций на уровне региональной экономики, что в результате позволит определить оптимальный уровень потоков инвестиций, необходимый для обеспечения устойчивого социально-экономического развития инновационных сфер экономики.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 14-06-31167мол_а «Формирование механизма управления человеческим капиталом региона в условиях необходимости развития высокотехнологичного сектора экономики»).

Рецензенты:

Андреева Е.Л., д.э.н., профессор, руководитель центра региональных компаративных исследований, Институт экономики Уральского отделения РАН, г. Екатеринбург;

Петров М.Б., д.т.н., доцент, руководитель центра развития и размещения производительных сил, Институт экономики Уральского отделения РАН, г. Екатеринбург.

Библиографическая ссылка