Технологические процессы (ТП), характерные для стадии эксплуатации сложных технических объектов (СТО), как правило, включают в себя две группы операций: операции, без выполнения которых функционирование объекта эксплуатации невозможно, и операции, отказ от выполнения которых приводит только к снижению вероятности достижения цели этих процессов, например вероятности безотказной работы объекта эксплуатации. В тех случаях, когда временных или иных видов ресурсов не хватает для проведения операций ТП в полном объеме, возникает необходимость в отказе от некоторых операций второй группы.
Например, такая ситуация может иметь место при необходимости проведения экстренного пуска ракеты космического назначения (РКН) для замены вышедшего из строя космического аппарата со стартового комплекса (СК), на котором проводится его техническое обслуживание. В этом случае может возникнуть дефицит времени на выполнение ТО оборудования СК в полном объеме, что определяется назначенной датой запуска КА и степенью выполнения ТО к моменту получения приказа на проведение пуска РКН. Описанная ситуация порождает необходимость оперативного решения задачи формирования оптимальной структуры (графика) процесса завершения ТО, обеспечивающей максимальную вероятность своевременного пуска РКН при возникшем дефиците времени на выполнение ТО.
В настоящее время для решения задач структурной оптимизации наиболее широко применяются комбинаторно-логические методы. Эти методы различаются способами описания или способами формирования области перебора возможных структур: с помощью морфологических таблиц [8], альтернативных деревьев [1], ориентированных гиперграфов [2], генетических алгоритмов [5, 9]. Для иерархических структур разработаны оригинальные методы оптимизации с аддитивными целевыми функциями [4, 6]. Все эти методы отличаются большой вычислительной сложностью. Поэтому появились попытки решения задач структурной оптимизации методами дискретной оптимизации. Так, в работе [3] такая задача сведена к задаче булева линейного программирования. Недостатком предложенного в этой работе подхода является использование в качестве целевых функций показателей, которые лишь косвенно и не всегда могут характеризовать качество функционирования объекта исследования. В данной статье предлагается алгоритм структурной оптимизации технологического процесса, разработанный на основе метода дискретного динамического программирования [10] и имеющий полиномиальную сложность [7].
Постановка задачи
Рассмотрим ТП, целью которого является обеспечение надежности СТО при применении, и ситуацию, в которой объем контрольных операций по выявлению отказов подсистем СТО не может быть выполнен полностью из-за необходимости его экстренного применения. Пример такой ситуации был приведен выше.
В подобной ситуации задача структурной оптимизации рассматриваемого ТП на содержательном уровне может быть сформулирована следующим образом: найти перечень операций, исключение которых из ТП позволит реализовать его за директивное время, оставшееся до начала применения СТО TД, и приведет к минимальному снижению вероятности его безотказной работы в ходе применения.
Теперь дадим математическую постановку задачи.
В качестве модели ТП возьмем сетевую модель G = (V, A), где V – множество вершин (событий); ?V? = r – мощность множества V; А – множество дуг (операций); ?А? = n – мощность множества А.
Выделим в множестве А подмножество операций В, которые могут быть исключены из ТП.
Положим, что для каждой дуги (i, j) ? А задана продолжительность tij операции, а для каждой дуги (i, j) ? В задана вероятность qij отказа системы в случае, если на ней не будет проведена операция (i, j), т.е. даны множества Т = {tij: (i, j) ? А}, и Q = {qij: (i, j) ? B}.
После выполнения операции (i, j) на системе будем полагать, что вероятность ее отказа равна 0, так как при ее проведении мы либо убедимся в том, что система неисправна, либо выявим неисправность и устраним ее.
Обозначим через xi,j переменную, которая равна единице, если дуга (i, j) исключена из модели ТП, и равна нулю, если дуга (i, j) оставлена в модели ТП.
Кроме того, введем следующие обозначения:
Ij – множество номеров событий, непосредственно предшествующих событию j ![]() , где r – номер завершающего события);
, где r – номер завершающего события);
Xj – вектор, элементами которого являются переменные xi,j при i ? Ij;
![]() – составной вектор размерности n, представляющий собой упорядоченное множество переменных xi,j.
– составной вектор размерности n, представляющий собой упорядоченное множество переменных xi,j.
С учетом принятых обозначений формальная постановка задачи примет вид
Дано: G, B, T, Q, TД.
Найти
![]() (1)
(1)
при условии
Tr(X*) ? TД,
где Tr(X*) – раннее время наступления завершающего события сетевой модели G, которое может быть вычислено по рекуррентной формуле определения раннего срока наступления j-го события
![]() (2)
(2)
где Ij – множество номеров событий i, непосредственно предшествующих событию j.
В случае, когда СТО являются высоконадежными объектами, вероятность отказов отдельных систем qi,j представляет собой малые величины (< 0,01), можно пренебрегать их произведениями. В этом случае, учитывая выражение (2), задачу (1), можно сформулировать следующим образом.
Найти
![]() (3)
(3)
при условии
![]()
где ?j – ресурс времени, который может быть выделен для выполнения операций, необходимых для достижения события j, при этом ?r = TД.
Структура целевой функции и ограничения задачи (3) позволяют применить для ее решения метод динамического программирования [10].
Алгоритм решения задачи
Обозначим:
Qj(?j) – минимальное значение вероятности безотказной работы систем, на которых выполнены операции, необходимые для достижения события j, при условии, что на их выполнение выделен ресурс времени, равный ?j .
Тогда для первого шага решения задачи можно записать
![]() (4)
(4)
Для последующих шагов функциональное уравнение Беллмана примет вид
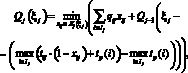
![]() (5)
(5)
Общее число шагов равно r – 1, т.е. на единицу меньше, чем число событий в сетевой модели.
Соотношения (4), (5) используются на этапе прямого хода алгоритма динамического программирования, в результате которого на каждом шаге, т.е. для каждого j, для всех возможных значений ?j определяются условно оптимальные значения ![]() (при условии, что для достижения события j выделен ресурс ?j) и минимальное значение вероятности отказа изделия Qr (?r = TД).
(при условии, что для достижения события j выделен ресурс ?j) и минимальное значение вероятности отказа изделия Qr (?r = TД).
Так как на последнем шаге ?r известно (оно равно TД), то значения, ![]() при которых имеет место минимум вероятности отказа изделия, равный Qr (?r = TД), являются оптимальными, т.е.
при которых имеет место минимум вероятности отказа изделия, равный Qr (?r = TД), являются оптимальными, т.е. ![]() .
.
Значение ![]() позволяет начать этап обратного хода алгоритма динамического программирования. На этом этапе последовательно определяется конкретное значение ресурса ?j, которое может быть выделено для выполнения операций, необходимых для достижения события j (j = r – 1, r – 2, …, 1), при условии, что отказ от операций, выполненных после события j, произведен оптимальным образом. Это может быть сделано по формуле
позволяет начать этап обратного хода алгоритма динамического программирования. На этом этапе последовательно определяется конкретное значение ресурса ?j, которое может быть выделено для выполнения операций, необходимых для достижения события j (j = r – 1, r – 2, …, 1), при условии, что отказ от операций, выполненных после события j, произведен оптимальным образом. Это может быть сделано по формуле
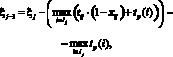 (6)
(6)
где Кj – множество номеров событий k, непосредственно следующих за событием j.
Определив ![]() , находим соответствующие ему значения
, находим соответствующие ему значения ![]() .
.
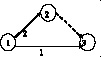
Пример решения задачи. Рассмотрим пример решения задачи (3) для ТП, изображенного на рисунке.
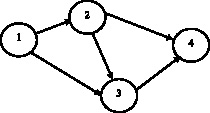
Сетевая модель ТП
Необходимые данные об операциях этого процесса приведены в табл. 1.
Предположим, что в этом примере В = А, т.е. любая из операций ТП может быть исключена. Требуется определить структуры ТП, соответствующие оптимальному исключению операций, в смысле задачи (3), для множества значений директивного времени M = {8, 7, 6, 5, 4, 2}.
Перед началом решения задачи целесообразно предварительно для каждого возможного значения ?j определить множество возможных значений кортежа xj, что позволит уменьшить в дальнейшем объем вычислений. Эти расчеты позволили определить минимальные значения вероятности отказа СТО при каждом значении ТД ? M и соответствующие минимальные значения элементов множества ![]() . Зная
. Зная ![]() , по формуле (6) находим значения элементов множеств
, по формуле (6) находим значения элементов множеств ![]() для j = r – 1, r – 2, …, 2 и формируем оптимальный вектор Х*.
для j = r – 1, r – 2, …, 2 и формируем оптимальный вектор Х*.
Результаты расчетов по формулам (4), (5) приведены в табл. 2.
Таблица 1
Характеристики операций ТП
|
Код операции |
1–2 |
1–3 |
2–3 |
2–4 |
3–4 |
|
Вероятность отказа системы в случае невыполнения операции |
0,002 |
0,002 |
0,001 |
0,004 |
0,003 |
|
Продолжительность операции, ч |
2 |
1 |
4 |
5 |
3 |
Таблица 2
|
Шаг 2 |
Шаг 3 |
|||||||
|
?2 |
Q2(?2) |
|
?3 |
Q3(?3) |
|
x4 |
Q4(x4) |
|
|
0 |
00,002 |
1 |
0 |
00,005 |
<1, 1> |
0 |
00,012 |
<1, 1> |
|
1 |
00,002 |
1 |
1 |
00,003 |
<0, 1> |
1 |
00,012 |
<1, 1> |
|
2 |
00,000 |
0 |
2 |
00,001 |
<0, 1> |
2 |
00,010 |
<1, 1> |
|
3 |
00,001 |
<0, 1> |
3 |
00,010 |
<1, 1> |
|||
|
4 |
00,001 |
<0, 1> |
4 |
00,007 |
<1, 0> |
|||
|
5 |
00,001 |
<0, 1> |
5 |
00,003 |
<0, 0> |
|||
|
6 |
00,000 |
<0, 0> |
6 |
00,003 |
<0, 0> |
|||
|
7 |
00,001 |
<0, 0> |
||||||
|
8 |
00,001 |
<0, 0> |
||||||
Таблица 3
|
Тд, у.е. |
Q(ТД) |
X* = [x12x13x23x24x34]T |
Структура сетевой модели |
|
2 |
0,08 |
[00111]T |
|
|
3 |
0,08 |
[00111]T |
|
|
4 |
0,07 |
[10110]T |
|
|
5 |
0,03 |
[10100]T |
|
|
6 |
0,03 |
[10100]T |
|
|
7 |
0,01 |
[00100]T |
|
|
8 |
0,01 |
[00100]T |
|
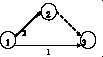
В табл. 3 для каждого значения ТД приведены вероятности отказа изделия, вектор X* и соответствующая ему структура сетевой модели (под стрелками указаны продолжительности операций).
В рассмотренном примере в каждое событие входило не более двух операций. В общем случае множества Ij могут содержать более двух элементов, что может существенно увеличить комбинаторную сложность решаемой на каждом шаге задачи. Чтобы избежать этого, целесообразно преобразовать заданную сетевую модель в модель, в события которой входят не более двух действительных операций. Это всегда можно сделать путем введения дополнительных событий и фиктивных операций.
Заключение
Предложенный в работе алгоритм структурной оптимизации технологических процессов, обеспечивающих эксплуатацию СТО, математическая модель которых может быть представлена ациклическим графом с одним истоком и одним стоком, позволяет получить информацию для обоснования решения об отказе от выполнения ряда операций, например операций контроля, при необходимости сокращения продолжительности этих процессов. Такой информацией является набор операций, исключение которых из технологического процесса позволит применить СТО в заданное время и при этом приводит к минимальному снижению вероятности его безотказной работы в процессе применения. Сопоставлением вероятностей отказов СТО, не выявленных из-за исключения названных операций, и их последствий с оценками ущерба или упущенной выгоды, которые могут иметь место при несвоевременном применении СТО, можно будет определить риск неправильного принятия решения.
Рецензенты:
Петров Г.Д., д.т.н., профессор, начальник кафедры, Военно-космическая академия имени А.Ф. Можайского, г. Санкт-Петербург;
Миронов А.Н., д.т.н., профессор ка федры, Военно-космическая академия имени А.Ф. Можайского, г. Санкт-Петербург.