Во многих технических приложениях возникают задачи о безопасном охлаждении тепловыделяющих материалов. Сюда относится определение характеристик охлаждения, а также критических условий, при нарушении которых имеющиеся способы охлаждения не позволяют снимать выделяющееся в материале тепло, вследствие чего происходит разогрев материала сверх заданных пределов.
Примером такой задачи может служить охлаждение тепловыделяющего пористого материала, погруженного в большой объем воды. Данный случай возникает в атомной энергетике в случае тяжелой аварии с плавлением активной зоны реактора, когда высокотемпературный расплав кориума, взаимодействуя с водяным теплоносителем, фрагментируется на капли, образующие при застывании дисперсные частицы. Выпадающие на поверхность частицы формируют пористую среду, в которой происходит объемное тепловыделение, обусловленное наличием в кориуме продуктов распада. Важной задачей является обеспечение пассивного охлаждения такой среды в объеме воды без возникновения областей локального осушения, поскольку вторичное плавление материала может привести к термическому воздействию на контейнмент реактора и попаданию радиоактивных материалов в окружающую среду [2, 7, 9].
Критические условия охлаждения могут быть получены в аналитическом виде только в одномерной постановке, когда выделяющийся в объеме пар покидает пористый слой на его верхней границе, и через ту же границу в слой поступает замещающая пар вода. В таком случае, как известно, критические условия получаются решением алгебраического уравнения для скоростей фильтрации фаз в условиях противонаправленных потоков [5, 6, 8]. Более сложные геометрические конфигурации необходимо исследовать численными методами [3, 11, 12].
В настоящей работе рассмотрен пример численного моделирования охлаждения осесимметричного пористого объема, поверхность которого имеет гауссову форму. Получены поля многофазного течения (пар, вода) как для случая успешного охлаждения, когда вода смачивает весь объем пористой среды, так и в случае возникновения локального осушения. Определены критические условия охлаждения для различных размеров частиц пористого материала.
Постановка задачи
Рассматривается объем пористого материала (диаметр частиц DP, пористость ε) с равномерно распределенным объемным источником тепла 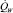 . Пористый материал находится на непроницаемом основании в большом объеме воды (бассейне) глубиной H. Теплосъем обусловлен испарением воды (объемная скорость испарения Γ), движение жидкой (индекс l) и газовой (индекс v) фаз описывается уравнениями неразрывности и нелинейной фильтрации:
. Пористый материал находится на непроницаемом основании в большом объеме воды (бассейне) глубиной H. Теплосъем обусловлен испарением воды (объемная скорость испарения Γ), движение жидкой (индекс l) и газовой (индекс v) фаз описывается уравнениями неразрывности и нелинейной фильтрации:
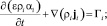 (1)
(1)
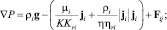 (2)
(2)
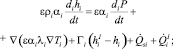 (3)
(3)
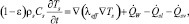 (4)
(4)
здесь αi – объемная доля i-й фазы, ρi и μi – плотности и вязкости фаз; ji – фильтрационные скорости; Γv = –Γl = Γ – скорость испарения на единицу объема; P – давление; g – ускорение силы тяжести; K и η – линейная и квадратичная проницаемости; Kri и ηri – соответствующие относительные фазовые проницаемости; Fij – силы межфазного трения; Ti, hi и λi – температуры; удельные энтальпии и теплопроводности фаз; 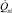 – мощность теплопередачи от дисперсных частиц в i-ю фазу;
– мощность теплопередачи от дисперсных частиц в i-ю фазу; 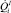 – мощность межфазного теплообмена на единицу объема; Ts, ρs и Cs – температура, плотность и удельная теплоемкость материала дисперсных частиц.
– мощность межфазного теплообмена на единицу объема; Ts, ρs и Cs – температура, плотность и удельная теплоемкость материала дисперсных частиц.
Трение двухфазного потока в пористой среде описывается путем введения линейной и квадратичной проницаемостей [4]:
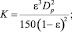
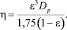 (5)
(5)
Замыкающие соотношения для уравнений (1)–(5), задающие законы трения и теплообмена, подробно рассмотрены в работах [11, 12].
Граничные условия задачи формулируются следующим образом. На всех твердых поверхностях (дно и стенки бассейна) задаются условия непротекания и адиабатичности. На верхней границе расчетной области ставится заданное системное давление Psys. Начальная температура в системе считается равной температуре насыщения при этом давлении T = Tsat(Psys), так что вода у дна бассейна первоначально недогрета вследствие более высокого давления, вызванного гидростатическим давлением столба жидкости.
В данной задаче основной интерес представляет двухфазное течение в пористом объеме, тогда как внешнее течение играет второстепенную роль. Поэтому для описания течения вне пористого объема используется упрощенный подход: вводится некоторая пористая среда, обладающая малым сопротивлением (достигается путем использования большого диаметра частиц и высокой пористости), что позволяет использовать те же уравнения (1)–(5), что и в основном пористом слое, не привлекая полные уравнения двухфазных жидкостей.
Численный метод
Описанная выше математическая модель (1)–(5) реализована программно для двумерного осесимметричного случая. Особенности численной реализации описаны в работах [11, 12]. Используется полностью неявная численная схема первого порядка точности по времени, для пространственных аппроксимаций используется cхема MUSCL второго порядка точности. На каждом шаге значения переменных на верхнем временном слое находятся методом Ньютона путем выполнения глобальных итераций. На каждой глобальной итерации сначала решаются уравнения импульса для компонент скорости фаз, а также находятся коэффициенты, связывающие приращения скорости с приращениями давления и объемного паросодержания. Затем осуществляется линеаризация уравнений неразрывности и энергий фаз, после чего решение полученной системы линейных алгебраических уравнений производится методом PGMRES с предобуславливателем ILUT [1].
Параметры расчетов
Все расчеты проводились при фиксированных размерах бассейна (диаметр 9 м, высота 6 м). Пористая среда занимала объем, ограниченный сверху поверхностью, описываемой гауссовой функцией
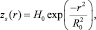
где H0 = 2,5 м; R0 = 1,75 м (общий объем пористой среды при этом составлял 23,7 м3). Пористость среды была постоянной и равной 40 %. При плотности материала (кориума) ρs = 8285,1 кг/м3, при данных параметрах масса тепловыделяющей среды составляет 120 т. Считается, что пористая среда состоит из частиц со средним диаметром DP = 2 мм.
В проведенных расчетах главными варьируемыми параметрами были объемная мощность тепловыделения
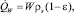
где W – удельная мощность тепловыделения на единицу массы материала) и давление на верхней границе расчетной области Psys. Начальная температура воды в бассейне принималась равной температуре насыщения при давлении Psys, температура пористой среды бралась равной температуре насыщения при локальном давлении (превышающем Psys на величину гидростатического давления). Расчеты проводились на интервале времени 3 часа.
Результаты расчета
Рассмотрим сначала случай, когда скорость тепловыделения относительно невелика, так что охлаждение пористой среды происходит без ее осушения. На рис. 1 показано распределение объемного паросодержания и поля скоростей пара (слева) и жидкости (справа) в момент времени t = 3600 c для случая Psys = 1,3 бар, W = 100 Вт/кг (при этом 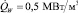 ). Отметим, что в отсутствие осушения стационарные распределения параметров устанавливаются в течение нескольких первых минут; тем не менее, расчеты проводились в течение часа физического времени, чтобы убедиться в том, что не происходит медленного изменения паросодержания, приводящего к возникновению осушенных зон.
). Отметим, что в отсутствие осушения стационарные распределения параметров устанавливаются в течение нескольких первых минут; тем не менее, расчеты проводились в течение часа физического времени, чтобы убедиться в том, что не происходит медленного изменения паросодержания, приводящего к возникновению осушенных зон.
Из рис. 1 видно, что максимальное паросодержание достигается в верхней части пористого объема, при этом максимальная объемная доля пара составляет 80 %. Выделяющийся пар движется практически вертикально, образуя над вершиной пористого объема нагретую струю. Видно также, что в окружающем пространстве развивается циркуляционное течение жидкости. Важно отметить, что внутри пористого объема течение жидкости происходит снизу вверх, хотя и с малыми скоростями. Следовательно, в двумерном (и пространственном) случае имеет место не противоток пара и воды (как в случае плоского слоя), а их сонаправленное течение.
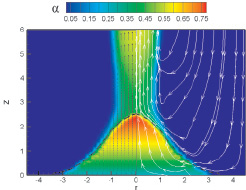
Рис. 1. Стационарное распределение паросодержания в пористой среде при объемной мощности тепловыделения 0,5 МВт/м3; векторами показана скорость газа (слева), линиями тока – скорость жидкости (справа). Граница тепловыделяющей среды показана штриховой линией
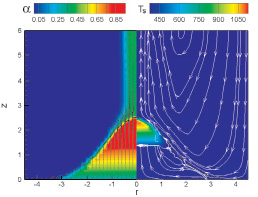
Рис. 2. Распределение паросодержания (слева) и температуры пористой среды при объемной мощности тепловыделения 1,24 МВт/м3; векторами показана скорость газа (слева), линиями тока – скорость жидкости (справа). Граница тепловыделяющей среды показана штриховой линией
Рассмотрим теперь случаи, когда в пористом объеме возникает осушенная область. На рис. 2 представлены распределения паросодержания (слева) и температуры пористой среды (справа) при удельной мощности тепловыделения при тепловыделении, превышающем критический порог: представленные результаты соответствуют моменту времени t = 3 часа для случая Psys = 3 бар, W = 250 Вт/кг (при этом 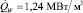 ). Отметим, что при увеличении давления осушение пористой среды возникает при более высоких мощностях тепловыделения, поскольку выделяющийся пар обладает большей плотностью и меньшим удельным объемом, что облегчает его истечение из пористой среды и замещение водой.
). Отметим, что при увеличении давления осушение пористой среды возникает при более высоких мощностях тепловыделения, поскольку выделяющийся пар обладает большей плотностью и меньшим удельным объемом, что облегчает его истечение из пористой среды и замещение водой.
Из рис. 2 следует, что осушение происходит в верхней части пористого объема, при этом движение пара носит практически вертикальный характер. Максимальный разогрев частиц составляет 1200 К, что, однако, недостаточно для вторичного плавления материала, при этом максимум температуры достигается в верхней точке пористого объема. Линии тока жидкости показывают, что в нижней части пористой среды направление течения жидкости по-прежнему совпадает с направлением течения пара, так что условия противотока фаз не возникают нигде.
На рис. 4 показаны зависимости относительной высоты осушенной зоны
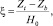
(где Zt и Zb – координаты верхней и нижней границ осушенной области на оси симметрии) от удельной мощности тепловыделения W, полученные в расчетах при системном давлении Psys = 1,3 и 3 бар. Для каждого давления расчетные точки хорошо аппроксимируются линейной функцией. Экстраполяция данной линейной функции к нулевому значению ξ дает критическое значение мощности тепловыделения, составляющее для указанных давлений W0 = 104,2 и 133,7 Вт/кг соответственно (при этом объемная мощность тепловыделения равна 0,518 и 0,665 МВт/м3).
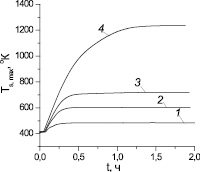
Рис. 3. Зависимость от времени максимальной температуры пористой среды при системном давлении 3 бар для удельных мощностей тепловыделения W = 160 Вт/кг (1), 180 Вт/кг (2), 200 Вт/кг (3) и 250 Вт/кг (4)
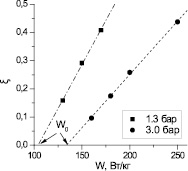
Рис. 4. Зависимость относительного размера осушенной зоны от удельной мощности тепловыделения для различных системных давлений. Стрелками показаны критические значения мощности
Заключение
Расчеты показывают, что для двумерных конфигураций осушенная область возникает в верхней части пористого слоя, что значительно отличается от одномерного случая, когда осушение начинается с «захлебывания» противоположно направленного потока воды и пара на верхней границе, после чего первоначальное пересыхание возникает в нижней части пористого слоя. Дальнейшие численные расчеты будут посвящены построению карты режимов, которая будет охватывать практически значимые диапазоны по свойствам пористой среды (диаметр частиц, пористость, давление), размерам и форме пористого объема.
Библиографическая ссылка
Якуш С.Е. КРИТИЧЕСКИЕ УСЛОВИЯ ВОДЯНОГО ОХЛАЖДЕНИЯ ТЕПЛОВЫДЕЛЯЮЩИХ ПОРИСТЫХ СРЕД // Фундаментальные исследования. – 2015. – № 12-6. – С. 1163-1167;URL: https://fundamental-research.ru/ru/article/view?id=39749 (дата обращения: 20.04.2024).



