Известно [5], что в задаче размещения предприятий при планировании развития отрасли имеется m пунктов (пункты производства), в которых расположены или могут быть размещены предприятия одной отрасли. Потребности в товаре, произведенном на этих предприятиях, известны в n пунктах (пункты потребления). Затраты по производству и транспортировке единицы продукта считаются также известными. Задача состоит в определении мест расположения новых предприятий, объемов производства и перевозок так, чтобы суммарные издержки были минимальны.
Многие задачи планирования сводятся к следующей задаче математического программирования (см., например, [8]). Требуется определить вектор x = (x1, x2, ..., xn), обращающий в минимум функцию
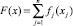
при условиях
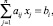i = 1, 2, ..., m;
αj ≤ xj ≤ βj; j = 1, 2, ..., n.
Здесь целевая функция F(x) характеризует суммарные затраты производства, а условия являются балансными соотношениями между продукцией разных предприятий. Благодаря балансным соотношениям гарантируется требуемый объем производства предприятий и устанавливаются ограничения на объемы продукции каждого предприятия, порождаемые учитываемыми потребностями.
Особенностью описываемой задачи оказывается то, что целевая функция является кусочно-линейной функцией [8]. Более того, fj(xj) – выпуклые функции, а значит [6], они полиэдральные функции.
Помимо специфики задачи, приводящей к кусочно-линейному характеру оптимизируемого показателя качества, отметим также наличие и других причин, приводящих к подобному эффекту. Укажем здесь в качестве примеров [2] и переменную технологию производства, и экономию на масштабах производства, и некоторые особенности в технологии производств.
Таким образом, видно, что задачи размещения предприятий приводят к задачам кусочно-линейного программирования (КЛП). Основные положения КЛП можно найти в работах [8, 7, 3]. Отметим, что в упомянутых работах ограничения при оптимизации целевой функции рассматривались в виде неравенств. В данной статье речь идет о задаче планирования производства. Ограничения, которые возникают в таких задачах, как уже отмечалось, имеют вид балансных соотношений.
Цель данной работы – изучение задач КЛП с ограничениями-равенствами, адаптация метода линейной аппроксимации [4] к задаче КЛП с ограничениями отмеченного типа.
Постановка задачи. Решение в общем виде
Рассмотрим следующую задачу линейного программирования. Минимизировать функцию
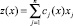(1)
при следующих ограничениях:
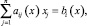
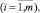(2)
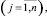(3)
где aij(x), bi(x) и cj(x) – некоторые кусочно-постоянные функции вектора x, принимающие для определенных значений переменной x разные значения.
Будем считать, что функции aij(x), bi(x) и cj(x) определены на одном и том же множестве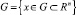 
, и существует такое конечное разбиение 
, 
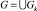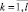, что в каждом подмножестве Gk эти функции постоянны, причем Gk и Gm, k ≠ m, могут пересекаться только по своим границам.
В введении статьи приводилась задача, в которой коэффициенты зависели лишь только от одной компоненты вектора x и носили кусочно-линейный характер. Такая ситуация возникает [8] и в других случаях. Этот факт говорит о том, что в качестве областей Gk имеет смысл брать области типа параллелепипедов (очевидно, что это еще и упрощает описание поиска решения задачи). Поэтому потребуем следующих дополнительных условий на области G и Gk. Будем считать, что G – параллелепипед:
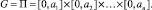
Таким образом, условие (3) можно не рассматривать. Пусть также каждое Gk является параллелепипедом, грани которого параллельны координатным гиперплоскостям. Более того, будем считать, что выполнено следующее требование: существует конечное разбиение параллелепипеда П, например
,
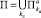
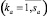где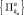 
– набор параллелепипедов, на каждом из которых функции aij(x) являются постоянными. Аналогично можно представить
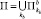
или
,
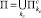
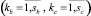где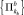 
и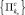 
– конечные наборы параллелепипедов с постоянными bi(x) и cj(x) соответственно. Из этого следует, что существует конечное разбиение множества G = П на параллелепипеды
,
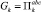такое, что
,
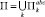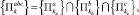
а функции aij(x), bi(x) и cj(x) постоянны для каждого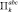 
. При этом соседние параллелепипеды 
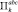и 
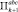пересекаются только по границе.
Наконец, потребуем, чтобы в задаче (1)–(3) целевая функция z(x) и функции ограничений
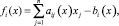i = 1, 2, ..., m,
были выпуклыми функциями. Заметим, что такое ограничение обеспечивает непрерывность функций в П. Это следует из вида функций и непрерывности выпуклой функции во внутренности П [1].
Приведем условие, гарантирующее выпуклость функции
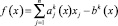
в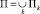 
с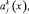 
bk(x), постоянными в каждом из Пk. В этих обозначениях имеет место следующая
Теорема 1
Пусть непрерывная функция f(x) в любой точке x ∈ П удовлетворяет условию
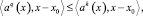.q,
k ∈ S(x), x0 ∈ Пq.
Тогда функция f(x) – выпуклая функция.
Здесь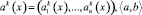 
– скалярное произведение векторов a и b; S(x) – множество индексов таких, что из k ∈ S(x) следует x ∈ Пk.
Доказательство. Прежде всего заметим, что, в силу характера рассматриваемой функции, выполнение свойства выпуклости достаточно доказать локально. Другими словами, если для каждой точки П существует некоторая окрестность, в которой рассматриваемая функция f(x) выпукла, то f(x) выпукла и в П.
Убедимся в том, что функция f(x) локально выпукла. Это свойство, в силу кусочно-линейности функции f(x), надо проверять только для точек, являющихся точками пересечения Пk. Пусть x – одна из таких точек, а x1, x2 лежат в достаточно малой окрестности x. Будем считать, что
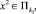
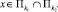
Пусть α ∈ [0; 1] и, для определенности,
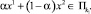
Тогда
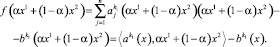
Из непрерывности функции f(x) в точке x следует равенство
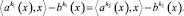
Используя это соотношение, получим
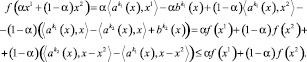
Теорема 1 доказана.
Можно выделить несколько методов решения задачи (1)–(3) в такой постановке.
Самым очевидным из них [2] является простой перебор всех параллелепипедов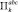 
, так как в каждом из 
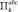мы будем иметь дело с обычной задачей линейного программирования с линейной целевой функцией и выпуклой областью допустимых решений. Для каждого 
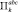находится оптимальный план xk, а решением задачи (1)–(3) является x*, для которого целевая функция минимальна:
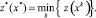
Метод линейной аппроксимации
Для задачи (1)–(3) представляется возможным несколько сократить предложенную схему решения.
Возьмем более простую постановку задачи. Требуется минимизировать выпуклую функцию
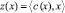(1′)
при линейных ограничениях
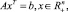(2′)
где c(x) = (c1(x), c2(x), ..., cn(x)), ci(x) (i = 1, ..., n) кусочно-постоянные функции в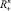 
, 
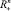– неотрицательный ортант Rn; A ? матрица размера m×n; b ? m-мерный вектор.
Условие (2′) берется здесь вместо (2) и (3) для упрощения изложения. То же, что замена параллелепипеда П на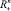 
не уменьшает общности, объясняется существованием у функции z(x) непрерывного продолжения с П на 
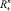. В самом деле, пусть 
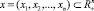и x ∉ П. Пусть x = ak уравнение той грани параллелепипеда П, которую пересекает отрезок с концами в точках 0 и x (в дальнейшем такие отрезки будем отображать [0, x]). Очевидно, что точкой пересечения отрезка [0, x] с гранью является точка αkx/xk. Положим
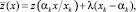
где λ есть произвольное положительное число.
Покажем, что функция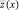 
является выпуклой функцией в конусе K, образованном лучами, проведенными из нуля и пересекающими одну и ту же грань с уравнением x = αk. Возьмем две точки x1, x2 ∈ K/П. Обозначим через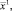 
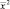точки пересечения грани x = αk с отрезками [0, x1] и [0, x2] соответственно. В силу выпуклости функции z(x) на П имеем с α, α ∈ [0, 1],
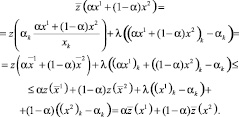
Таким образом, функция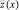 
является непрерывным продолжением с П на 
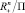функции z(x), выпуклым в конусах типа K.
Определим теперь субдифференциал функции
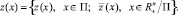
Имеет место
Теорема 2
Субдифференциал ∂z(x) функции z(x) имеет вид
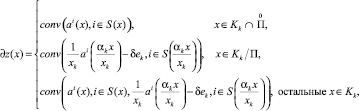
где convG ? выпуклая оболочка множества G;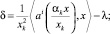 
ek ? вектор, k-я координата которого равна единице, а все остальные равны 0; 
– внутренность П.
Доказательство первой части теоремы можно найти в [7]. Соотношения же для множеств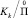 
получатся непосредственно с помощью формул из [1].
Опишем теперь алгоритм метода линейной аппроксимации.
Рассмотрим конус Kk. Множество точек этого конуса можно рассматривать как образ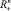 
при отображении линейным оператором с матрицей Qk, т.е. 
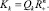Таким образом, чтобы найти минимум функции z(x) в конусе Kk, нужно найти минимум функции z(QkyT) в 
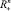. Отметим также, что при этом формулы для субдифференциалов отображений z(x) и z(QkyT) связаны соотношением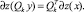 
Опишем теперь алгоритм метода линейной аппроксимации. Здесь, как уже показано, можно считать, что задача задана соотношениями (1′), (2′). Идея метода [1] заключается в том, что в любой допустимой точке xk функция z(x) аппроксимируется функцией zL(x), где zL(x) = z(xk) + g(xk)(y – xk), где g(xk) соответствующим образом выбранный вектор из множества ∂z(xk).
Отметим, что минимизация такой функции эквивалентна в смысле решения минимизации функции g(xk)yT при AyT = b, y ≥ 0. Обозначим решение yk.
Направление g(xk) естественно взять направлением наискорейшего спуска функции z(x) в точке xk. Оно задается вектором g(xk) ∈ –∂z(xk), лежащем на кратчайшем расстоянии от начала координат.
Далее с помощью направления dk = yk – xk получим точку xk+1 как решение задачи минимизации z(xk + τ(yk – xk)), τ ∈ [0, 1]. Все точки вида xk + τ(yk – xk), τ ∈ [0, 1] допустимы в силу выпуклости допустимого множества.
Пусть решение этой задачи есть xk+1. Если окажется, что g(xk+1)(yk+1 – xk+1)T > 0, то процесс продолжается дальше. Если же выполняется обратное неравенство, то в точке xk+1 выполняется условие Куна – Таккера и алгоритм завершает свою работу.
Выводы
Описана модификация задачи размещения предприятий при планировании развития отрасли в виде задачи кусочно-линейного программирования.
Для решения описанной задачи к ее условиям адаптирован метод линейной аппроксимации.
Библиографическая ссылка
Гаврилова М.О., Новоселова Ю.В., Севодин М.А. ОБ ОДНОЙ МОДИФИКАЦИИ ЗАДАЧИ РАЗМЕЩЕНИЯ ПРЕДПРИЯТИЙ ПРИ ПЛАНИРОВАНИИ РАЗВИТИЯ ОТРАСЛИ // Фундаментальные исследования. – 2016. – № 2-1. – С. 125-129;URL: https://fundamental-research.ru/ru/article/view?id=39893 (дата обращения: 25.04.2024).