В настоящее время для создания высокоточного электропривода все чаще применяются цифровые системы управления, в которых используются цифровые датчики [5]. Но в некоторых условиях невозможно использовать цифровые датчики скорости и положения ротора (космос, агрессивные среды, среды с высокой степенью излучения). В таких электроприводах используются аналоговые датчики по типу синусно-косинусного вращающегося трансформатора (СКВТ). Кроме того, при модернизации электроприводов, если в него интегрируется цифровая система управления, необходимо согласование с ней аналоговых датчиков.
Современные системы определения угла положения и скорости вращения ротора по гармоническим сигналам СКВТ отличаются узким диапазоном работы, большой погрешностью, низкой адаптивностью к другим электроприводам, а также слабой защитой от шумов при низком уровне сигнала. К тому же очень мало преобразователей угол-код формируют код скорости вращения вала, что тоже является очень важной координатой при управлении двигателем. В связи с вышеуказанными проблемами целью работы было создание высокоточного преобразователя угол-код, обладающего высокой адаптивностью при интеграции её в электроприводах, большим диапазоном работы и высокой стабильностью выходных характеристик.
В настоящее время наиболее известны два типа преобразователей угол-код [4]:
– фазовые цифровые преобразователи угла (ФЦПУ);
– амплитудные цифровые преобразователи угла (АЦПУ).
Эти преобразователи имеют множество вариантов и модификаций. СКВТ в каждом канале отсчета находятся две взаимно ортогональные обмотки и одна синфазная. Если на ортогональные обмотки одного из каналов отсчета подать прецизионное квадратурное напряжение, то датчик будет работать в фазовом режиме ФЦПУ и при этом можно использовать только один канал отсчета во избежание взаимовлияния каналов. Для построения двухотсчетной системы на базе ФЦПУ требуются два датчика, однако это приводит к ухудшению массогабаритных характеристик. Кроме того, фазовые системы отсчета уступают амплитудным по разрешающей способности выходного сигнала. Исходя из этого, целесообразно использовать амплитудный способ преобразования сигнала угла в цифровой код, для этого существуют два известных типа АЦПУ:
– преобразователи, основанные на тангенциальном преобразовании;
– следящие фазовые преобразователи сигналов (ФПС).
Функциональная схема тангенциального АЦПУ показана на рис. 1.
Принцип работы системы основан на тригонометрических преобразованиях [2] гармонических сигналов, поступающих с СКВТ. Перед подачей сигналов с СКВТ на микроконтроллер их необходимо оцифровать. Так как АЦП микроконтроллера не поддерживает входной сигнал отрицательной полярности, то перед подачей на микроконтроллер аналоговые гармонические сигналы с помощью блоков смещения БС1, БС2, БС5, БС6 необходимо сместить относительно нуля, чтобы сигнал имел только положительную полярность. После оцифровки эти сигналы с помощью блоков смещения БС3, БС4, БС7, БС8 смещаются обратно симметрично относительно нуля. Затем в микроконтроллере происходит деление сигналов синусов и косинусов и вычисление арктангенсов этих величин, т.е. значение углов аналоговых сигналов. В блоках вычисления БВ1 и БВ2 определяется, в каком квадранте находятся вычисленные значения углов согласно следующим условиям:
если sin(φ) > 0 & cos(φ) > 0,
тогда φ = arctg(φ);
если cos(φ) < 0,
тогда φ = arctg(φ) + π;
если sin(φ) < 0 & cos(φ) > 0,
тогда φ = arctg(φ) + 2π.
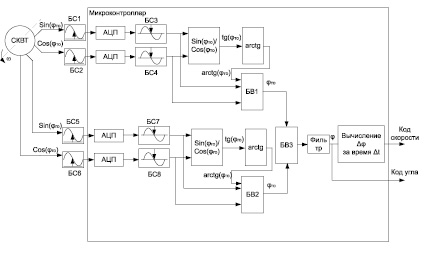
Рис. 1. Функциональная схема тангенциального АЦПУ: БС1, БС2, БС5, БС6 – блоки смещения аналогового сигнала относительно 0; АЦП – аналогово-цифровые преобразователи, встроенные в микроконтроллер; БС3, БС4, БС7, БС8 – блоки (программы) смещения аналогового сигнала симметрично 0; arctg – блок (программа) вычисления арктангенса; БВ1 и БВ2 – блоки (программы) вычисления углов каналов точного отсчета (ТО) и грубого отсчета (ГО); БВ3 – блок (программа) вычисления угла положения вала
В результате на выходе блоков вычисления БВ1 и БВ2 сформированы пилообразные характеристики. Эти характеристики соответствуют изменению углов аналоговых сигналов каналов точного и грубого отсчетов СКВТ. Вычисление положения вала происходит в блоке вычисления БВ3 согласно условию [3]:
если 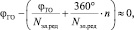
тогда 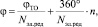 (1)
(1)
где Nэл.ред – коэффициент электрической редукции СКВТ; n = 1...Nэл.ред, изменяется последовательным перебором чисел.
Вычисление кода скорости происходит по формуле
ω = Δφ/Δt. (2)
Точность преобразования и стабильность выходного кода зависят от разрядности АЦП и емкости выходного фильтра, а также от количества задействованных разрядов для вычисления арктангенса. Таким образом, с уменьшением погрешности преобразователя будет уменьшаться быстродействие и, как следствие, будет увеличиваться динамическая ошибка.
В качестве второго варианта для построения преобразователя угол-код можно использовать следящий преобразоватиель тангенсного типа, функциональная схема которого представлена на рис. 2.
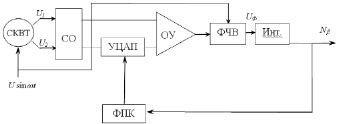
Рис. 2. Функциональная схема следящего тангенциального АЦПУ: СО – селектор октантов; УЦАП – умножающий цифро-аналоговый преобразователь; ФПК – функциональный преобразователь кодов; ОУ – операционный суммирующий усилитель; ФЧВ – фазочувствительный выпрямитель; Инт. – интегратор
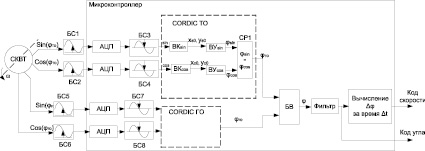
Рис. 3. Функциональная схема преобразователя на методе CORDIC: БС1, БС2, БС5, БС6 – блоки смещения аналогового сигнала относительно 0; АЦП – аналогово-цифровые преобразователи, встроенные в микроконтроллер; БС3, БС4, БС7, БС8 – блоки (программы) смещения аналогового сигнала симметрично 0; ВКsin и ВКcos – блок (программа) вычисления начальных координат векторов; ВУsin и ВУcos – блоки (программы) вычисления углов синуса и косинуса по методу CORDIC; СР1 – блок (программа) сравнения рассчитанных значений углов синуса и косинуса; БВ – блок (программа) вычисления истинного значения угла положения вала
В результате преобразования сигналов напряжение на выходе ФЧВ, приведенное к первому октанту, можно определить по следующему выражению:
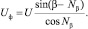 (3)
(3)
Это напряжение является сигналом ошибки замкнутого контура через ФПК. С помощью интегратора Инт. это напряжение в установившемся режиме равно нулю, вследствие чего возникает равенство между выходным кодом преобразователя Nβ и углом положения β, выраженным в двоичном коде. Максимальное значение статической погрешности данного АЦПУ можно определить по формуле
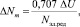 (4)
(4)
где ΔU – погрешность УЦАП; Nэл.ред – коэффициент электрической редукции СКВТ.
К сожалению, существенным недостатком этой системы является сложная реализация на микроконтроллере из-за последовательности производимых расчетов и в результате наличия временного сдвига между входным и выходным значениями, а достоинством является отсутствие статической погрешности.
В последнее время широкое распространение получили методы расчета векторных и тригонометрических функций, основанные на CORDIC. CORDIC (от англ. Coordinate Rotation Digital Computer – цифровой вычислитель поворота системы координат) – вычислитель, основанный на итерационном методе сведения прямых вычислений сложных функций к выполнению простых операций сложения и сдвига [1].
Такой подход особенно полезен при вычислении тригонометрических функций на микроконтроллерах или программируемых логических схемах. Поскольку шаги однотипны, то при аппаратной реализации алгоритм поддаётся развёртыванию в конвейер либо свертыванию в цикл.
Функциональная схема преобразователя, основанного на методе CORDIC, приведена на рис. 3.
Вычисление угла сводится к арифметическим операциям сложения и вычитания, для этого значение синуса в блоке вычисления ВКsin преобразуется в эквивалентный вектор с координатами ys0, xs0. Далее в блоке вычисления ВУsin происходит вычисление угла согласно системе уравнений
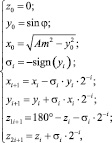 (5)
(5)
где Am – амплитудное значение гармонического сигнала.
Когда yi ≈ 0, значит
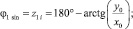
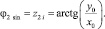
Вычисление угла сводится к «стягиванию» эквивалентного вектора синусоиды к оси абсцисс, при этом одновременно происходит последовательное сложение переменной z, которая и является значением угла эквивалентного вектора. Таким образом, при у = 0 переменная z является углом синусоиды.
По аналогичным формулам рассчитывается угол для косинуса, так как в гармонических сигналах синуса и косинуса одному значению модуля вектора соответствуют два значения угла, в блоке сравнения СР1 сравниваются величины рассчитанных углов для синуса и косинуса и совпавшее значение является истинным значением угла. Алгоритм расчета значения угла приведен на рис. 4.
В результате простых арифметических операций происходит «стягивание» вектора к оси х, тем самым одновременно вычисляется угол вектора, который равен углу гармонического сигнала. В блоке вычисления БВ происходит вычисление угла положения ротора согласно формуле (1). Точность определения угла растет с увеличением разрядности значений переменной y, но в отличие от тангенциального АЦПУ увеличение разрядности переменных не влияет на быстродействие и динамическую ошибку преобразователя.
Таким образом, анализ известных схем преобразователей угол-код показал, что тангенциальные АЦПУ имеют малую статическую погрешность за счет уменьшения быстродействия и увеличения динамической погрешности, а следящие АЦПУ имеют низкие статическую и динамическую погрешности, но только при реализации на дискретных элементах с высокими быстродействием и точностью, что приводит к ухудшению массо-габаритных показателей, увеличению потребления и снижению надежности.
Заключение
1. За счет использования в алгоритме работы CORDIC простых алгебраических вычислений преобразователь на его основе имеет все преимущества тангенциального АЦПУ и лишен его недостатка в виде уменьшения быстродействия с увеличением точности.
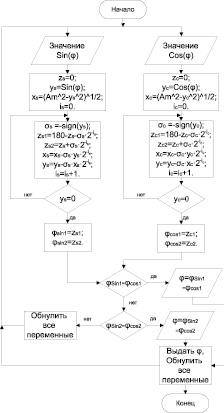
Рис. 4. Алгоритм CORDIC для расчета угла
2. Преобразователь на основе вычислений по методу CORDIC полностью адаптивен и может быть интегрирован в любой электропривод, имеющий в своем составе синусно-косинусный вращающийся трансформатор.
3. Особенностью является независимость входных сигналов от помех и искажений, потому что внутри микроконтроллера можно предусмотреть подпрограммы для защиты от нежелательных искажений и помех.
Библиографическая ссылка
Болгов И.С., Дементьев Ю.Н. ПРЕЦИЗИОННЫЙ ПРЕОБРАЗОВАТЕЛЬ С ФУНКЦИЕЙ ФОРМИРОВАНИЯ КОДА СКОРОСТИ ВРАЩЕНИЯ В СОВОКУПНОСТИ С ИНДУКЦИОННЫМ ДАТЧИКОМ УГЛА // Фундаментальные исследования. – 2016. – № 7-1. – С. 9-13;URL: https://fundamental-research.ru/ru/article/view?id=40449 (дата обращения: 19.04.2024).



