На сегодняшний день в России по способу трелевки можно выделить три вида технологий заготовки древесины: в деревьях, хлыстах и сортиментах. Работа по любой из них в условиях лесной пересеченной местности связана с риском возникновения таких аварийных ситуаций, как опрокидывание машины в результате потери устойчивости, падение на ее кабину массивных предметов – деревьев, сучьев и др., что влечет за собой опасность нанесения травм оператору. Стандартом ИСО 8082, регламентирующим требования к безопасности операторов лесных машин, предписывается оснащать кабины устройствами защиты при опрокидывании (ROPS – Roll-over protective structures) для снижения риска травмирования оператора в случае возникновения аварийной ситуации.
В процессе проектирования, когда разработчиком рассматривается большое количество возможных вариантов исполнения ROPS, приходится решать двоякую задачу: с одной стороны, необходимо создавать новые, более эффективные и менее дорогостоящие конструкции; с другой – разрабатывать методы повышения качества их функционирования и конкурентоспособности. Таким образом, возникает задача оптимизации параметров ROPS, решение которой, во-первых, позволит обеспечить соответствие значений характеристик безопасности требованиям действующих стандартов при проектировании, во-вторых, снизить затраты при изготовлении и эксплуатации конструкции.
Теория катастроф, интенсивно развивающаяся со второй половины ХХ века, основоположниками которой являются французский математик Р. Том [6] и российский математик В.И. Арнольд [1], дает возможность описания качественных (скачкообразных) изменений моделируемой системы при плавных изменениях параметров управления. Одной из семи элементарных катастроф по Р. Тома [6] является катастрофа сборки, потенциальная функция которой определяется
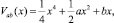
где x – переменная состояния; a, b – переменные управления.
Многообразие M катастрофы задается уравнением
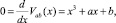
которое имеет от одного до трех вещественных корней. Природа этих корней зависит от дискриминанта
D = 4a3 + 27b2.
Катастрофа происходит, когда дискриминант D меняет знак с отрицательного на положительный [2]. В работе [3] для оценки вероятности катастрофы сборки предложен метод статистической линеаризации для варианта, при котором переменные управления являются случайными величинами. В данном случае оценки математического ожидания и дисперсии дискриминанта D определяются
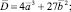
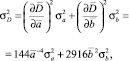
где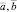 
– математические ожидания переменных управления; 
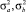– дисперсии переменных управления.
Методы оценки вероятности безотказной работы применительно к устройству защиты оператора при опрокидывании лесной машины представлены в работах [2, 5], и следующим шагом является постановка и решение задачи оптимизации параметров ROPS путем поиска оптимальных значений переменных управления катастрофы сборки.
Постановка задачи оптимального проектирования с применением статистической катастрофы сборки
Постановка задачи оптимального проектирования включает: выбор целевой функции, определение системных ограничений, выбор оптимизируемых параметров. Как правило, невозможно обеспечить максимальную надежность и минимальную стоимость изготовления машины или отдельных ее частей. Следовательно, целесообразно выбирать такой показатель эффективности, который бы учитывал как надежность в период эксплуатации, так и стоимость изготовления.
Монокритериальная задача условной оптимизации может быть сформулирована в виде: минимизировать суммарные затраты, включающие стоимость производства металлоконструкции устройства защиты и потери от простоя лесозаготовительной машины в случае отказа ROPS [3, 4]
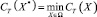
при условиях Xmin ≤ X ≤ Xmax – областные ограничения; F(X) ≤ 0 – функциональные ограничения.
Здесь CT – общие (суммарные) ожидаемые затраты;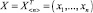 
– вектор параметров проектирования; X* – оптимальное значение вектора параметров проектирования, доставляющее минимальное значение целевой функции; Ω – область допустимых значений вектора X.
В качестве параметров проектирования могут выступать размеры конструкции, механические свойства материалов, допуски на изготовление, величина дефектов и т.д.
Среднее значение суммарных ожидаемых затрат в общем виде может быть выражено как
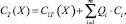
где C1T(X) – затраты на изготовление; Ci, Qi – соответственно стоимость и вероятность отказа i-го вида; m – общее число возможных видов отказов.
Переменные управления катастрофы сборки зависят от параметров проектирования
a = fa(X); b = fb(X).
В свою очередь, вероятность безотказной работы конструкции также может быть выражена через переменные управления катастрофы сборки
R(a, b) = 1 – Q(a, b),
где Q(a, b) – вероятность отказа (вероятность катастрофы сборки).
Таким образом, переменные управления (a, b) могут выступать в качестве оптимизируемых параметров. В качестве областных ограничений принимаются ограничения на размеры деталей; в качестве функциональных – ограничения на площадь поперечного сечения профиля, используемого при изготовлении ROPS. При допущении о нормальном распределении параметров управления вероятность катастрофы сборки выразится
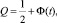
где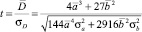 
– значение переменной в функции Лапласа.
Тогда
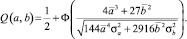(1)
Построение целевой функции
В случае, если преобладающим видом отказа является разрушение конструкции (когда имеет место катастрофа сборки), суммарные ожидаемые затраты, выступающие в роли целевой функции, могут быть выражены как сумма затрат на производство конструкции устройства защиты и стоимости ее отказа с учетом вероятности катастрофы сборки
CT(a, b) = C1T + Q(a, b)·C2T. (2)
Здесь C1T – затраты на производство устройства защиты; C2T – стоимость отказа.
Затраты на производство ROPS определяются как
C1T = C11 + C12, (3)
где C11 – стоимость материала; C12 – стоимость изготовления.
Как первая, так и вторая составляющая затрат на производство могут быть выражены через массу металлоконструкции. Как правило, в прайс-листах, размещенных на сайтах заводов-производителей металлопроката, цены на изготовление металлоконструкций и цены на металлопрокат указаны в рублях за 1 тонну. Таким образом, суммарные затраты на производство можно определить, зная массу ROPS mROPS (кг), а также цену 1 т металлопроката С1 т м/п и цену изготовления 1 т металлоконструкции ROPS С1 т изг
C1T = (С1 т м/п + С1 т изг)·mROPS/1000.
Зависимость затрат на производство от управляющих переменных применительно к ROPS колесного скиддера ТЛК 4-01 (рисунок) может быть представлена в виде
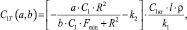(4)
где k1, k2 – коэффициенты в уравнении регрессии A1 = k1•S + k2; A1, C1 – характеристики жесткости ROPS [5]; Fmin – минимальная нагрузка (по ИСО 8082); R – опорная реакция; l – суммарная длина стержней, составляющих конструкцию; S – площадь поперечного сечения стержня; C1 кг – стоимость изготовления 1 кг ROPS, C1 кг = (С1 т м/п + С1 т изг)/1000; ρ – плотность стали.
Стоимость отказа C2T может быть выражена как сумма потерь от простоя лесозаготовительной машины в течение k машиносмен, затрат на перевозку лесозаготовительной машины в мастерскую C2T2, затрат на монтаж (демонтаж) кабины С2T3 и затрат на производство нового устройства защиты оператора C2T4:
C2T = k·С2T1 + C2T2 + С2T3 + C2T4, (5)
где С2T1 – потери от простоя лесозаготовительной машины в течение одной машиносмены.
Таким образом, необходимо найти оптимальное значение вектора параметров проектирования X*, которому при заданных ограничениях соответствует наименьшее значение суммарных ожидаемых затрат. Поскольку переменные управления катастрофы сборки (а следовательно, и параметры проектирования) выступают как случайные величины, то в качестве метода поиска оптимального решения может быть использован один из методов случайного поиска – например, метод случайного поиска с уменьшением интервала.
Алгоритм поиска оптимального решения
Поиск оптимального решения при проектировании устройства защиты оператора может быть произведен в следующей последовательности:
1) этап постановки задачи: выбор целевой функции, ввод областных и функциональных ограничений, определение управляемых переменных;
2) оценка напряженно-деформированного состояния ROPS методом конечных элементов, построение уравнений линейной регрессии – зависимости жесткости ROPS от площади поперечного сечения профиля A1 = k1•S + k2;
3) оценка вероятности катастрофы сборки и выражение стоимости производства устройства защиты C1T и стоимости отказа C2T в зависимости от параметров управления;
4) построение целевой функции – суммарных затрат с учетом вероятности отказа (катастрофы сборки);
5) поиск оптимального решения – значений параметров управления, соответствующих минимуму целевой функции при заданных ограничениях методом случайного поиска с уменьшением интервала.
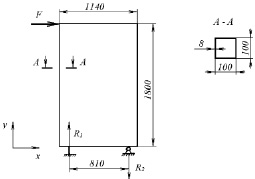
Схема ROPS ТЛК 4-01
Пример решения задачи оптимального проектирования rops трелевочного трактора ТЛК-4-01
Ввод исходных данных для оценки затрат на производство устройства защиты (сечение профиля – полый квадрат по ГОСТ 12336):
Fmin = 105 Н; R = 2,22 Fmin; l = 5,88 м; ρ = 7800 кг/м3;
С1 т м/п = 30000 руб./т; С1 т изг = 50000 руб/т;
C1 кг = (С1 т м/п + С1 т изг)/1000 = (30000 + 50000)/1000 = 80 руб./кг;
k = 2; С2T1 = 20000 руб; С2T2 = 0,5 С2T1; С2T3 = 0,5 С2T1; C2T4 = C1T.
Определение коэффициентов в уравнении регрессии A1 = k1•S + k2 производилось на основании величин жесткости A1, вычисленных с применением ППП «Зенит» для различных вариантов сечений профиля.
Оценка вероятности катастрофы сборки – по формуле (1), оценка стоимости производства устройства защиты C1T и стоимости отказа C2T в зависимости от параметров управления – по формулам (2)–(5).
Поиск оптимального решения осуществлен методом случайного поиска с уменьшением интервала, при этом наименьшему значению целевой функции соответствует жесткость системы ROPS A1 = 11510 Н/мм и площадь поперечного сечения квадратного профиля S = 3,191·103 мм2, которые наиболее близки к значениям, соответствующим квадратному профилю 110×110×8 с характеристиками A1 = 12020 Н/мм и S = 3,264·103 мм2.
Выводы
Базовый вариант ROPS в виде каркаса из стержней квадратного сечения 100×100×8, имеющий место на серийном колесном трелевочном тракторе «Онежец ТЛК 4-01», не является оптимальным вариантом конструкции. В свою очередь, наиболее близким к оптимальному является профиль с жесткостью A1 = 11510 Н/мм и площадью поперечного сечения S = 3191 мм2, что соответствует полому квадрату 110×110×8. Также рассмотрены такие варианты формы поперечного сечения стержней устройства защиты оператора, как полый прямоугольник, двутавр и швеллер. В случае прямоугольного сечения оптимальным является профиль с жесткостью A1 = 11080 Н/мм и площадью поперечного сечения S = 2160 мм2, что соответствует полому прямоугольнику 140×100×5; для двутавра – профиль с жесткостью A1 = 9003 Н/мм и площадью поперечного сечения S = 1524 мм2, что соответствует двутавру № 12 по ГОСТ 8239–89; для швеллера – профиль с жесткостью A1 = 10520 Н/мм и площадью поперечного сечения S = 1556 мм2, что соответствует швеллеру № 14 по ГОСТ 8240–89.
Работа выполнена при поддержке Программы стратегического развития (ПСР) Петрозаводского государственного университета в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.