При построении сетей предполагается, что входной и выходные слои заданы, то есть уже известно, что поступает на вход сети и что является ее выходом. То, какие переменные будут выходными, известно всегда (по крайней мере, в случае управляемого обучения). Однако сбалансировать входной набор данных весьма непросто. Чаще всего неизвестно заранее, какие из входных переменных действительно полезны, и выбор хорошего множества входов бывает затруднен целым рядом обстоятельств.
Каждый дополнительный входной элемент сети – это новая размерность в пространстве данных. С этой точки зрения, очевидно, что для того, чтобы иметь достаточную плотность точек и, как следствие, эффективно оценивать структуру данных, нужно иметь довольно много измерений (векторов данных).
Для осуществления контроля технического состояния авиационных двигателей, используется информация, поступающая от датчиков контролирующих параметров. Данная информация именуется как параметры полетного мониторинга, в силу того, что авиационный двигатель является конструктивно сложным элементом и производится контроль множества параметров, данные имеют большую размерность, порядка 40 атрибутов, что влечет за собой высокие требования к объему выборки данных, необходимой для обучения модели оценки технического состояния двигателя. Для того чтобы сократить размерность данных и исключить малозначащие и малоэффективные переменные, применяются следующие методы:
1. Корреляционный анализ [1] применяется для оценки зависимости выходных полей данных от входных факторов и устранения незначащих. Принцип подобного анализа состоит в поиске таких значений, которые в наименьшей степени коррелированы (взаимосвязаны) с выходным результатом. Такие факторы могут быть исключены из результирующего набора данных практически без потери полезной информации. Критерием принятия решения об исключении является порог значимости. Если корреляция (степень взаимозависимости) между входным и выходным факторами меньше порога значимости, то соответствующий фактор отбрасывается как незначащий.
Рассмотрим применение метода на данных по параметрам полетного мониторинга авиадвигателя. Для выполнения данного анализа было использовано специальное программное обеспечение (СПО) Deductor 5.3. На начальном этапе имеется набор данных размерностью 40 атрибутов, один из которых является целевым атрибутом (техническое состояние двигателя). Таким образом, можно составить почти 40 пар входной атрибут и целевой атрибут. Корреляция это число между – 1 и + 1, которое измеряет степень взаимосвязи между двумя атрибутами, применительно к текущей задаче можно оценить корреляцию между целевым атрибутом и одним каждый раз разным входным атрибутом. В табл. 1 показана интерпретация значений корреляции.
Таблица 1
Интерпретация корреляционных значений
|
Отрицательное значение |
Положительное значение |
Интерпретация |
|
– 0,2 < V < 0,2 |
Очень низкое значение |
|
|
– 0,5 < V < – 0,2 |
0,2 < V < 0,5 |
Слабая корреляция |
|
– 0,7 < V < – 0,5 |
0,5 < V < 0,7 |
Средняя корреляция |
|
– 0,9 < V < – 0,7 |
0,7 < V < 0,9 |
Высокое значение |
|
V < – 0,9 |
V > 0,9 |
Очень высокое значение |
На последующем этапе был выбран метод расчета корреляции – коэффициент корреляции Пирсона и рассчитаны значения функции корреляции (см. рис. 1) между каждым входным и выходным (техническое состояние двигателя) столбцами. На пересечении строки с именем входного поля и столбца с именем выходного поля находится значение рассчитанной между ними корреляции.
Исключение незначащих факторов производится на основании вычисленной корреляции путем задания необходимого уровня значимости. Столбцы, у которых максимальное из рассчитанных значений корреляции меньше порога, будут исключены из выходного набора.
Таким образом, согласно табл. 1, было установлено значение порога 0,5, тем самым были исключены входные столбцы (атрибуты), обладающие уровнем корреляции с целевым атрибутом (выходным атрибутом) ниже среднего. Следовательно, в ходе выполнения корреляционного анализа удалось исключить 15 малозначащих переменных.
2. Факторный анализ. В отличие от корреляционного анализа факторный анализ [4] учитывает взаимосвязь не только между двумя наборами данных (атрибутами). Цель факторного анализа заключается в понижении размерности пространства факторов. Это необходимо в случаях, когда входные факторы коррелированы друг с другом, т.е. взаимозависимы. В факторном анализе речь идет о выделении из множества измеряемых характеристик объекта новых факторов более адекватно отражающих свойства объекта.
Аналогично оценим эффективность метода на наборе данных полетного мониторинга в СПО Deductor 5.3. После выбора входных данных на анализ был определен метод факторного решения – метод ортогонального вращения Varimax (этот метод является наиболее часто применяемым, поскольку он облегчает интерпретацию факторов) и число выбираемых факторов – 25.
Для заданных переменных 25 рассчитаны главные компоненты. Таблица с результатами представлена на рис. 2.
Для того чтобы определить, какие главные компоненты необходимо включить в выходной набор, следует установить порог значимости, рекомендуемые значения которых выделены синим цветом. Регулируя данные значения, количество переменных, заданных на предыдущем шаге, может варьироваться. Последней по списку попадающей в выходной набор главной компонентой станет первая, у которой суммарный вклад в результат превысит порог значимости.
В ходе проведения факторного анализа из входного набора данных удалось выделить 25 главных компонент (факторов). Эффективность данного подхода определим на этапе моделирования классификатора.
Аналогичная задача по понижению размерности может быть выполнена с помощью нелинейных преобразований на базе автоассоциативных сетей (воспроизводят на выходе свои же данные). Число внутренних элементов данного рода сетей небольшое, что и заставляет сжимать данные. Типичная структура сети 5 слоев – средний слой сжимает, крайние выполняют нелинейные преобразования.
3. Анализ чувствительности. При моделировании нейронных сетей в СПО Statistical Neural Networks можно использовать различные комбинации входных переменных. Поэтому имеется возможность игнорировать некоторые переменные, так что полученная сеть не будет использовать их в качестве входов. Так же можно провести анализ чувствительности сети к входным переменным. Такая процедура позволяет сделать вывод об относительной важности входных переменных для конкретной нейронной сети и при необходимости удалить входы с низкими показателями чувствительности [2].
Используя набор данных полетного мониторинга, оценим эффективность анализа чувствительности. В ходе анализа поочередно будут исключаться входные переменные. Для того чтобы определить чувствительность каждой из переменных, сеть сначала обучается на тестовых значениях (т.е. на всем наборе данных, со всеми доступными переменными) и определяется ошибка N1 сети. Затем сеть обучается на тех же значениях, но в этот раз происходит «исключение» наблюдаемых значений с определением ошибки N2 сети.
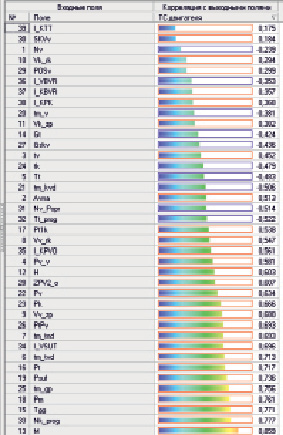
Рис. 1. Матрица корреляции
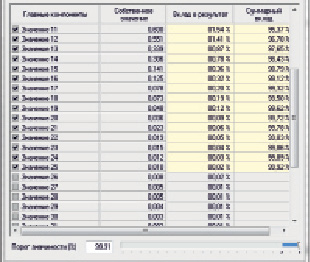
Рис. 2. Таблица со списком рассчитанных главных компонент
Таблица 2
Результаты анализа чувствительности
|
Ошибка |
Vv_zp |
Tv |
Pk |
Pt |
Tt |
Tm_v |
… |
|
|
Отношение 1 |
0,396 |
0,6785 |
0,6787 |
0,742 |
0,6792 |
1,004 |
… |
|
|
Ранг 1 |
19 |
16 |
13 |
15 |
3 |
… |
||
|
Отношение 2 |
0,273 |
0,989 |
0,961 |
1,0009 |
0,983 |
1,045 |
1,049 |
… |
|
Ранг 2 |
25 |
33 |
22 |
27 |
11 |
10 |
… |
|
|
Отношение 3 |
0,363 |
0,924 |
1,002 |
1,0074 |
1,0004 |
0,9994 |
… |
|
|
Ранг 3 |
25 |
13 |
11 |
14 |
17 |
… |
||
|
Отношение 4 |
0,144 |
0,944 |
1,013 |
1,0451 |
0,984 |
1,038 |
0,991 |
… |
|
Ранг 4 |
37 |
20 |
14 |
33 |
17 |
27 |
… |
Так как мы удалили некоторую информацию, которую использует сеть (т.е. одну из входных переменных), то резонно ожидать ухудшение ошибки. Значение чувствительности – это отношение ошибки N2 к исходной ошибке N1. Чем чувствительнее сеть к данному входу, тем большее ухудшение можно ожидать и, таким образом, тем больше отношение. Если отношение меньше либо равно 1, тогда отключение переменной не влияет на производительность сети. Полученные результаты показаны в табл. 2.
В ходе анализа было обучено 10 нейронных сетей типа многослойный персептрон, из них выбрано 4 с наименьшей ошибкой. Для каждой переменной рассчитано отношение ошибок и проставлен ранг. Как видно из таблицы, параметр Tt не участвовал в обучении 1 и 3 сетей, что негативно повлияло на ошибку, следовательно, можно сделать вывод о высокой значимости данной переменной. Так же анализируя таблицу, можно сделать предположение о том, что параметр VV_zp не является значимым и его можно исключить. Таким образом, был составлен набор данных из 27 переменных (атрибутов).
Для сравнительного анализа эффективности подходов было составлено три набора данных: набор после корреляционного анализа, набор после факторного анализа, набор после анализа чувствительности.
Таблица 3
Результаты моделирования при обучении на исходных данных
|
Наст. Неисправен |
Наст. Исправен |
|
|
Прогн. Неисправен |
19 |
4 |
|
Прогн. Исправен |
27 |
368 |
|
Отзыв класса |
41,30 % |
98,02 % |
|
Исходные данные. Точность классификации – 92,58 % |
||
Таблица 4
Результаты моделирования при обучении на данных после факторного и корреляционного анализа
|
Данные после факторного анализа. Точность классификации 91,39 % |
||
|
Наст. Неисправен |
Наст. Исправен |
|
|
Прогн. Неисправен |
25 |
15 |
|
Прогн. Исправен |
21 |
357 |
|
Отзыв класса |
54,35 % |
95,97 % |
|
Данные после корреляционного анализа. Точность классификации 91,39 % |
||
|
Прогн. Неисправен |
24 |
8 |
|
Прогн. Исправен |
22 |
364 |
|
Отзыв класса |
52,17 % |
97,85 % |
Таблица 5
Результаты моделирования при обучении на данных после анализа чувствительности
|
Наст. Неисправен |
Наст. Исправен |
|
|
Прогн. Неисправен |
10 |
51 |
|
Прогн. Исправен |
5 |
178 |
|
Отзыв класса |
66,66 % |
77,72 % |
Для того чтобы оценить эффективность и выявить наиболее результативный из подходов, необходимо осуществить проверку при моделировании классификатора. Сравнивая точности моделей, рассчитанных на основе данных матрицы ошибок, можно сделать вывод о пригодности и целесообразности использования определенного метода подготовки данных.
Итак, в качестве отправной точки нужно определить точность модели [5] на исходных данных, т.е. на данных без каких-либо манипуляций с атрибутами.
Из табл. 3 видно, что неисправные состояния двигателя распознаются с очень низкой точностью, это, несомненно, является проблемой.
Оценивая результаты после факторного и корреляционного анализа, видно, что повысилась точность распознавания неисправного состояния, но данный показатель до сих пор не является достаточно высоким для эффективного функционирования модели.
Точность классификации модели, обученной на данных после анализа чувствительности, составляет 77,04 %. Исключение некоторых атрибутов положительно повлияло на распознавание неисправного состояния двигателя, но в то же время значительно упала точность классификации модели в целом, в связи с тем, что точность определения класса «исправен» упала на 20 %.
Таким образом, применяя эти подходы по подготовке данных, была улучшена точность распознавания класса «неисправен» на 20 %, однако точность распознавания класса «исправен» упала на 20 %.
В данной статье был проведен сравнительный анализ методов подготовки данных к моделированию классификатора для оценки технического состояния авиадвигателя. Использованные методы целесообразно применять, особенно учитывая тот факт, что приоритет определения действительно существующей неисправности двигателя выше, чем ложное определение его неисправности. Следовательно, повышение точности распознавания неисправного класса оправдывается даже с учетом падения точности определения исправного класса. Оценивая ситуацию в целом, можно отметить, что модели не являются достаточно точными для выполнения поставленной задачи по классификации технического состояния авиационного двигателя. Причиной этого может быть значительный дисбаланс значений между классами, а именно недостаточное количество данных по классу «неисправен». Анализ данной проблемы описан в статье [3].
Библиографическая ссылка
Бочкарев С.В., Обухов Е.С. ОЦЕНКА МАТЕМАТИЧЕСКИХ МЕТОДОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ПОДГОТОВКИ ИСХОДНЫХ ДАННЫХ // Фундаментальные исследования. – 2016. – № 11-3. – С. 476-481;URL: https://fundamental-research.ru/ru/article/view?id=41001 (дата обращения: 20.04.2024).



