На современном этапе развития микропроцессорных систем электропривода переменного тока наибольший интерес для разработки и исследования представляют методики бездатчикового векторного управления асинхронным двигателем (АД). Построение таких систем позволяет не только устранить ряд проблем, присущих датчиковым системам, но и уменьшить стоимость электропривода и повысить его надежность. Для исключения датчика скорости или положения ротора используют специальные наблюдатели состояния, которые восстанавливают необходимые для управления координаты электропривода по доступным для измерения параметрам (токам, напряжениям, ЭДС статора).
Практическая реализация системы бездатчикового управления начинается с выбора методики управления и может решаться различными способами. Например, при использовании техники прямого управления моментом (DTC) [1, 3, 9] необходимо использование фильтров низких частот после датчиков тока, поскольку сам метод регулирования вызывает колебания вектора тока статора с частотой, пропорциональной несущей частоте векторной широтно-импульсной модуляции (ВШИМ). В целом на практике реализация управления с использованием DTC обладает рядом недостатков, вызванных неточностью вычисления производных, плохой спектральной картиной тока, а также значительными вычислениями, связанными с высоким порядком модели АД. Для устранения перечисленных недостатков предлагается выполнить построение системы управления с ориентацией вектора потокосцепления ротора по полю статора. Несмотря на то, что такие полеориентрированные системы считаются более сложными в настройке регуляторов и практической реализации математических преобразований [3], при использовании новейшей силовой электроники (IGBT) и микропроцессорной базы (DSP) они получили массовое применение в современных преобразовательных устройствах.
Рассмотрим структурную схему системы бездатчикового векторного управления с ориентацией по вектору потокосцепления ротора, которая представлена на рис. 1.
Для векторных систем управления с ориентацией по потокосцеплению ротора существуют различные методики вычисления скорости. Например, одни способы построения наблюдателей основаны на использовании матричного аппарата, с подстройкой коэффициентов матрицы наблюдаемости эталонной модели по вычисляемой невязке [1, 3], другие способы основаны на применении фильтра Калмана [5] или оценок ЭДС и потокосцепления ротора с использованием адаптивных моделей статора и ротора [2, 5, 6].
Рассмотрим практическую реализацию адаптивного наблюдателя с построением специальных моделей статора и ротора АД [1, 5]. Принцип работы предложенного наблюдателя скорости основан на вычислении невязки потокосцеплений опорной модели статора и адаптивной модели ротора. Для вычисления сигнала в среде MexBIOS Development Studio [10] разработан специальный блок (Complex Phase Difference) для математических операций в комплексных числах, определяющий разницу фаз с учетом квадранта, в котором находятся вращающиеся векторы тока в текущий момент времени [7]. Вычисленный таким образом сигнал невязки (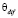 ) замыкается через регулятор на вход адаптивной модели ротора, что позволяет свести ошибку вычисления потокосцеплений моделей статора и ротора к нулю и определить тем самым действительную скорость ротора. Функциональная схема адаптивного наблюдателя показана на рис. 2.
) замыкается через регулятор на вход адаптивной модели ротора, что позволяет свести ошибку вычисления потокосцеплений моделей статора и ротора к нулю и определить тем самым действительную скорость ротора. Функциональная схема адаптивного наблюдателя показана на рис. 2.
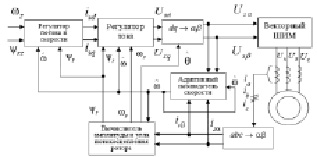
Рис. 1. Структурная схема бездатчиковой векторной системы управления
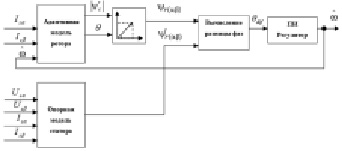
Рис. 2. Функциональная схема адаптивного наблюдателя
Синтез регулятора для наблюдателя скорости осуществляется с использованием стандартных настроек, с компенсацией наибольшей постоянной времени роторной цепи [1].
Составим опорную модель статора, для этого запишем векторные уравнения равновесия ЭДС статора и взаимосвязи потокосцеплений и токов статора и ротора для Т-образной схемы замещения [1, 5]:
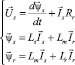 (1)
(1)
где Ls, Lr – полные индуктивности обмоток статора и ротора; Rs, Rr – сопротивления обмоток статора и ротора; Lm – взаимная индуктивность обмотки статора и ротора; 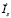 и
и 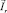 – обобщенные векторы тока статора и ротора;
– обобщенные векторы тока статора и ротора; 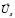 – обобщенный вектор напряжения статора;
– обобщенный вектор напряжения статора; 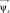 и
и 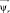 – обобщенные векторы потокосцепления статора и ротора.
– обобщенные векторы потокосцепления статора и ротора.
Из данной системы уравнений выразим векторы 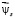 и
и 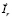 :
:
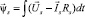 , (2)
, (2)
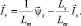 (3)
(3)
Подставим полученные выражения (2) и (3) в последнее уравнение системы (1) и определим вектор 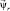 , который используется для построения адаптивной модели ротора:
, который используется для построения адаптивной модели ротора:
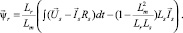 (4)
(4)
Полученное уравнение (4) непосредственно является моделью статора, которая отражает взаимосвязь токов и напряжений статора. Однако при практической реализации вычисления потокосцепления ротора по уравнению (4), возникает проблема связан с накоплением интегральных ошибок измерения токов и напряжений статора, что приводит к некорректному определению потокосцепления. Для решения обозначенной проблемы заменим блок интегрирования апериодическим звеном и перепишем уравнение (4) в проекциях на оси αβ [5]:
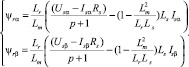 (5)
(5)
Система уравнений (5) позволяет вычислять потокосцепление ротора в проекциях на оси неподвижной системы координат (αβ) с использованием измерений напряжения и токов статора, что довольно просто решается в современных микропроцессорных преобразователях частоты.
Как уже было отмечено ранее, для построения адаптивного наблюдателя скорости одной опорной модели статора недостаточно, поэтому необходимо составить и реализовать адаптивную модель ротора.
Для решения этой задачи запишем систему уравнения равновесия ЭДС ротора и уравнения проекций потокосцеплений ротора на оси αβ 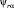 и
и 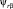 :
:
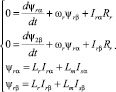 (6)
(6)
Подставим в уравнения равновесия ЭДС ротора проекции потокосцеплений ротора на оси αβ и получим «модель ротора» в виде следующей системы уравнений [2, 4]:
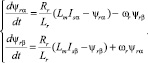 (7)
(7)
Структурная схема «моделей» статора и ротора, реализована в среде имитационного моделирования MexBIOS [10]. В качестве входных величин используются напряжения и токи статора в осях αβ.
Рассмотрим контур регулирования тока статора. На основании известного математического описания [1, 3] получен контур регулирования тока статора, структурная схема которого представлена на рис. 3.
Синтез регуляторов тока по осям d и q выполняем по известной методике с настройкой на технический оптимум [4, 8], в результате получен ПИ-регулятор с коэффициентами Ki и Kp.
Таким образом, в предложенной структуре (рис. 3), на выходе ПИ-регулятора тока, формируется управляющий вектор, который после компенсации нелинейностей и линейной коррекции, с учетом известных параметров модели АД должен сформировать заданный вектор тока на статорных обмотках.
В основе непосредственной коррекции электрического угла координатных преобразований заложен принцип формирования реальных статорных токов по задающему вектору 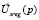 с помощью фазовой подстройки частоты. В более узком смысле коррекция угла необходима для более точной оценки потокосцепления ротора и работы адаптивной статорной модели, а также для исключения накопления интегральных ошибок при вычислении скорости [7].
с помощью фазовой подстройки частоты. В более узком смысле коррекция угла необходима для более точной оценки потокосцепления ротора и работы адаптивной статорной модели, а также для исключения накопления интегральных ошибок при вычислении скорости [7].
Структура системы бездатчикового управления с адаптивным наблюдателем скорости (рис. 1) была реализована в среде имитационного моделирования MexBIOS [10].
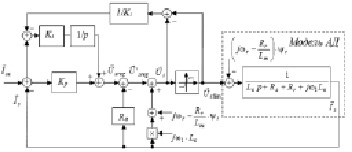
Рис. 3. Структурная схема контура регулирования тока статора
 а)
а) 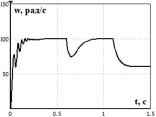 б)
б)
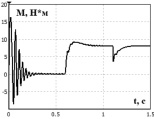
Рис. 4. Переходные процессы скорости (a) и момента (б)
 а)
а) 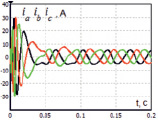 б)
б)
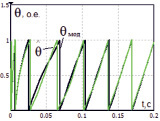
Рис. 5. Переходные процессы электрического угла (a) и токов статора (б) во время пуска
Для исследования работы системы управления при моделировании были выбраны следующие режимы:
- пуск двигателя без нагрузки с уставкой по скорости 100 рад/с (t =0 c);
- наброс нагрузки Мс = 8 Н·м (t =0,6 c);
- изменение уставки по скорости до 60 рад/с (t = 1,1 c).
Проанализировав полученные результаты переходных процессов (рис. 4 и рис. 5), можно сделать вывод, что все реализованные блоки выполняют расчеты корректно и бездатчиковая система управления функционирует в соответствии с заложенными критериями оптимизации. Результаты подтверждают эффективность предложенных подходов для разработки систем бездатчикового управления асинхронным двигателем. При этом следует учесть, что результаты имитационного моделирования были получены с учетом ряда допущений принятых при разработке моделей. Поэтому на следующем этапе проектирования бездатчикового управления необходима реализация системы на микропроцессорной платформе, с последующей оценкой ее работоспособности на лабораторном испытательном стенде.
Библиографическая ссылка
Даденков Д.А., Белоногов А.В., Варзаносов П.В. БЕЗДАТЧИКОВОЕ ВЕКТОРНОЕ УПРАВЛЕНИЕ С АДАПТИВНЫМ НАБЛЮДАТЕЛЕМ СКОРОСТИ И НЕПОСРЕДСТВЕННОЙ КОРРЕКЦИЕЙ ЭЛЕКТРИЧЕСКОГО УГЛА // Фундаментальные исследования. – 2016. – № 11-3. – С. 505-509;URL: https://fundamental-research.ru/ru/article/view?id=41006 (дата обращения: 24.04.2024).



