Современные следящие электроприводы (СЭП) обеспечивают очень высокие показатели качества отработки задающих и возмущающих воздействий, причем заявленное производителями время переходных процессов маломощных сервоприводов по контуру регулирования положения не превышает 20–60 мс, а полоса пропускания замкнутого контура регулирования положения уже достигает уровня 100–300 Гц.
При современном уровне развития теории оптимального и адаптивного управления, микропроцессорной и силовой полупроводниковой схемотехники контур регулирования момента является практически безынерционным и его, как правило, в задачах синтеза и анализа СЭП аппроксимируют простейшим апериодическим звеном первого порядка с ничтожно малой постоянной времени, не превышающей нескольких миллисекунд, а для маломощных сервоприводов – долей миллисекунд [13–15]. Однако доминирующую роль в формировании показателей качества технологических процессов с применением СЭП играют его фазовые переменные – скорость вращения и положение вала электродвигателя или линейные скорость и перемещение рабочего органа, что предполагает необходимость повышения быстродействия именно этих фазовых переменных. При этом традиционная архитектура СЭП не меняется уже несколько десятилетий, базируется на принципах подчиненного регулирования координат [1–5], и замкнутый контур регулирования положения включает в себя подчиненные контуры регулирования скорости и момента (тока).
Постановка задачи исследований
Для ограничения фазовых переменных в современных СЭП на входе замкнутых контуров регулирования положения и скорости устанавливают задатчики интенсивности первого или, что чаще, второго рода (S-рамп) и различные фильтры нижних частот, режекторные фильтры и др. [5, 13–15]. Это требует задания как минимум трех параметров S-рамп – величин допустимого ускорения и замедления, предельной скорости, величины предельно допустимого момента или механического рывка электропривода и времени их действия, а также постоянных времени фильтров или временных задержек изменения задающих сигналов. Это позволяет ограничить фазовые переменные СЭП на допустимых уровнях при изменении задания положения электропривода. Однако соподчиненность контуров регулирования положения, скорости и момента с включенными S-рампами и фильтрами на входах контуров приводит к ряду отрицательных последствий [2–5, 9]:
– неминуемое снижение быстродействия внешнего контура регулирования положения вследствие необходимости специфического распределения корней характеристических полиномов соподчиненных контуров в соответствии с фильтрами Баттерворта или аналогичными фильтрами низких частот, что принципиально не позволяет достичь предельного быстродействия отработки ошибок СЭП;
– обеспечение астатизма за счет введения интегральных компонент в структуры контурных регуляторов требует установки и параметрирования предшествующих фильтров для снижения перерегулирования или принятия специальных мер для исключения эффекта «накопленной ошибки», что дополнительно усложняет настройку микропроцессорных контроллеров СЭП, требует от наладчика детального изучения инструкций по наладке, знания тонкостей теории автоматического управления при вводе значений многочисленных параметров;
– включение инерционных звеньев (S-рамп и предшествующих фильтров) до компенсирующих позиционную и скоростную ошибки связей заведомо усугубляет условия для достижения хотя бы частичной инвариантности по отношению к задающим воздействиям.
Таким образом, анализ современного состояния СЭП позволил выделить три актуальных задачи исследований:
– разработка адаптивной к параметрам задающего воздействия эталонной модели (АЭМ), обеспечивающей формирование фазовых переменных СЭП (скорости, ускорения и рывка) с предельным быстродействием при заданных ограничениях;
– разработка процедуры синтеза регулятора положения и корректирующих звеньев для обеспечения частичной инвариантности СЭП и требуемого порядка астатизма по задающим воздействиям;
– имитационное моделирование разработанных СЭП для оценки таких показателей.
Рассмотрим обобщенную функциональную схему, содержащую две замкнутые обратными связями подсистемы (рис. 1).
1. Замкнутую подсистему адаптивной эталонной модели (АЭМ), включающую объект управления АЭМ – ОУ АЭМ, представляющий собой интегратор n-го порядка (для определенности в дальнейшем будем полагать, что n = 2), устройство управления АЭМ – УУ АЭМ, устройство вычисления периода управления – УВПУ.
2. Замкнутую подсистему собственно СЭП.
АЭМ включена на входе подсистемы СЭП и представляет собой адаптивный к параметрам внешней среды задатчик интенсивности того или иного порядка в зависимости от порядка интегратора АЭМ.
Обозначения переменных: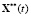 
– задающее воздействие внешней среды (в данном случае положения СЭП), 
; 
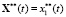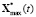– заданный вектор ограничений фазовых переменных СЭП, в общем случае допускающий изменения во времени; для АЭМ 2-го порядка
,
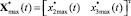где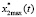 
, 
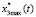– предельно допустимые значения скорости и ускорения электропривода, причем 
; 
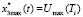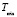– минимальное значение периода дискретного управления, определяющее полосу пропускания АЭМ в режиме малых отклонений переменных АЭМ и ограничивающее тем самым полосу пропускания разомкнутого тракта АЭМ – СЭП; 
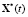– вектор фазовых переменных эталонной модели, 
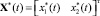; F(t) – вектор возмущений внешней среды, к основной компоненте которого относят изменение нагрузки на валу электропривода.
Вектор X(t) состояния СЭП содержит как минимум три компоненты: положение, скорость и электромагнитный момент (ток), но может содержать некоторый набор дополнительных переменных в зависимости от степени детализации элементов СЭП.
Будем полагать, что процессы в замкнутой АЭМ описываются дискретно-непрерывным уравнением:
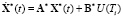, (1)
где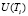 
– дискретное (цифровое) управление интеграторами эталонной модели,
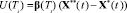, (2)
где Ti – период цифрового управления эталонной модели, изменяемый в некоторые i – моменты времени изменения задания внешней среды , i = 1, 2,… ,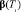 
– матрица искомых параметров управления АЭМ, зависящих от варьируемого периода Ti цифрового управления АЭМ, A* – матрица состояния АЭМ, 
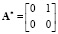, B* – матрица управления АЭМ, 
.
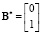Полагая, что АЭМ формирует оптимальные по быстродействию изменения выходной переменной, для нахождения неизвестных параметров матрицы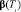 
воспользуемся теоремой об n интервалах цифровых финитных систем управления и методикой синтеза, детально рассмотренной в [6–8]. С учетом принятых моделей (1), (2) ниже представлены результаты синтеза для АЭМ второго порядка:
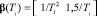, (3)
где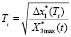 
– расчетное значение периода дискретного управления, 
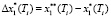– приращение задания выходной переменной АЭМ в некоторый заранее неизвестный i-й момент времени изменения задающего воздействия.
Обобщенная функциональная схема СЭП, соответствующая общепринятым структурам следящих электроприводов мировых производителей [5, 13–15], приведена на рис. 2.
Заметим, что при наличии АЭМ, формирующей вектор заданных фазовых переменных СЭП, корректирующие динамические звенья, обеспечивающие компенсацию позиционной и скоростной ошибки, становятся структурно проще. Несложно показать, что вместо дискретного ПДД-корректирующего звена достаточно применить два пропорциональных звена между выходами АЭМ по заданию скорости и ускорения и, соответственно, входами регуляторов скорости и момента. При этом СЭП отрабатывает эталонные задающие воздействия X*(t) сразу нескольких фазовых переменных. В общем случае (при n = 3) – это заданное положение рабочего органа и его три производных по времени – скорость, ускорение, рывок. При n = 2 задание рывка отсутствует.
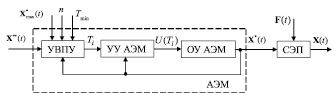
Рис. 1. Обобщенная функциональная схема СЭП с АЭМ
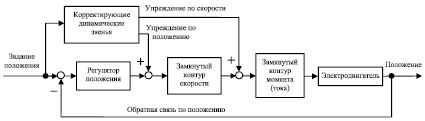
Рис. 2. Обобщенная функциональная схема СЭП
При использовании цифрового регулятора состояния в качестве регулятора положения ситуация аналогична, т.к. результат его синтеза дает равные коэффициенты по заданию и обратным связям [6, 10, 12], что эквивалентно одновременной отработке вектора ошибок слежения по координатам положения, скорости и ускорения. Именно это обстоятельство позволяет существенно увеличить добротности СЭП по скорости и ускорению, сводя динамическую установившуюся ошибку слежения при типовых степенных тестовых воздействиях практически к нулю. Разумеется, для того, чтобы обеспечить высокую добротность СЭП еще и по рывку, необходимо применить АЭМ как минимум 3-го порядка. Заметим, что регулятор состояния может быть синтезирован как для структуры с подчиненными контурами скорости и момента (тока), так и только с подчиненным контуром момента (тока).
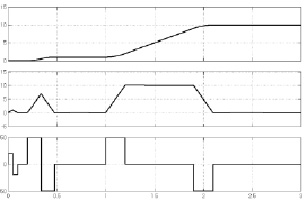
Рис. 3. Результаты моделирования процессов в АЭМ
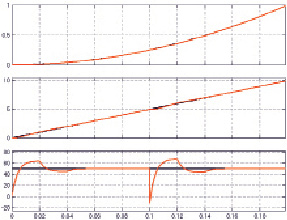
а)
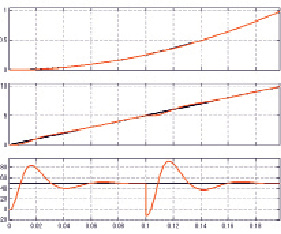
б)
Рис. 4. Результаты моделирования процессов в СЭП с типовой структурой (a) и с финитным регулятором состояния (б)
На рис. 3 приведены результаты моделирования переходных процессов в АЭМ. Приведены сформированные эталонной моделью сигналы задания трех фазовых переменных (сверху вниз) – положения, скорости и ускорения при следующих приращениях задающих воздействий на входе АЭМ: 0,05 рад при t = 0 с, 0,95 рад при t = 0,2 с и 9 рад при t = 1 с.
Заметим, что период дискретизации в АЭМ при формировании эталонных фазовых переменных СЭП меняется таким образом, что реализуется предельное быстродействие при заданных ограничениях фазовых переменных, а также формирование зоны линейной работы АЭМ заданием минимального значения Tmin. В этой зоне время переходного процесса неизменно, равно nTmin, а заданное ускорение не достигает допустимого ограничения.
На рис. 4, a приведены результаты моделирования переходных процессов по положению, скорости и ускорению (сверху вниз) в сквозном тракте АЭМ-СЭП при «постоянной заводке по ускорению» на уровне 50 рад/с2. Такт дискретного управления принят равным 0,001 с. В момент времени, равный 0,1 секунды, имитируется реакция СЭП на ступенчатое приложение к валу двигателя номинальной нагрузки.
На рис. 4, б приведены результаты моделирования переходных процессов в сквозном тракте АЭМ-СЭП с цифровым регулятором состояния (положение, скорость, ускорение) и подчиненным контуром регулирования тока якоря при тех же параметрах объекта управления и тестовых воздействиях, что и в предыдущем случае. Синтез регулятора состояния выполнен по критерию финитного управления [10, 12] за три интервала дискретного управления с постоянным периодом, равным 0,02 секунды.
Анализ результатов моделирования позволяет сделать следующие выводы:
– АЭМ формирует оптимальные по быстродействию задания фазовых переменных, причем ограничение ускорения на уровне 50 рад/с2 и ограничение сигнала дискретного управления АЭМ происходит только при достаточно больших приращениях задания положения, сформированных внешней средой (см. рис. 3);
– обе СЭП отрабатывают эталонное задание фазовых переменных с минимальной инерцией, практически дублируя задание (см. рис. 4, a–б);
– в СЭП с финитным регулятором состояния по сравнению с типовой СЭП добротность по ускорению в 4,3 раза выше и достигает уровня 6,5•105 с-2, а динамическая ошибка слежения – во столько же раз меньше при равных условиях моделирования и примерно равном времени переходных процессов (0,06 с).
Заключение
В результате проведенных исследований предложен новый подход к построению предельных по быстродействию и точности следящих электроприводов с адаптивными к параметрам задающих воздействий эталонными моделями. На основе предложенного подхода разработана оригинальная методика синтеза эталонных моделей, обеспечивающих оптимальность формирования до четырех фазовых переменных СЭП по критерию быстродействия с формированием переменного такта дискретного управления. При этом в эталонной модели реализуется возможность ограничения фазовых переменных на допустимых уровнях, что позволяет при синтезе регуляторов СЭП применить широкий арсенал методов линейной теории управления и упростить тем самым структуру и настройку системы управления. Результаты имитационного моделирования предложенных структур СЭП с АЭМ подтвердили эффективность предложенного подхода.
Библиографическая ссылка
Казанцев В.П., Лыков А.Н., Даденков Д.А. СЛЕДЯЩИЕ ЭЛЕКТРОПРИВОДЫ С АДАПТИВНЫМИ К ЗАДАЮЩИМ ВОЗДЕЙСТВИЯМ ЭТАЛОННЫМИ МОДЕЛЯМИ // Фундаментальные исследования. – 2016. – № 11-3. – С. 515-520;URL: https://fundamental-research.ru/ru/article/view?id=41008 (дата обращения: 23.11.2024).