В настоящее время появляется много инновационных проектов в различных областях науки, которые не всегда находят применение и реализацию в своем развитии.
Инновационный проект представляет собой сложную систему взаимообусловленных и взаимоувязанных по ресурсам, срокам и исполнителям мероприятий, направленных на достижение конкретных целей и задач на приоритетных направлениях развития науки и техники [3].
Целью данного исследования является определение «выживаемости» инновационных проектов. Под «выживаемостью» в данной работе понимается вероятность, с которой инновационный проект будет реализован.
Актуальность исследования обусловлена следующими факторами:
– большое количество инновационных проектов, представляемых в различных программах;
– необходимость определения характеристик «идеального» инновационного проекта, т.е. такого проекта, который точно будет реализован в дальнейшем.
К основным фазам жизненного цикла инновационного проекта относятся:
1. Предынвестиционная фаза – выполнение различных исследований для планирования инновационного проекта.
2. Инвестиционная фаза – составление документации по реализации инновационного проекта.
3. Фаза торгов и контрактов – на данной фазе заключаются контракты на поставку различного оборудования и выполнения работ.
4. Фаза реализации проекта – разработка планов и графиков выполнения работ по реализации проекта.
5. Завершающая фаза проекта – на данной фазе происходит закрытие инновационного проекта, запуск объекта в эксплуатацию и начало реализации товара, анализируются результаты работы.
В качестве исходных данных для оценки вероятности используются данные о проектах, участвующих в программах «УМНИК», «СТАРТ» и «УМНИК на СТАРТ», реализуемых Фондом содействия развитию малых форм предприятий в научно-технической сфере. Таким образом, «выживаемость» может быть определена как вероятность, с которой проекты пройдут все стадии в программах «УМНИК», «СТАРТ», «УМНИК на СТАРТ» и впоследствии станут успешно реализованы.
Программа «УМНИК» – это федеральная программа содействия развитию молодежных инновационных проектов [6]. В программе принимают участие только физические лица (программа ориентирована преимущественно на молодых специалистов, не имеющих опыта в предпринимательской деятельности).
Программа «СТАРТ» – это федеральная программа содействия развитию малых инновационных предприятий [4]. В программе принимают участие только юридические лица.
Программа «УМНИК на СТАРТ» – программа молодежных инновационных проектов, позволяющая победителям участвовать в программе «СТАРТ» [5]. В программе принимают участие победители программы «УМНИК», которые готовы создать малое инновационное предприятие для участия в программе «СТАРТ».
В ходе проведения данного магистерского исследования становится необходимым поиск метода определения «выживаемости» инновационных проектов. Были рассмотрены несколько методов, которые могут позволить адекватно оценить вероятность прохождения инновационными проектами всех стадий участия в федеральных программах («УМНИК», «СТАРТ», «УМНИК на СТАРТ») и дальнейшую реализацию.
Для определения «выживаемости» инновационных проектов рассмотрено несколько методов: исскуственные нейронные сети, генетические алгоритмы и Марковская модель.
Искусственная нейронная сеть – это система, состоящая из многих простых вычислительных элементов, работающих параллельно, функция которых определяется структурой сети, силой взаимных связей, а вычисления производятся в самих элементах или узлах [7].
Генетические алгоритмы – алгоритмы, предназначенные для решения задач оптимизации. Примером подобной задачи может служить обучение нейронной сети, то есть подбора таких значений весов, при которых достигается минимальная ошибка. При этом в основе генетического алгоритма лежит метод случайного поиска [1].
Случайный процесс в некоторой системе называется Марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние [2].
В результате исследования, для анализа «выживаемости» инновационных проектов, был выбран метод Марковских моделей, так как данный метод изначально учитывает Марковский характер жизненного цикла инновационного проекта.
Возникает проблема поиска неизвестных (скрытых) вероятностей перехода инновационных проектов по этапам участия в программах: «УМНИК», «СТАРТ» и «УМНИК на СТАРТ». Данная проблема решается с помощью подтипа Марковских процессов – скрытой Марковской моделью.
Скрытая Марковская модель – модель процесса, в которой процесс считается Марковским, причем неизвестно, в каком состоянии Si находится система (состояния скрыты), но каждое состояние Si может с некоторой вероятностью bioj произвести событие oj, которое можно наблюдать [2].
Обычно, при работе со скрытой Марковской моделью возникает несколько задач определения скрытых параметров. Для данного исследования воспользуемся задачей, которая определяет параметры модели λ = (P, O, π1), обеспечивающей максимальную вероятность P[O|λ], где P = [pi,j] – вероятность состояния перехода, O = [oj(m)] – вероятность наблюдений, π1 = (π1,i) – вероятность начального состояния.
Структура Марковской модели должна быть известна. Необходимо определить начальные вероятности каждого состояния и вероятности перехода между состояниями в данной модели. Для решения поставленной задачи применяется алгоритм Баума – Велша [8].
Алгоритм состоит из двух шагов. На первом шаге из известных параметров модели вероятность нахождения системы во время t в состоянии Si(γt(i)) и вероятность нахождение системы во время t в состоянии Si и во времени t + 1 в состоянии Sj данной последовательности наблюдений и модели (ξt(i, j)) вычисляется по формулам
ξt(i, j) = P(qt = Si, qt + 1 = Sj|O|λ),
γt(i) = Σ ξt(i, j),
где ξt(i, j) – вероятность нахождения во время t в состоянии Si и во время t + 1 в состоянии Sj для данной последовательности наблюдений и модели, γt(i) – вероятность нахождения во время t в состоянии Si.
На втором шаге модель λ вычисляется на основе значений γt(i), ξt(i, j).
Повторяем первый шаг с вычисленной λ. При многократном повторении этой процедуры вероятность совпадения вычисленной функции с исходной возрастает. Алгоритм сходится в тот момент, когда вероятность перестает изменяться.
В данном исследовании: набор состояний S = {S1, S2,…,SN} – состояния по программам; набор наблюдений V = {ν1, ν2,…, νM} – известные данные об инновационных проектах (количество инновационных проектов, количество заключенных контрактов и т.д.); модель λ = (P, O, π1).

Рис. 1. Этапы прохождения инновационным проектом стадий программ
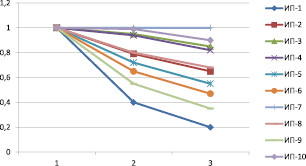
Рис. 2. Влияние критерия «Объем финансирования» на прохождение этапов инновационного проекта федеральных программ
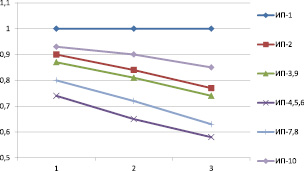
Рис. 3. Влияние критерия «Количество потенциальных заказчиков» на прохождение этапов инновационного проекта федеральных программ
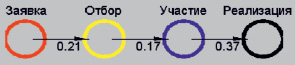
Рис. 4. Предсказанные, скрытые вероятности перехода инновационного проекта
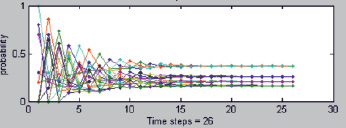
Рис. 5. Графическое представление итераций алгоритма Баума – Велша
Для исследования «выживаемости» инновационных проектов были выбраны необходимые данные по нескольким инновационным проектам из отчетов Фонда содействия развитию малых форм предприятий в научно-технической сфере за 2010–2013 гг.
Критериями, необходимыми для адекватного анализа «выживаемости» инновационных проектов, являются:
- Объем финансирования (т.р.).
- Окупаемость.
- Срок реализации.
- Количество статей по тематике.
- Количество потенциальных заказчиков.
Следующим шагом необходимо оценить влияние каждого критерия на этапы прохождения инновационным проектом стадий программ («УМНИК», «СТАРТ», УМНИК на СТАРТ»). Для более адекватной оценки влияния критериев объединим схожие этапы программ. В результате для оценки имеется три наиболее важных этапа (рис. 1).
На этапе оценки влияния каждого критерия инновационного проекта на стадии прохождения федеральных программ, наблюдается зависимость значения вероятности успешного прохождения какой-либо стадии программ от значения критерия. Для наглядности выведем графики критериев «Объем финансирования (т.р.)» (рис. 2) и «Количество потенциальных заказчиков» (рис. 3). На оси y отмечаются вероятности успешного прохождения стадии программ, а на оси x отмечаются стадии программ (1 – заявка, 2 – отбор, 3 – участие).
На завершающем этапе данного исследования необходимо практически реализовать алгоритм Баума – Велша и обучить скрытую Марковскую модель для предсказания вероятностей перехода какого-либо между стадиями федеральных программ («УМНИК», «СТАРТ», «УМНИК на СТАРТ»).
Обучение скрытой Марковской модели происходит с помощью алгоритма Баума – Велша и статистическими данными имеющейся выборки инновационных проектов в программном комплексе MATLAB.
Далее происходит получение данных о «новом», не входящем в статистическую выборку инновационном проекте. Данные об этом инновационном проекте загружаются в модель и происходит расчет скрытых вероятностей перехода (рис. 4). На рис. 5 наглядно представлен алгоритм Баума – Велша, который рассчитывает скрытые вероятности «нового» инновационного проекта и продолжает данные итерации до схождения.
В ходе выполнения итераций наблюдаем, что все параметры сходятся примерно на двадцатом шаге реализации алгоритма Баума-Велша.
Определение «выживаемости» позволит дать вероятностный прогноз относительно перспектив реализации инновационного проекта, также позволит оценить финансовые риски и другие показатели, связанные с их реализацией.
Библиографическая ссылка
Рашидов А.Р., Шмидт И.А. ОБЗОР МЕТОДОВ И РЕАЛИЗАЦИЯ АЛГОРИТМА СКРЫТОЙ МАРКОВСКОЙ МОДЕЛИ ДЛЯ АНАЛИЗА «ВЫЖИВАЕМОСТИ» ИННОВАЦИОННЫХ ПРОЕКТОВ // Фундаментальные исследования. – 2016. – № 11-3. – С. 588-592;URL: https://fundamental-research.ru/ru/article/view?id=41022 (дата обращения: 25.04.2024).



