На широкополосных станах горячей прокатки (ШСГП) при передаче крутящего момента от двигателя к рабочим валкам используют универсальные шпиндели (УШ) с бронзовыми вкладышами по ГОСТ 8059-83. В основу конструкции универсальных шпинделей положен принцип шарнира Гука (рисунок). Поэтому шпиндель с двумя шарнирами на его концах может передавать вращение и большие крутящие моменты от шестеренного валка к прокатному под углом наклона α = 8–10 °. При передаче крутящего момента Мкр в контактах вкладыша 1 с вилкой 2 и лопастью 3 возникают высокие контактные давления (рв и рл соответственно) и относительные перемещения вкладыша, сопровождаемые интенсивным износом поверхностей трения. При этом, как показывает практика, вкладыш в большей степени изнашивается в сопряжении с лопастью в периферийных точках, где действуют максимальные контактные давления рл = рл max. Их ресурс не превышает 1–1,2 месяца, а отказ шарниров приводит к остановке всего стана и снижению технико-экономических показателей, поэтому повышение ресурса является весьма актуальной задачей в теории и практике прокатного производства.
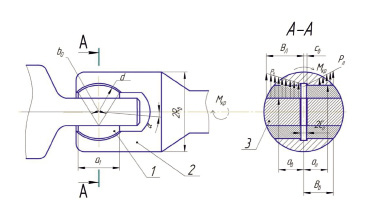
Расчетная схема шарнира универсального шпинделя
Несмотря на то, что момент отказа универсальных шпинделей на практике определяется по критерию износостойкости вкладыша (достижением его максимальным износом предельной величины), основными проектными расчетами, которые проводят на стадии конструкторской разработки, являются расчеты на статическую или циклическую прочность элементов вилки, лопасти и тела шпинделя по максимальным эквивалентным напряжениям [11, 3]. Аналитические методики расчета вкладышей на износ находятся в стадии разработки. В частности, в источниках [1, 12] предложена экспериментально-аналитическая методика расчета ресурса универсальных шарниров с использованием основной характеристики И.В. Крагельского [4] – линейной интенсивности изнашивания бронзового вкладыша Ih. Величину Ih определяют статистической обработкой большого объема экспериментальных данных, полученных в лабораторных испытаниях образцов или промышленных исследованиях шарниров.
Упомянутые методики построены на базовых положениях механики сплошной среды и не описывают реальные процессы повреждаемости и накопления дефектов атомно-молекулярной структуры материалов наиболее нагруженных элементов универсальных шпинделей. Основные определяемые параметры – максимальные напряжения при расчетах на прочность или интенсивность изнашивания Ih, не являются свойствами материалов, а характеризуют процесс нагружения элементов. Они изменяются в широких пределах и в зависимости от условий эксплуатации имеют крайне большое (более чем двух-, трехкратное) рассеяние. Поэтому в большинстве случаев модели не подтверждаются на практике без подбора соответствующих адаптационных коэффициентов [9].
Таким образом, практическое использование известных моделей при проектной оценке ресурса шарниров универсальных шпинделей требует либо проведения модельных испытаний образцов, либо специальных промышленных исследований, что существенно увеличивает затраты на стадии проектно-конструкторской разработки. Вопрос о чисто аналитической оценке показателей долговечности шарниров универсальных шпинделей в теории прокатного производства остается открытым.
Поэтому целью настоящих исследований является разработка аналитической модели отказов шарниров универсальных шпинделей по энергетическому критерию износостойкости бронзовых вкладышей на основе современных достижений теории надежности и кинетической концепции к описанию процессов повреждаемости и разрушения твердых тел.
Разработка модели износовых проектных отказов шарниров универсальных шпинделей
В основу построения модели положены базовые принципы общей концепции прогнозирования параметрической надежности технических объектов [6] и основные зависимости энерго-механической теории изнашивания стационарных трибосистем [2, 5]. Они получены совместным решением основополагающих уравнений молекулярно-механической [4] и структурно-энергетической [7, 8, 10] теорий трения. В этом случае в соответствии с правилами общей теории прогнозирования надежности узлов трения [2, 5] в качестве параметра  состояния шарнира принимаем величину среднего текущего износа вкладыша в наиболее нагруженных периферийных точках, где рл = рл max (рисунок). В процессе изнашивания вкладыша со средней скоростью
состояния шарнира принимаем величину среднего текущего износа вкладыша в наиболее нагруженных периферийных точках, где рл = рл max (рисунок). В процессе изнашивания вкладыша со средней скоростью  величина xt увеличивается от нуля до предельного значения xпр ≈ (0,01…0,03)•RB [12]. При этом будем полагать, что трибосопряжение работает в нормальных условиях эксплуатации при установившемся режиме фрикционного усталостного изнашивания. Износом лопасти можно пренебречь.
величина xt увеличивается от нуля до предельного значения xпр ≈ (0,01…0,03)•RB [12]. При этом будем полагать, что трибосопряжение работает в нормальных условиях эксплуатации при установившемся режиме фрикционного усталостного изнашивания. Износом лопасти можно пренебречь.
В таких условиях уравнение деградации (старения) шарнира в процессе будущей эксплуатации иусловие перехода его в предельное состояние можно записать в виде
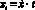 и
и 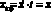 .
.
Решая последнее равенство относительно t = tпр, получим зависимость для расчета ожидаемого среднего ресурса шпинделя по критерию износостойкости вкладыша:
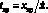 (1)
(1)
Для расчета скорости его изнашивания  используем базовую зависимость энерго-механической теории повреждаемости стационарных трибосопряжений вида [2]
используем базовую зависимость энерго-механической теории повреждаемости стационарных трибосопряжений вида [2]
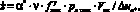 (2)
(2)
где α* – коэффициент перекрытия вкладыша;
v – коэффициент преобразования внешней энергии (работы сил трения) в материале поверхностного слоя вкладыша;
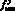 – механическая составляющая коэффициента трения в стационарном (установившемся) режиме;
– механическая составляющая коэффициента трения в стационарном (установившемся) режиме;
рл max – максимальное контактное давление в сопряжении вкладыша с лопастью (рисунок);
Vск – скорость скольжения периферийных точек поверхности трения вкладыша по поверхности лопасти;
 – критическая энергоемкость материала поверхностного слоя вкладыша.
– критическая энергоемкость материала поверхностного слоя вкладыша.
Для того чтобы незамкнутая система определяющих уравнений (1)–(2) оказалась статически определимой, необходимо сформулировать условия однозначности для определения параметров, входящих в эти зависимости. Условия однозначности включают отличительные признаки, начальные и граничные условия, выделяющие исследуемый объект (шарнир) из класса ему подобных. Отличительные признаки и расчетная схема фрикционного сопряжения шарнира представлена на рисунке.
Начальные условия, характеризующие состояние шарнира в момент времени t = 0, включают следующие группы задаваемых и рассчитываемых параметров.
Первая группа. Параметры внешнего нагружения (трения). Mкр, Vпр – крутящий момент и скорость прокатки.
Вторая группа. Геометрические характеристики вкладыша и лопасти (рисунок). а1 – ширина вкладыша; Вл – полуширина лопасти; α – угол наклона шпинделя; xпр – предельная величина износа вкладыша.
Третья группа. Микрогеометрические характеристики поверхностей вкладыша и лопасти. Ra(вкл), Ra(л) – среднеарифметическое отклонение профиля поверхностей; Δвкл, Δл – комплексные параметры шероховатости.
Четвертая группа. Физико-механические характеристики материалов вкладыша и лопасти. Евкл, Ел – модули упругости; μвкл, μл = 0,3 – коэффициенты Пуассона; σпц(вкл), σпц(л) – пределы пропорциональности; σТ(вкл), σТ(л) – пределы текучести; НВвкл, НВл – твердость по Бринеллю; НVвкл, НVл – твердость по Виккерсу; αГр(вкл), αГр(л) – коэффициенты гистерезисных потерь при растяжении, ρвкл, ρл – плотность материалов.
Пятая группа. Теплофизические характеристики материалов вкладыша и лопасти. λвкл, λл – коэффициенты теплопроводности; αвкл, αл – коэффициенты теплоотдачи; свкл, сл – удельная теплоемкость; ΔHS(вкл), ΔHS – энтальпия плавления;  ,
,  – исходная температура.
– исходная температура.
Шестая группа. Фрикционные характеристики сопряжения: τ0 – касательное напряжение межмолекулярного сцепления; β – коэффициент влияния нормального напряжения на коэффициент трения.
Граничные условия, характеризующие контактное взаимодействие элементов шарнира, должны включать следующие группы рассчитываемых параметров.
Первая группа. Параметры сопряжения.
Номинальная площадь контакта (Aa), площадь трения (AT) и коэффициент перекрытия α* вкладыша:
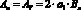 ;
; 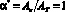 . (3)
. (3)
Максимальное удельное давление и максимальное значение средней скорости скольжения вкладыша по лопасти [1]:
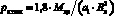 ;
;
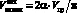 . (4)
. (4)
Вторая группа. Коэффициент трения.
Величина полного коэффициента трения fy и его механическая составляющая 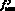 в установившемся режиме фрикционного взаимодействия определяется по известной методике Крагельского – Михина [4, 2] в зависимости от вида напряженного состояния поверхностного слоя вкладыша.
в установившемся режиме фрикционного взаимодействия определяется по известной методике Крагельского – Михина [4, 2] в зависимости от вида напряженного состояния поверхностного слоя вкладыша.
Третья группа. Температура вкладыша.
Температура поверхностного слоя вкладыша Tвкл в установившемся режиме трения определяется по известной методике А.В. Чичинадзе [9] в функции геометрических, кинематических, силовых параметров сопряжения и теплофизических характеристик материалов вкладыша и лопасти.
Четвертая группа. Энергетические характеристики.
Коэффициент преобразования внешней энергии (работы сил трения) поверхностным слоем материала вкладыша в изменение внутренней энергии поверхностного слоя вкладыша определяется по методике Б.В. Протасова [2]:
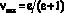 , (5)
, (5)
где ε – коэффициент распределения энергии между вкладышем и лопастью:
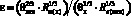 ; (5.а)
; (5.а)
θвкл, θл – упругие постоянные материалов вкладыша и лопасти:
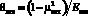 ;
; 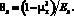 (5.б)
(5.б)
Плотность энергии дефектов структуры материала поверхностного слоя вкладыша в исходном состоянии [10]:
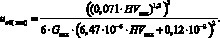 (6)
(6)
Энтальпия материала вкладыша при температуре Tвкл установившегося режима трения [10]:
 (7)
(7)
Критическая энергоемкость материала поверхностного слоя вкладыша [10]:
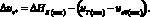 (8)
(8)
Совокупность уравнений (1)–(8) представляет модель износовых проектных отказов шарниров универсальных шпинделей по критерию износостойкости бронзовых вкладышей. На основе модели разработан алгоритм и программа «Долговечность УШ», позволяющая оценивать проектный ресурс tпр шарниров на стадии их конструирования в заданных условиях нагружения.
Адекватность теоретических результатов оценим сравнением значений, рассчитанных по предложенной методике, с данными, опубликованными в работах [1, 12].
Согласно [1, 12] расчетные (с использованием экспериментальной характеристики Ih) значения скорости изнашивания вкладышей из бронзы БрАЖ9-4 шарниров универсальных шпинделей привода валков первой чистовой клети стана 2000 Череповецкого металлургического завода составили:  мм/с – в работе [1];
мм/с – в работе [1]; 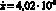 мм/с – в работе [12]. Расчет по предложенной выше методике показал, что
мм/с – в работе [12]. Расчет по предложенной выше методике показал, что 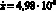 мм/с. Очевидно, что максимальное расхождение представленных результатов не превышает 20 %, что говорит о достаточной высокой достоверности теоретических разработок.
мм/с. Очевидно, что максимальное расхождение представленных результатов не превышает 20 %, что говорит о достаточной высокой достоверности теоретических разработок.
Заключение
Разработана математическая модель процесса формирования постепенных отказов шарниров универсальных шпинделей по критерию износостойкости бронзовых вкладышей.
На ее основе построены алгоритм и программа прогнозирования долговечности шарниров УШ приводов прокатных валков широкополосных станов, которые могут быть использованы:
– для расчета ожидаемого ресурса универсальных шпинделей различных прокатных станов на стадии проектно-конструкторской разработки или эксплуатации с опережением времени;
– проведения теоретических исследований по влиянию различных параметров на долговечность исследуемых шарниров и выбора наиболее долговечных вариантов конструкций без дополнительных экспериментальных исследований.
Библиографическая ссылка
Анцупов А.В. (мл), Анцупов А.В., Налимова М.В., Анцупов В.П., Русанов В.А. МОДЕЛЬ ОТКАЗОВ ШАРНИРОВ УНИВЕРСАЛЬНЫХ ШПИНДЕЛЕЙ ПО КРИТЕРИЮ ИЗНОСОСТОЙКОСТИ БРОНЗОВЫХ ВКЛАДЫШЕЙ // Фундаментальные исследования. – 2017. – № 4-1. – С. 9-12;URL: https://fundamental-research.ru/ru/article/view?id=41426 (дата обращения: 24.04.2024).



