В промышленности и сельском хозяйстве широко используются тонкоизмельченные порошкообразные материалы, диаметр частиц которых колеблется в пределах от 0,05 мм до 0,5 мм. Такие сыпучие материалы (например, каолин, технический углерод, белая сажа и др.) имеют малую насыпную плотность и высокую пористость, что приводит к увеличению затрат при их транспортировке, затаривании и хранении. Возникает необходимость принудительного уплотнения (деаэрации) порошков. Успех конструирования оборудования для этих целей и развитие методов расчета уплотнителей зависят от математического моделирования рассматриваемых процессов [1].
В работе [2] предложена классификация и анализ методов осуществления деаэрации тонкодисперсных материалов при упаковке продуктов. При этом показано, что пневматический метод, осуществляемый за счет газодинамических эффектов, является одним из наиболее эффективных методов. Широкое использование данного метода ограничено из-за его малой изученности и недостаточного математического описания [3].
При пневматическом (воздушном) уплотнении (рис. 1) более плотная упаковка твердых частиц происходит за счет сил атмосферного давления. Способ реализуется в емкости с непроницаемым дном при использовании вакуумной установки, создающей в пространстве вокруг порошка пониженное давление. По данным работы [4] пневматическая деаэрация при перепаде давлений порядка 8 кПа дает сокращение объема на 30–40 %.
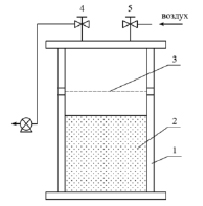
Рис. 1. Принципиальная схема пневматической деаэрации порошков: 1 – сосуд; 2 – порошок; 3 – фильтр; 4 и 5 – клапаны
Принцип действия пневматической деаэрации порошков состоит в следующем. В емкость 1 насыпается заданное количество порошка 2, с высотой слоя Н. Через клапан 4 медленно отсасывается воздух, благодаря чему в слое порошка создается пониженное давление с перепадом ΔР. При закрытом клапане 4 через клапан 5 происходит резкая подача атмосферного воздуха. За счет перепада давлений воздуха внутри и вне слоя порошка происходит его уплотнение.
На первом этапе математического моделирования рассмотрим процесс просачивания воздуха в слой порошка. Как и в работе [1], движение газообразной фазы будет описываться следующими уравнениями:
уравнение неразрывности газообразной фазы
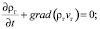 (1)
(1)
уравнение относительного движения газа в слое твердых частиц или закон Дарси
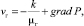 (2)
(2)
где μг – динамическая вязкость газа; k – коэффициент газопроницаемости, который зависит от пористости порошка и определяется выражением
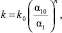 (3)
(3)
где n – некоторая константа; k0 – коэффициент газопроницаемости газа при начальной пористости α10;
уравнение состояния газа, которое для изотермического процесса записано в виде
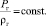 (4)
(4)
Система уравнений (1)–(4) может быть сведена к одному уравнению
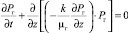 , (5)
, (5)
для которого начальные и граничные условия формулируются из следующих соображений. Дно емкости является абсолютно непроницаемым для газа, и относительная скорость движения газа равна нулю. В результате имеем
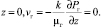 (6)
(6)
В начальный момент времени в слое газа одинаковое пониженное давление. Тогда
t = 0, Pг = Pa – ΔP, (7)
где ΔР – перепад давлений в слое порошка и вне его.
На поверхности слоя порошка давление газа равно атмосферному давлению. Математически это условие записывается в виде
z = h, Pг = Pa. (8)
Для удобства решения сделаем замену переменных
ΔPг = Pa – Pг. (9)
Тогда уравнение (5) с учетом условия
ΔPг << Pa (10)
можно привести к виду
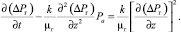 (11)
(11)
Начальные и граничные условия для уравнения (11) будут записываться в виде
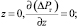 (12)
(12)
z = h, ΔPг = 0; (13)
t = 0, ΔPг = ΔP. (14)
Уравнение (11) с начальными и граничными условиями (12)–(14) решается численно сеточным методом с шагом hz по переменной z и с шагом ht по переменной t. Область решения представлена на рис. 2.
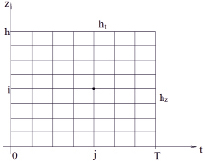
Рис. 2. Область решения задачи
Произвольной точке решения (i, j) соответствуют координаты
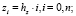 (15)
(15)
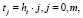 (16)
(16)
где параметры n и m определяются выражениями
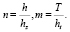 (17)
(17)
Значения производных в уравнении (11) заменим приближенными выражениями
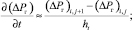 (18)
(18)
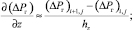 (19)
(19)
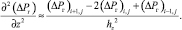 (20)
(20)
Подставляя выражения (18)–(20) в уравнение (11) и пренебрегая малыми членами, получим
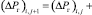
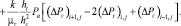 (21)
(21)
Исходя из начальных и граничных условий (12)–(14) в дополнение к выражению (21) получим
(ΔPг)0,j = (ΔPг)–1,j; (22)
(ΔPг)n,j = 0; (23)
(ΔPг)i,0 = ΔP. (24)
Уравнение (21) с условиями (22)–(24) решалось в среде Microsoft Visual Studio при следующих условиях: T = 10 с; h = 0,35 м; ΔP = 8·103 Па; k = 0,54·10-11 м2; μг = 0,182×10-4 Па·с; Pа = 105 Па; ht = 0,025 с; hz = 0,025 м. На рис. 3 приведены графики зависимости значения ΔPг от высоты слоя порошка при различных значениях времени, выполненные в среде Microsoft Excel.
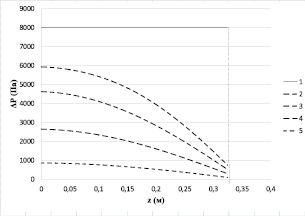
Рис. 3. Зависимость перепада давлений газа от высоты слоя порошка: 1 – t1 = 0 с; 2 – t2 = 0,5 с; 3 – t3 = 1 с; 4 – t4 = 2 с; 5 – t5 = 4 с
На втором этапе математического моделирования рассмотрим процесс непосредственно уплотнения порошка за счет перепада давлений в слое газа. При малых изменениях порозности порошка, как было показано в работе [1], твердый скелет испытывает упругие деформации, подчиняющиеся обобщенному закону Гука. Пренебрегая относительным движением слоев порошка, можно сделать предположение о равенстве напряжений, обусловленных упругими свойствами зернистого скелета, и напряжений, обусловленных избыточным давлением газа. Тогда в соответствии с данными работы [1] получим
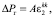 (25)
(25)
где А = (λ + 2μ)/3; ε2kk – первый инвариант тензора деформаций зернистого скелета, который определяется формулой [1]:
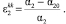 (26)
(26)
В выражениях (25), (26) λ, μ – коэффициенты Ламэ зернистого скелета; α2 – порозность порошка, связанная с пористостью порошка выражением
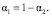 (27)
(27)
Согласно (25), (26), (27) после дифференцирования по времени (25) имеем
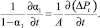 (28)
(28)
Следует отметить, что в уравнении (28) и пористость порошка α1 и избыточное давление газа ΔРг является функциями координаты z. При этом решение уравнения (21) позволяет рассчитывать величину ∂(ΔРг)/∂t для различных значений координат z и t.
Начальное условие для уравнения (28) записывается в виде
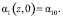 (29)
(29)
Уравнение (28) с начальным условием (29) решается численно сеточным методом, с шагом hz по переменной z и с шагом ht по переменной t. Переменные определяются по формулам (15), (16). Область решения соответствует области, представленной на рис. 2. При этом значение производной ∂(α1)/∂t в уравнении (28) заменим приближенным выражением
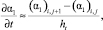 (30)
(30)
а значение производной ∂(ΔРг)/∂t заменим приближенным выражением (18).
Подставляя выражения (30), (18) в уравнение (28), получим
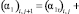
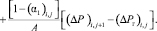 (31)
(31)
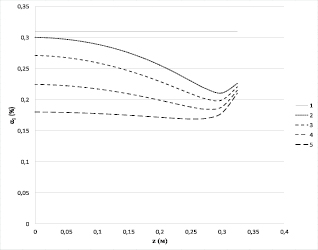
Рис. 4. Зависимость пористости порошка от высоты слоя порошка: 1 – t1 = 0 с; 2 – t2 = 0,5 с; 3 – t3 = 1 с; 4 – t4 = 2 с; 5 – t5 = 4 с
В соответствии c начальными и граничными условиями уравнение (31) должно быть дополнено условием
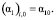 (32)
(32)
Уравнение (31) с условием (32) решалось в среде Microsoft Visual Studio при следующих условиях: T = 10 с; h = 0,35 м; λ = 38,7·103 Па; μ = 38,1·103 Па; ht = 0,025 с; hz = 0,025 м; α10 = 0,31. На рис. 4 приведены графики зависимости значения ΔPг от высоты слоя порошка при различных значениях времени, выполненные в среде Microsoft Excel.
Для проверки адекватности теоретических данных были проведены экспериментальные исследования по пневматическому уплотнению каолина (ГОСТ 16680-71) и технического углерода DF-100 (ГОСТ 7885-68), физико-механические свойства которых приведены в таблице. Общая схема экспериментальной установки соответствует схеме, представленной на рис. 1. Параметры порошков определялись по методикам, изложенным в работе [5].
На рис. 5 представлено сопоставление теоретических и экспериментальных данных по уплотнению порошков. Опыты проводились при одном и том же перепаде давлений ΔPг = 8 кПа. Степень уплотнения η определялась по коэффициентам уплотняемости [5], с учетом этого получим
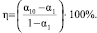 (33)
(33)
Результаты экспериментального определения характеристик порошков
|
№ опыта |
k·10-11 м2 |
α1 % |
λ·103 Па |
μ·103 Па |
ρн·103 кг/м3 |
h·10-2 м |
|
каолин (ГОСТ 16680-71) |
||||||
|
1 2 3 4 |
1,02 0,83 0,76 0,78 |
79 68 65 61 |
48,0 46,2 38,7 47,1 |
42,2 37,4 38,1 39,3 |
0,55 0,63 0,72 0,92 |
20,1 30,5 39,7 41,5 |
|
технический углерод DF-100 (ГОСТ 7885-68) |
||||||
|
1 2 3 |
0,75 0,62 0,48 |
79 76 65 |
7,6 5,3 4,8 |
9,3 7,7 6,7 |
0,37 0,41 0,44 |
45,2 51,3 64,5 |
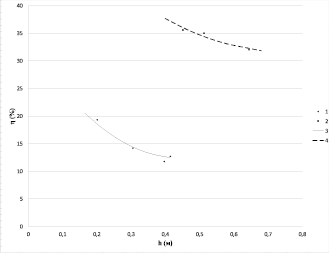
Рис. 5. Зависимость степени уплотнения порошка от высоты слоя порошка: 1, 3 – каолин (ГОСТ 16680-71); 2, 4 – технический углерод DF-100 (ГОСТ 7885-68)
Результаты проведенных экспериментов показывают, что при одном и том же давлении ΔPг = 8 кПа сокращение объема газа для технического углерода составило 33–39 %, а для каолина 12–21 %. Лучшие результаты уплотнения технического углерода по сравнению с каолином объясняются более низкой газопроницаемостью и сжимаемостью зернистого скелета. При этом экспериментальные данные удовлетворительно согласуются с расчетными данными. Максимальное расхождение не превышает 17 %.
Общий анализ приведенной математической модели пневматического уплотнения порошков показывает, что этот способ наиболее применим для порошков с низкой газопроницаемостью, не превышающей 0,8·10-11 м2, и низкой сопротивляемостью к сжиманию зернистого скелета, которая соответствует значениям коэффициентов Ламэ: λ< 8 кПа; μ < 10 кПа.
Библиографическая ссылка
Оборин А.В., Мурашов А.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПНЕВМАТИЧЕСКОГО УПЛОТНЕНИЯ ПОРОШКОВ // Фундаментальные исследования. – 2017. – № 8-2. – С. 292-297;URL: https://fundamental-research.ru/ru/article/view?id=41663 (дата обращения: 20.04.2024).



