Опыт показывает, что тела часто разрушаются квазихрупко, по определенным тонким поверхностям, области между которыми не разрушаются и не претерпевают заметных пластических деформаций. При расчетах на прочность с использованием компьютеров необходима предварительная дискретизация таких тел. Это часто осуществляют с использованием метода конечных элементов (МКЭ). Например, в работе [1] разработана математическая модель пространственного АЖКЭ, включающая в себя статические и геометрические ограничения, накладываемые АЖКЭ на напряженно-деформированное состояние упругих частей металлоконструкций. Описан алгоритм учета АЖКЭ применительно к МКЭ в форме метода перемещений. Приведены примеры расчетов, подтверждающие необходимость учета АЖКЭ с целью получения корректной матрицы жесткости. Метод АЖКЭ и обобщенных шарниров разрушения для общего случая деформирования пластин и оболочек разработан, в частности, авторами работ [2], для общего случая деформирования стержневых систем – авторами работы [3]. В работах [2, 3] использован кинематический метод теории предельного равновесия. Статический метод использован, в частности, в работах [4, 5]. Определение коэффициента запаса прочности по несущей способности осуществлено в работах [6, 7]. Задача определения несущей способности системы тонкостенная конструкция – грунт решена в работе [8]. В настоящей работе кинематический метод теории предельного равновесия развит применительно к массивным элементам конструкций (в том числе – к грунтовым массивам).
Тела, у которых все три измерения (длина, ширина, высота) – величины одного порядка, называются массивными [9]. Пусть такое тело нагружено внешними поверхностными pi и объемными γi силами:
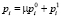 ,
, 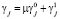 . (1)
. (1)
Здесь 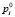 ,
, 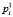 ,
, 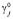 ,
, 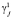 являются функциями только пространственных координат, μ – монотонно возрастающий параметр. Способ закрепления тела исключает возможность его перемещений и поворотов как целиком жесткого тела.
являются функциями только пространственных координат, μ – монотонно возрастающий параметр. Способ закрепления тела исключает возможность его перемещений и поворотов как целиком жесткого тела.
Необходимо определить предельное значение μ0 параметра внешнего нагружения, когда рассматриваемый массивный элемент теряет свойство геометрической неизменяемости.
В рассматриваемом случае, когда разрушение массивного тела происходит по отдельным «бесконечно» тонким обобщенным поверхностям разрушения (ОПР) между соседними АЖКЭ, основное энергетическое уравнение [10] можно записать в следующем виде:
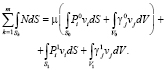 (2)
(2)
Здесь Sk – площадь k-й поверхности, по которой идет разрушение; m – число таких поверхностей; S0, S1 – площади на поверхности тела, где действуют силы 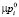 ,
, 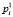 соответственно; V0, V1 – объемы в составе тела, где действуют силы
соответственно; V0, V1 – объемы в составе тела, где действуют силы 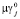 и
и 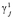 соответственно; N – мощность внутренних силовых факторов (ВСФ), приходящаяся на единицу площади; vi, vj – компоненты векторов скоростей движения точек тела, где приложены силы pi, γj соответственно.
соответственно; N – мощность внутренних силовых факторов (ВСФ), приходящаяся на единицу площади; vi, vj – компоненты векторов скоростей движения точек тела, где приложены силы pi, γj соответственно.
На рис. 1 изображены два соседних АЖКЭ P1B1…Bn и P2B1…Bn, контактирующие между собой через ОПР B1B2…Bn. Согласно теореме Шаля [11], движение каждого из АЖКЭ в трехмерном пространстве можно рассматривать как составленный из поступательного движения вместе с его полюсом и движения около полюса как неподвижного. Скорость диссипации внутренней энергии в произвольной точке Bi ОПР (рис. 1) определяется формулой
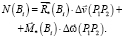 (3)
(3)
Здесь 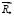 ,
, 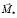 – главный вектор и главный момент внутренних распределенных сил, приведенных в точку Bi соответственно; они отнесены к единице площади;
– главный вектор и главный момент внутренних распределенных сил, приведенных в точку Bi соответственно; они отнесены к единице площади;

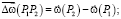 (4)
(4)
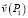 ,
, 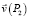 – скорости движения полюсов P1 и P2 (рис. 1) соответственно;
– скорости движения полюсов P1 и P2 (рис. 1) соответственно; 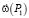 ,
, 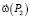 – мгновенные угловые скорости вращения соответствующих АЖКЭ около полюсов P1 и P2 соответственно.
– мгновенные угловые скорости вращения соответствующих АЖКЭ около полюсов P1 и P2 соответственно.
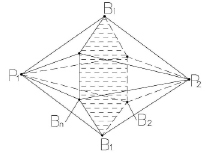
Рис. 1. Соседние АЖКЭ P1B1…Bn и P2B1…Bn
Равенство (3) имеет место, когда обобщение силы и скорости обобщённых перемещений связаны ассоциированным законом деформирования [10]
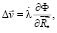
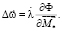 (5)
(5)
Здесь 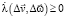 – скалярный множитель;
– скалярный множитель; 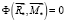 – уравнение предельной поверхности (поверхности прочности) в пространстве обобщенных сил. В соответствии с принципом максимума Мизеса имеем (рис. 1):
– уравнение предельной поверхности (поверхности прочности) в пространстве обобщенных сил. В соответствии с принципом максимума Мизеса имеем (рис. 1):
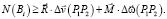 (6)
(6)
Здесь 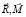 – любая комбинация обобщённых сил, удовлетворяющая условию
– любая комбинация обобщённых сил, удовлетворяющая условию 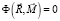 , но необязательно связанная ассоциированным законом деформирования с комбинацией
, но необязательно связанная ассоциированным законом деформирования с комбинацией 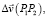
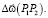
На рис. 2 изображён объемный элемент тела, имеющий единичные размеры, отнесенный к неподвижной системе координат XYZ. Внутренние силы, действующие на грани этого элемента, приведены в центры соответствующих граней. Главные векторы и главные моменты этих сил разложены по осям X, Y, Z. Получены векторы сосредоточенных сил 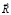 и сосредоточенных моментов
и сосредоточенных моментов 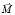 :
:
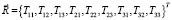 ;
;
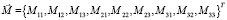 . (7)
. (7)
а) б)
Рис. 2. Объемный элемент тела
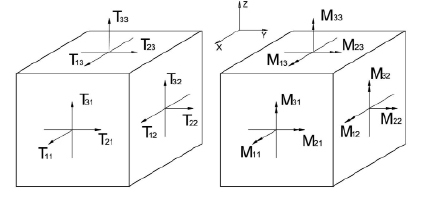
Представим рассматриваемую задачу в виде задачи математического программирования:
Найти min 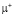 , где
, где
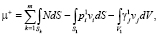 (8)
(8)
при интегральном ограничении
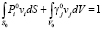 (9)
(9)
и при выполнении равенств вида (3) во всех точках всех ОПР. Для простоты записей некоторые знаки ∑ у интегралов в правых частях (2) и (8), а также в левой части (9) опущены.
Наиболее применяемым вариантом математического программирования является линейное программирование (ЛП). Представим задачу в виде задачи ЛП, которая решается с использованием симплекс-метода. Для этого интегрирование в (8) и (9) необходимо заменить суммированием конечных величин, а вместо (3) необходимо использовать систему ограничений вида (6), где различные комбинации 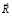 и
и 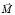 соответствуют вершинам выпуклого предельного многогранника, аппроксимирующего предельную поверхность
соответствуют вершинам выпуклого предельного многогранника, аппроксимирующего предельную поверхность 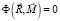 .
.
Внешние силы, приложенные в пределах отдельных АЖКЭ, можно привести к полюсам соответствующих АЖКЭ. В общем случае на рассматриваемой ОПР некоторые связи могут отсутствовать изначально. Тогда на ней соответствующие реакции (внутренние, или внешние) и их работа в процессе разрушения тождественно равны нулю.
Задача линейного программирования:
Найти min μ+, где
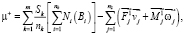 (10)
(10)
при ограничениях
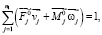 (11)
(11)
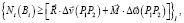 (12)
(12)
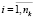 ,
, 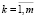 ,
, 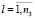 .
.
Здесь m – число ОПР; Sk – площадь k-й ОПР; nk – число точек на k-й ОПР, в которых определяется Ni(Bi); n1 – число АЖКЭ, к которым приложены внешние активные силы, зависящие от μ; n2 – число АЖКЭ, к которым приложены силы, не зависящие от μ; n3 – число вершин предельного многогранника в пространстве ВСФ; 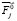 ,
, 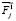 ,
, 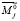 ,
, 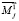 – силы и моменты, полученные в результате приведения внешних сил, действующих на j-й АЖКЭ, к его полюсу;
– силы и моменты, полученные в результате приведения внешних сил, действующих на j-й АЖКЭ, к его полюсу; 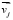 ,
, 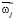 – скорости перемещения полюса j-го АЖКЭ и его поворота вокруг своего полюса, соответственно;
– скорости перемещения полюса j-го АЖКЭ и его поворота вокруг своего полюса, соответственно; 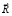 и
и 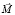 в (12) определяют произвольную вершину предельного многогранника;
в (12) определяют произвольную вершину предельного многогранника; 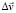 ,
, 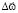 определяются в каждой точке Bi. Число ограничений вида (12) равно произведению числа всех точек Bi на число вершин предельного многоугольника (в случае однородных тел предельный многогранник может быть одинаковым для всех точек Bi). Согласно (10) N на Sk определяется как сумма объемов прямоугольных призм с одинаковыми площадями оснований. Возможны другие варианты аппроксимации N в пределах Sk (например, суммой объемов непрямоугольных призм с различными треугольными основаниями и т.д.). Соотношения (10), (11), (12) переписаны нами в проекциях на оси неподвижной системы координат XYZ. Задачи ЛП, Ni ≥ 0 являются несвободными переменными задачи ЛП,
определяются в каждой точке Bi. Число ограничений вида (12) равно произведению числа всех точек Bi на число вершин предельного многоугольника (в случае однородных тел предельный многогранник может быть одинаковым для всех точек Bi). Согласно (10) N на Sk определяется как сумма объемов прямоугольных призм с одинаковыми площадями оснований. Возможны другие варианты аппроксимации N в пределах Sk (например, суммой объемов непрямоугольных призм с различными треугольными основаниями и т.д.). Соотношения (10), (11), (12) переписаны нами в проекциях на оси неподвижной системы координат XYZ. Задачи ЛП, Ni ≥ 0 являются несвободными переменными задачи ЛП, 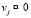 ,
, 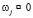 – свободными переменными. Составлена программа для ЭВМ в среде Matlab. Ниже приведены некоторые результаты расчетов, полученные с использованием этой программы.
– свободными переменными. Составлена программа для ЭВМ в среде Matlab. Ниже приведены некоторые результаты расчетов, полученные с использованием этой программы.
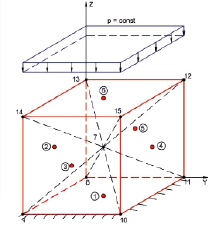
На рис. 3, а изображен куб с размерами 1x1x1 (м) из однородного изотропного материала. На верхнюю грань куба действует равномерное давление с интенсивностью 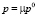 . Нижняя грань куба жестко защемлена. Необходимо определить предельное значение μ0 параметра внешней нагрузки.
. Нижняя грань куба жестко защемлена. Необходимо определить предельное значение μ0 параметра внешней нагрузки.
На рис. 3, а, куб разбит на 6 одинаковых АЖКЭ в форме пирамид; полюса АЖКЭ совпадают с центрами соответствующих граней куба, их номера указаны в кружочках. От 7 до 15 пронумерованы так называемые «сложные точки разрушения»; например, в точке № 7 сходятся 12 ОПР, соответственно, там будут 12 так называемых «простых точек разрушения», в каждой из которых должны выполняться ограничения вида (12). По условиям задачи АЖКЭ № 1 неподвижен. Вершины предельного многоугольника в пространстве ВСФ (7) имеют следующие координаты: 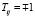 (MH/м2),
(MH/м2), 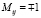 (MH/м2),
(MH/м2),  .
.
Для варианта дискретизации на рис. 3, а получены следующие результаты решения рассматриваемой задачи: μ+ = 1,414 MH•м/с; vz(2) = vz(3) = vz(4) = vz(5) = vz(6) = – 1 м/с; остальные компоненты 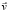 и
и  для всех АЖКЭ равны нулю. Скорость диссипации внутренней энергии N имеет постоянное значение, равное 1 MH/(м•с), на четырех ОПР 7-8-9, 7-9-10, 7-10-11, 7-11-8, т.е. процесс разрушения идет по этим плоскостям.
для всех АЖКЭ равны нулю. Скорость диссипации внутренней энергии N имеет постоянное значение, равное 1 MH/(м•с), на четырех ОПР 7-8-9, 7-9-10, 7-10-11, 7-11-8, т.е. процесс разрушения идет по этим плоскостям.
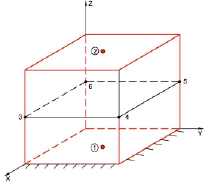
На рис. 3, б рассматриваемый куб разбит только на 2 АЖКЭ плоскостью, параллельной координатной плоскости OXY. Остальные условия задачи – прежние, т.е. упрощающие предположения в отношении, например, степеней свободы АЖКЭ, количества вершин предельного многогранника (их число по-прежнему равно 36) не приняты. Для этого варианта дискретизации куба получены следующие результаты: μ+ = 1 MH•(м/с); vz(2) = – 1, остальные составляющие 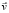 и
и 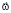 для всех АЖКЭ равны нулю; скорость диссипации N = 1 MH/(м•с) на ОПР 3-4-5-6. Процесс разрушения идет по этой плоскости в результате исчерпания прочности материала куба на сжатие.
для всех АЖКЭ равны нулю; скорость диссипации N = 1 MH/(м•с) на ОПР 3-4-5-6. Процесс разрушения идет по этой плоскости в результате исчерпания прочности материала куба на сжатие.
а) б)
Рис. 3. Куб с размерами 1x1x1 (м) из однородного изотропного материала
Как видно из приведенных результатов решения рассматриваемого примера, дискретизация куба согласно рис. 3, а дает значение μ+, завышенное на 41,4 % (кинематический метод дает верхнюю оценку разрушающей нагрузки [9]), а дискретизация согласно 3, б, позволяет получить точное значение μ+ = μ0 = 1 MH•м/с. При дискретизации не нужно стремиться к разбиению конструкции на большое число АЖКЭ, а нужно постараться, при минимально необходимом количестве АЖКЭ, «уловить» истинную картину разрушения.
Нами были исследованы и другие варианты нагружения рассматриваемого куба (например, различные сочетания вертикальной и горизонтальной нагрузок). Полученные результаты (которые здесь не приведены) также соответствуют, на наш взгляд, действительной картине разрушения.
Библиографическая ссылка
Сибгатуллин Э.С., Сибгатуллин К.Э., Новоселов О.Г. МЕТОД ОПРЕДЕЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ МАССИВНЫХ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ // Фундаментальные исследования. – 2017. – № 10-1. – С. 51-55;URL: https://fundamental-research.ru/ru/article/view?id=41788 (дата обращения: 19.04.2024).



