Известно [1], что эффективность термоэлектрического преобразования энергии существенно зависит от двух факторов. Во-первых, для тепловой машины, которой является термоэлектрогенератор, необходима максимально возможная разность температур горячей и холодной поверхностей, что, в свою очередь, определяется источником тепла. Во-вторых, необходимы высокие значения, так называемой термоэлектрической добротности, которую обычно обозначают произведением ZT и в существо которой в данной статье не будем углубляться. Именно в направлении повышения термоэлектрической добротности термоэлектроматериалов в настоящее время концентрируются исследования и разработки в области термоэлектрических генераторов.
Таким образом, одной из основных задач современной энергетики является преобразование тепловой энергии в электрическую. А одним из основных направлений реализации этой задачи является повышение термоэлектрической добротности полупроводниковых материалов, применяемых для создания термоэлектрогенераторов.
В настоящее время термоэлектрические генераторы с высоким КПД создаются на основе Bi2Te3 – для низких температур, PbTe – для средних температур и Ge-Si – для высоких температур [2–4].
Следует отметить, что в настоящее время не существует термоэлектрическихх материалов, которые бы в полной мере удовлетворяли как разработчиков и производителей, так и потребителей своими характеристиками. При этом какие-либо принципиальные ограничения на величину термоэлектрической добротности пока неизвестны, поэтому поиск материалов с лучшими свойствами должен продолжаться. Существенными инструментами в создании новых материалов для термоэлектрогенераторов являются эксперимент и моделирование.
Можно выделить три основных метода повышения термоэлектрической эффективности материала: 1) легирование халькогенидами или металлами, образующими твердые растворы; 2) добавление наноразмерных частиц в исходную матрицу; 3) использование дисперсных материалов. Как известно, повышение термоэлектрической добротности связано с изменениями фононной (решеточной) и электронной составляющих теплопроводности материала и изменением при этом электропроводности.
Добавление в матрицу основного материала термоэлектрогенератора микро- и наночастиц увеличивает дефектность структуры материала путем образования поверхностей раздела матрица – частица примеси. На этих поверхностях испытывают дополнительное рассеяние тепловой поток и электрический ток, что приводит к изменению коэффициентов тепло- и электропроводности материала. Можно считать, что изменение теплопроводности и электропроводности происходит пропорционально площади поверхности раздела фаз. Поэтому можно ожидать, что увеличение площади межфазной границы приведет к повышению термоэлектрической добротности такого композиционного материала. Кроме того, из-за сегрегации [5] и образования химических соединений [6] на межфазной поверхности разнородных материалов будут изменяться электрофизические и теплофизические свойства этой поверхности, что, в свою очередь, может оказать значительное влияние на термоэлектрическую добротность материала термоэлектрогенератора.
Повышение термоэлектрической добротности возможно также увеличением дисперсности, то есть путем уменьшения размера зерен в процессе кристаллизации термоэлектрического материала. На практике для изготовления термоэлектрических элементов часто используют спрессованные мелкодисперсные материалы [7]. Однако более перспективным является получение мелкодисперсного материала в процессе быстрой кристаллизации, то есть при высоких скоростях охлаждения при кристаллизации или путем иных внешних воздействий. Одним из возможных вариантов получения мелкодисперсного материала является кристаллизация расплава в поле высокочастотных акустических колебаний, причем, на наш взгляд, длины волн воздействующего ультразвука при этом должны быть близкими к длинам волн акустической эмиссии в процессе кристаллизации. В этом случае, при наложении упругих волн кристаллизации и внешних механических колебаний с той же величиной длин волн, можно ожидать наибольшего искажения кристаллической решетки в поцессе кристаллизации материала термоэлектрогенератора, что в свою очередь, должно привести к увеличению дисперсности закристаллизованного материала.
На рис. 1 представлены на примере олова экспериментальные данные зависимости средней площади поверхности кристаллических зерен от частоты ультразвука, полученные нами при акустическом воздействии на расплав в процессе его кристаллизации.
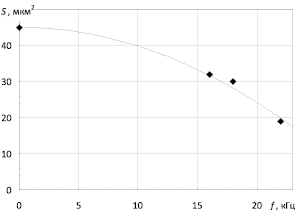
Рис. 1. Зависимость средней площади поверхности зерен олова от частоты ультразвукового воздействия при фазовом переходе из жидкого состояния в твердое (нулевая частота соответствует отсутствию ультразвукового воздействия)
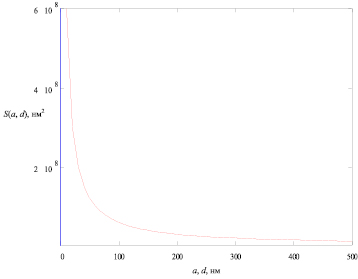
Рис. 2. Зависимость суммарной площади S(а, d) поверхности зерен 1 мкм3 (109 нм3) однофазного материала от размера грани а кубических или диаметра d сферических зерен
При одних и тех же условиях кристаллизации, то есть при одинаковой скорости охлаждения, были получены образцы, закристаллизованные без внешнего воздействия (0 кГц на графике) и при непосредственном воздействии акустическими волнами с частотами 16, 18 и 22 кГц. Как видно из рисунка, с повышением частоты ультразвукового воздействия от 16 до 22 кГц средний размер зерен уменьшается более чем на 40 %. В этой области частот изучаемая зависимость для олова при условиях эксперимента может аппроксимироваться линейным уравнением
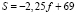 ,
,
где S – средняя площадь поверхности зерен, выраженная в квадратных микрометрах, а f – частота воздействующего ультразвука, выраженная в килогерцах. При этом дисперсный анализ (анализ зависимости числа зерен от площади их поверхности) показал Гауссово распределение.
Рассмотрим наноразмерные частицы двух простых геометрических форм: кубической и сферической одного и того же объема V. Зависимость площади поверности раздела включений в однородную матрицу определяется для кубика и сферы соответственно соотношениями
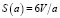 и
и 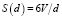 ,
,
где S – площадь поверхности, а а и d – ребро куба и диаметр сферы соответственно. Таким образом, эти зависимости являются идентичными. Тогда зависимость суммарной площади поверхности кубических и сферических зерен в 1 мкм3 (109 нм3) будет выглядеть, как представлено на рис. 2.
Если разместить на поверхности зерен углеродные наночастицы, например такие, как фуллерен С60, то их концентрация будет зависеть от суммарной площади поверхности зерен. С увеличением размера зерен их концентрация уменьшается. Эта зависимость определяется соотношением
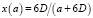 ,
,
где D = 0,71 нм – диаметр фуллерена С60. Эта зависимость (рис. 3) имеет гиперболический характер, и, как видно из рисука, значимое изменение концентрации частиц наблюдается при размерах зерен до 100 нм.
Площадь поверхности раздела фаз существенно зависит от геометрической формы частиц включений. Результаты расчета зависимости суммарной площади межфазной поверхности двухфазного композиционного материала от концентрации и размера частиц в 1 мкм3 для кубической и сферической формы частиц представлены на рис. 4, а для одно-, двух-, трех-, четырех- и пятислойных углеродных нанотрубок диаметрами 1,37; 2,01; 2,69; 3,37 и 4,05 нм соответственно – на рис. 5.
Как видно из рисунков, площади межфазной поверхности частиц кубической и сферической форм отличаются от соттветствующей площади для углеродных нанотрубок на несколько порядков величины. С увеличением диаметра (числа слоев) нанотрубок от 1,37 до 4,05 нм суммарная площадь уменьшается в несколько раз.
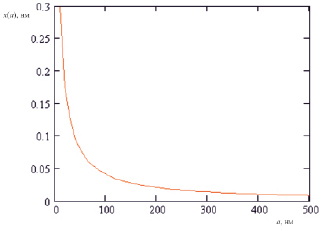
Рис. 3. Зависимость концентрации x(a), выраженной в относительных долях, фуллеренов в 1 мкм3, размещенных однослойно на поверхности зерен от размера a зерен кубической или сферической формы
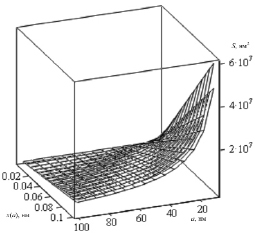
Рис. 4. Зависимость суммарной площади межфазной поверхности S (нм2) от концентрации x (относительные доли) и размера a (нм) частиц кубической и сферической формы в 1 мкм3 двухфазного композиционного материала
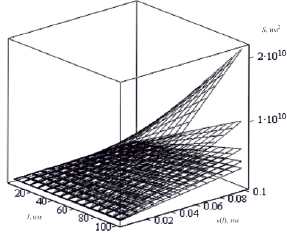
Рис. 5. Зависимость суммарной площади межфазной поверхности S (нм2) в 1 мкм3 двухфазного композиционного материала от концентрации x (относительные доли) и длины l (нм) одно-, двух-, трех-, четырех- и пятислойных углеродных нанотрубок диаметрами 1,37; 2,01; 2,69; 3,37 и 4,05 нм соответственно (сверху вниз)
Таким образом, форма и размеры частиц оказывают существенное влияние на суммарную площадь при размерах частиц менее 100 нм. В этих случаях свойства межфазной границы будут оказывать существенное влияние на физические, в частности электрофизические и теплофизические, свойства наноматериалов, что оказывается существенным с точки зрения разработки материалов для термоэлектрогенераторов.
Библиографическая ссылка
Кармоков А.М., Молоканова О.О., Молоканов О.А., Калмыков Р.М. ЗАВИСИМОСТЬ ПЛОЩАДИ МЕЖФАЗНОЙ ПОВЕРХНОСТИ В ПОЛИКРИСТАЛЛАХ И КОМПОЗИЦИОННЫХ МАТЕРИАЛАХ ОТ КОНЦЕНТРАЦИИ И ГЕОМЕТРИИ НАНОЧАСТИЦ // Фундаментальные исследования. – 2017. – № 10-3. – С. 449-453;URL: https://fundamental-research.ru/ru/article/view?id=41856 (дата обращения: 25.04.2024).



