Нахождение оптимального алгоритма, т.е. такого, при выполнении которого потребуется наименьшее количество арифметических действий или наименьшее машинное время, является одной из актуальных проблем теории алгоритмов. Практически во всех наиболее часто используемых математических моделях природных явлений так или иначе используются дифференциальные уравнения. Поэтому поиск таких алгоритмов, которые позволяют аппроксимировать решения задач теории дифференциальных уравнений за счет выполнения наименьшего количества арифметических действий, является актуальной проблемой [1, с. 6–7].
Целью данной статьи является использование цепных дробей в качестве аппарата приближения [2].
I. Рассмотрим:
1. Общее уравнение Д. Риккати
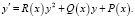(1)
2. Линейное уравнение второго порядка
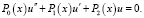(2)
3. Систему дифференциальных уравнений
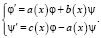(3)
В (1)–(3) R, Q, P, P0, P1, P2, a, b, c – известные, непрерывные на некотором отрезке [a, b], функции;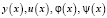 
– неизвестные функции [3].
Между решениями уравнений (1)–(3) существует связь, устанавливаемая следующими утверждениями.
Теорема 1. Если y – решение уравнения (1), то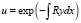 
будет решением уравнения (2).
Доказательство. Так как
, 
,
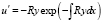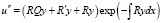то
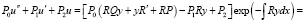
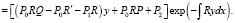
Последнее выражение равно нулю если подобрать P0, P1, P2 так, чтобы
, 
.
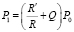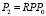Теорема 2. Если u – решение уравнения (2), то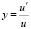 
будет решением уравнения (1).
Доказательство. Имеем
.
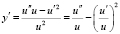Поэтому
.
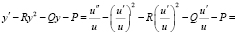
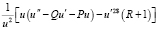Последнее выражение равно нулю, если подобрать R, Q, P из условий
R = –1,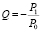 
, 
.
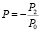Теорема 3. Если пара (φ, ψ) – решение системы (3), то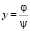 
будет решением уравнения (1).
Доказательство. Имеем
,
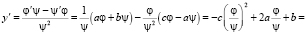
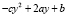т.е. y есть решение уравнения (1), где R = –c, Q = 2a, P = b.
Теорема 4. Если y – решение уравнения (1) и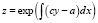 
, то пара 
, 
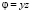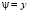будет решением системы (3).
Доказательство. Имеем
, 
.
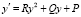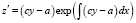Так как
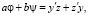
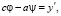
то
,
.
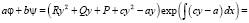
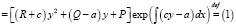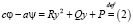Решая последнюю систему уравнений относительно φ и ψ, получим
,
.
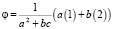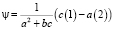II. Рассмотрим в этом пункте задачу Коши
,
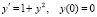решением которой является тригонометрическая функция y = tgx [4]. Для нахождения значений тригонометрической функции y = tgx воспользуемся разложением функции в цепную дробь
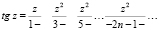
для комплексных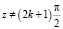 
, k – целое [5].
Ниже приводится код программы в среде Delphi для нахождения значений тригонометрической функции tgx и, приведены значения данной функции с точностью до 15-го знака по указанной формуле при помощи подходящих дробей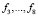 
для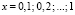 
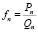, с использованием FR-алгоритма (прямого рекуррентного алгоритма). Этот алгоритм заключается в применении рекуррентных формул 
, 
, 
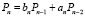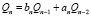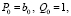
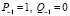. При этом мы получаем значения 
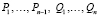и, совершив еще n – 1 делений, мы получаем значения 
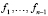. Общее число арифметических операций для нахождения 
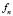– 4n умножений, n сложений и одно деление.
При использовании FR-алгоритма трудность состоит в том, что даже если последовательность {fn} будет сходиться к конечному пределу, последовательности числителей {Pn} и знаменателей {Qn} подходящих дробей могут одновременно стремиться к 0 или к ∞, что требует время от времени выполнять перемасштабирование, чтобы не было машинного переполнения или исчезновения порядка [1].
,
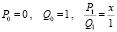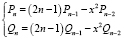при n ≥ 2,
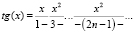
III. Создание программы в среде Delphi.
Процесс конструирования формы:
– для Form1 меняем значение в свойстве Caption на tg x;
– устанавливаем на форму компонент Panel1 со страницы Standard (удаляем значение в свойстве Caption для этого компонента, в свойстве Align выбираем значение alclient, меняем значение в свойстве Name для этого компонента на P1);
– устанавливаем на форму компоненты Label1 и Label2 со страницы Standard (меняем в свойстве Caption значение для этих компонент на Таблица результатов и Таблица погрешностей соответственно, в свойстве Font выбираем атрибуты шрифта: стиль – полужирный курсив, размер – 24, меняем значение в свойстве Name для этих компонент на L1 и L2 соответственно);
– устанавливаем на форму компоненты StringGrid1 и StringGrid2 со страницы Additional (меняем в свойствах ColCount и RowCount значения для этих компонент на 7 и 11 соответственно, меняем значение в свойстве Name для этих компонент на q1 и q2 соответственно);
– устанавливаем на форму компонент BitBtn1 со страницы Additional (меняем в свойстве Caption значение для этого компонента на Расчет, в свойстве Font выбираем атрибуты шрифта: стиль – полужирный курсив, размер – 24, меняем значение в свойстве Name для этого компонента на B1).
Код программы в среде Delphi имеет вид
unit fun;
{определяет внешнюю видимость этого модуля}
interface
{использование модулей}
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, Grids, StdCtrls, Buttons, ExtCtrls;
{объявление объектов}
type
TForm1 = class(TForm)
P1: TPanel;
q1: TStringGrid;
q2: TStringGrid;
B1: TBitBtn;
L1: TLabel;
L2: TLabel;
procedure P1Click(Sender: TObject);
procedure B1Click(Sender: TObject);
private
{ Private declarations }
{описанные в этой секции элементы недоступны извне (за пределами класса)}
public
{ Public declarations }
{описанные в этой секции элементы доступны всем}
end;
var
Form1: TForm1;
implementation {осуществляет интерфейс этого модуля}
{$R *.dfm} {включить определения формы}
{обработчик события onClick для компонента P1}
procedure TForm1.P1Click(Sender: TObject);
var h:integer;
x:real;
begin
{заполнение 1-го столбца таблицы результатов и таблицы погрешностей}
q1.Cells[0,0]:='N=';
q2.Cells[0,0]:='N=';
x:=0.1;
for h:=1 to 10 do
begin
q1.Cells[0,h]:='x='+floattostr(x);
q2.Cells[0,h]:='x='+floattostr(x);
x:=x+0.1;
end;
{заполнение 1-й строки таблицы результатов и таблицы погрешностей}
for h:=1 to 6 do
begin
q1.Cells[h,0]:=floattostr(h+2);
q2.Cells[h,0]:=floattostr(h+2);
end;
end;
{обработчик события onClick для компонента B1 (заполнение таблицы результатов и таблицы погрешностей)}
procedure TForm1.B1Click(Sender: TObject);
Var z:array[1..10,1..10] of real;
y,b,r:real;
m,h,l,t:integer;
Begin
for t:=1 to 6 do
begin
for l:=1 to 10 do
begin
y:=l*0.1;
for m:=3 to 8 do
begin
h:=m;
r:=0;
b:=y*y/(2*m-1);
h:=h-1;
while h>0 do
begin
r:=y*y/(2*h-1-b);
b:=r;
h:=h-1;
end;
r:=r/y;
z[l,n]:=abs(r-sin(y)/cos(y));
q1.Cells[t,l]:=Format (‘ %e’, [r]);
end;
end;
for l:=1 to 10 do
begin
for m:=3 to 8 do
q2.Cells[t,l]:=Format ('%e', [z[l,m]]);
end;
end;
end;
end. [6]
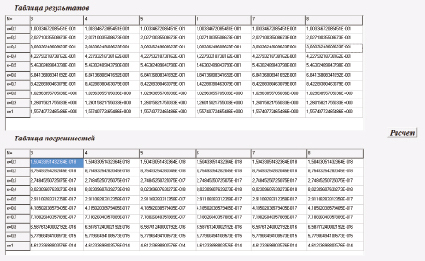
Скриншот окна формы в среде Delphi
Заключение
Исходя из полученных выше результатов видно, что цепные дроби являются наилучшим аппаратом приближения. Таким образом, приближение подходящими дробями дает большую точность.
Библиографическая ссылка
Рагимханова Г.С., Кулиева Д.Р., Рагимханова А.Р., Гаджиева З.Д. СВЯЗЬ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ РАЗЛИЧНЫХ ВИДОВ И ПРИБЛИЖЕНИЕ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ЦЕПНЫМИ ДРОБЯМИ С ИСПОЛЬЗОВАНИЕМ СРЕДЫ ПРОГРАММИРОВАНИЯ // Фундаментальные исследования. – 2017. – № 12-1. – С. 110-114;URL: https://fundamental-research.ru/ru/article/view?id=41988 (дата обращения: 18.04.2024).