Высокая мобильность населения в крупных городах, большое количество автовладельцев привели к критическому состоянию загруженности улично-дорожных сетей. Расширение транспортной сети часто невозможно как в силу градостроительных особенностей, так и по причине недостатка материальных ресурсов. Поэтому актуальная задача – оптимальное распределение транспортных потоков по уже существующей транспортной сети.
Изучением этого вопроса занимаются как зарубежные, так и отечественные ученые с середины прошлого столетия. Разработаны различные математические модели и программные продукты, позволяющие решать отдельные транспортные задачи как локального, так и глобального характера. Развитие информационных технологий позволило значительно сократить время, необходимое для получения итогового результата. Однако развитие транспортной инфраструктуры ставит все новые задачи, а достижения в IT-технологиях предоставляют все новые возможности. В последнее время к решению задач в данной области привлекаются Интеллектуальные транспортные системы (ИТС). Развитие и внедрение ИТС позволяет получать данные о текущих транспортных условиях. Поэтому разработка математических моделей и соответствующих программ, которые бы строили стратегию управления не по заранее рассчитанным планам, а моделировали ситуацию по реальным условиям с краткосрочной задержкой, весьма актуальна.
Цель исследования: управление транспортными потоками в режиме реального времени с целью оптимизации транспортных задержек.
В силу того, что транспортный поток является стохастическим, а дорожные условия могут очень быстро меняться, проблема выбора оптимальной стратегии управления дорожным движением в реальном времени является очень сложной. Причиной транспортных заторов зачастую является неэффективная организация движения на перекрестках, в частности на перекрестках со светофорным регулированием. Поэтому моделированию движения на регулируемых перекрестках и определению оптимальных параметров светофорного регулирования посвящено множество исследований [1–3]. Цель исследования определяет выбор метода моделирования. Микроскопические модели позволяют учитывать большое количество факторов, влияющих на итоговый результат, но не применимы в режиме онлайн. С помощью макроскопических моделей результат может быть получен быстро, но с недостаточной точностью.
Существуют различные программы, моделирующие движение транспортных средств как на отдельных локальных участках, так и на всей дорожной сети в целом. Например, TRANSYT, SCOOT [4] и SCATS [5] позволяют разрабатывать стратегии управления в режиме онлайн, однако по заранее вычисленным планам. В более поздних исследованиях для моделирования транспортной ситуации было предложено использовать метод нейронных сетей. Однако калибровка таких моделей может занимать много времени и задействует большой объем данных.
ACO (Ant Colony) – алгоритм, применяемый в последнее время к решению оптимизационных задач в области транспортных потоков, по мнению исследователей [6], достаточно быстрый и эффективный и может пррименяться для решения задач управления потоками в режиме реального времени. Данный алгоритм реализован, например, в программе ACOTRANS для решения проблемы координации светофорной сигнализации.
Для координации светофорной сигнализации с целью снижения вероятности блокировки отдельных перекрестков также существуют различные программы: Synchro, PASSER, aaSIDRA, SCOOT, SCATS, TRANSYT. Однако вопрос об одновременном выполнении сразу двух условий – точность и скорость в расчетах – по прежнему остается открытым.
Мезоскопическая модель TIMeR_Mod, разработанная авторами, рассматривает в деталях каждый узел транспортной сети. В данной модели они классифицируются на узлы со светофорным регулированием, без светофорного регулирования, кольцевые пересечения. Для расчетов показателей эффективности в узловых точках требуется информация обо всех входящих конфликтующих потоках. Но объем такой информации сведен к минимуму. Авторами ранее доказано, что интервалы по времени между автомобилями в потоке распределены по обобщенному закону Эрланга, определены методы мониторинга и обработки такой информации. Дальнейшие расчеты ведутся аналитическими методами, что позволяет мгновенно выдавать результат. Поэтому авторская модель TIMeR_Mod [7] применима для определения параметров эффективности организации движения в динамическом режиме.
В модели TIMeR_Mod улично-дорожная сеть (УДС) представлена связанными матрицами ASTREETS и BINTERSECTION. Строка матрицы ASTREETS содержит информацию об узловой точке, образованной пересечениями улиц S1 и S2 , и о перегоне между узловыми точками 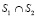 и
и 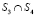 . Строка матрицы BINTERSECTION содержит информацию о входящих и исходящих транспортных потоках для точки
. Строка матрицы BINTERSECTION содержит информацию о входящих и исходящих транспортных потоках для точки 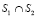 . Методы обновления информации в вышеуказанных матрицах по данным мониторинга улично-дорожной сети приведены в работе [8].
. Методы обновления информации в вышеуказанных матрицах по данным мониторинга улично-дорожной сети приведены в работе [8].
Определение оптимальной длительности цикла и фаз регулирования в динамическом режиме
По исходным данным, содержащимся в матрицах ASTREETS и BINTERSECTION модели TIMeR_Mod возможно в режиме реального времени с краткосрочной задержкой реагирования определять оптимальные параметры светофорного регулирования на пересечении многополосных дорог. Ниже приведем метод, разработанный авторами статьи, и его обоснование.
Введены следующие обозначения:
TgI – время, в течение которого разрешено движение на дороге I;
TgII – время, в течение которого разрешено движение на дороге II;
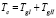 – длина цикла регулирования;
– длина цикла регулирования;
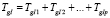 ,
,
где TgIi – разрешено движение на дороге I в i-ом направлении (тогда в течение времени T – TgIi движение на дороге I в i-ом направлении запрещено);
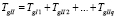 ,
,
где TgIi – разрешено движение на дороге II в j-м направлении (тогда в течение времени T – TgIIj движение на дороге I в j-м направлении запрещено)
Существуют различные определения задержки у перекрестка. Под задержкой на регулируемом перекрестке в авторской модели понимается время простоя в случае, если движение в данном направлении запрещено.
Средняя часовая задержка за один цикл регулирования на регулируемом перекрестке (при условии, что очередь не накапливается):
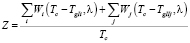 .
.
В работе [7] определен вид функции W(Ti, λ) при различных значениях параметра λ:
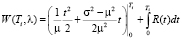 .
.
Поставим задачу минимизации средней часовой задержки транспортных средств:
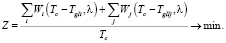 (1.1)
(1.1)
Условие ликвидации очереди за цикл регулирования по всем направлениям:
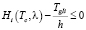 ,
, 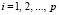 ; (1.2)
; (1.2)
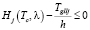 ,
, 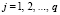 .
.
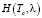 – функция восстановления, выражает количество автомобилей, прибывающих к перекрестку за время Tc.
– функция восстановления, выражает количество автомобилей, прибывающих к перекрестку за время Tc.
Пусть NI – интенсивность потока в направлении I. Ее можно представить в виде суммы интенсивностей по всем направлениям дороги I:
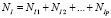 .
.
Аналогично для дороги II:
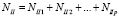 .
.
Замечание: если в течение времени TgIi (или TgIIi) движение разрешено на нескольких полосах для движения ТС, то интенсивность на этих полосах суммируется и обозначается как NgIi (или NgIIi).
Примем,что распределение фаз регулирования пропорционально интенсивности движения:
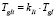 , (1.3)
, (1.3)
где 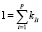 ,
, 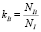 – для дороги I.
– для дороги I.
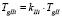 , (1.4)
, (1.4)
где 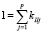 ,
, 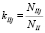 – для дороги II.
– для дороги II.
При этом
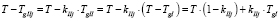 . (1.5)
. (1.5)
Рассмотрим задачу математического программирования (1.1–1.2). Функция (1.1) является функций двух независимых переменных T = Tc и TgI. Найдем частные производные целевой функции по этим переменным, учитывая равенства (1.3–1.5):
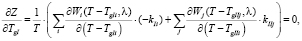 (1.6)
(1.6)
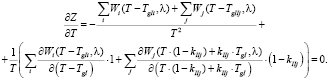 (1.7)
(1.7)
Заметим, что 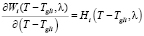 и
и 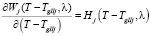 – возрастающие функции первого аргумента.
– возрастающие функции первого аргумента.
Оценим (1.7):
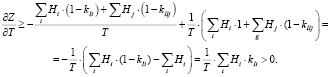
Следовательно уравнение (1.7) не имеет решений, тогда функция (1.1) не имеет критических точек внутри области определения. Поэтому задача математического программирования (1.1–1.2) может иметь решения только на границе области определения.
Для решения задачи (1.1–1.2) будем составлять фунцию Лангранжа, поочередно представляя одно из условий (1.2) в виде равенства
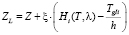 . (1.8)
. (1.8)
Переменные задачи: T, TgI, ξ. Здесь ξ – множитель Лагранжа.
(1.9)
(1.10)
(1.11)
При составлении системы использовали тот факт, что
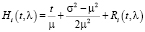 .
.
Математическое ожидание M(T) и дисперсия D(T) для обобщенного закона Эрланга следующие:
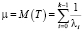 ;
; 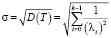 .
.
Ранее авторами доказано, что функция R(t) может состоять только из следующих слагаемых:
1) 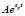 ;
;
2) 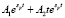 ;
;
3) 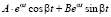 .
.
Тогда производная по переменной t в каждом из этих случаев соответственно следующая:
1) 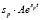 ;
;
2) 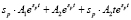 ;
;
3) 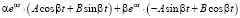 .
.
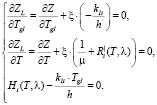

Последовательность регулируемых перекрестков
Система (1.9–1.11) решается численно, например, с помощью систем Maple или MatLab. После решения полученной системы проверяем выполнение всех условий (1.2).
Среди всех найденных точек выбираем ту, для которой целевая функция принимает минимальное значение.
Ранее [9] авторами была решена аналогичная задача для случая пересечения двухполосных дорог.
Метод управления движением во время заторов
Рассмотрим серию перекрестков  (рисунок). И пусть Int1 – единственный из них, у которого интенсивность превышает пропускную способность по указанному направлению («узкое место»). В этом случае очередь у перекрестка будет накапливаться при любом режиме регулирования, так как условие (1.2) хотя бы для одного из направлений не выполняется. Задачей управления в этом случае является не допустить блокировку соседнего перекрестка Int2.
(рисунок). И пусть Int1 – единственный из них, у которого интенсивность превышает пропускную способность по указанному направлению («узкое место»). В этом случае очередь у перекрестка будет накапливаться при любом режиме регулирования, так как условие (1.2) хотя бы для одного из направлений не выполняется. Задачей управления в этом случае является не допустить блокировку соседнего перекрестка Int2.
В работе [8] авторами описан метод обновления исходных данных для модели TIMeR_Mod. Это позволяет отследить и предсказать возможность появления «затора» у перекрестка.
Избыток автомобилей за один цикл в выбранном направлении (накопившаяся за один цикл очередь):
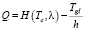 ,
,
где Tc – длина цикла регулирования, TgI – разрешено движение на дороге I в выбранном направлении, h – интервал между отбывающими с перекрестка автомобилями, 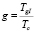 – относительная фаза зеленого сигнала.
– относительная фаза зеленого сигнала.
Очередь начинает накапливаться у конкретного регулируемого перекрестка при выполнении условия
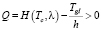 .
.
Ниже используются следующие обозначения:
ci, 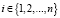 – относительная пропускная способность перекрестка Inti;
– относительная пропускная способность перекрестка Inti;
gi, 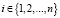 – относительная фаза зеленого сигнала на Inti;
– относительная фаза зеленого сигнала на Inti;
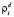 ,
, 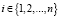 – относительная интенсивность потока, убывающего с перекрестка Inti (в данном направлении);
– относительная интенсивность потока, убывающего с перекрестка Inti (в данном направлении);
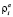 ,
, 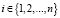 – относительная интенсивность потока, прибывающего на Inti (в данном направлении).
– относительная интенсивность потока, прибывающего на Inti (в данном направлении).
Причем 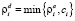 .
.
Так как по условию Int1 – «узкое место», то выполняется неравенство: 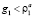 . Относительная интенсивность прибытий в выбранном направлении перед перекрестком Int1 складывается из ρstr (автомобили, совершавшие движение в направлении Int3 → Int2 → Int1) и ρad2 (автомобили, примкнувшие к этому направлению на перекрестке Int2):
. Относительная интенсивность прибытий в выбранном направлении перед перекрестком Int1 складывается из ρstr (автомобили, совершавшие движение в направлении Int3 → Int2 → Int1) и ρad2 (автомобили, примкнувшие к этому направлению на перекрестке Int2): 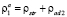 .
.
1 случай. Для всех остальных перекрестков 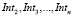 выполняется неравенство:
выполняется неравенство: 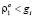 ,
, 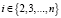 .
.
Тогда для сдерживания распространения очереди изменим фазы регулирования на Int2: 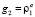 . То есть фазе зеленого сигнала на Int2 дадим значение относительной интенсивности прибытий к Int1.
. То есть фазе зеленого сигнала на Int2 дадим значение относительной интенсивности прибытий к Int1.
Если при этом очередь у Int2 начнет блокировать Int3, примем 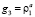 . И так далее.
. И так далее.
Регулируя таким образом в динамическом режиме светофорную сигнализацию, можно перераспределить очередь между перекрестками 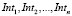 и избежать блокировки перекрестка Int2. Причем смену фаз необходимо провести менее, чем за время
и избежать блокировки перекрестка Int2. Причем смену фаз необходимо провести менее, чем за время 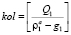 циклов.
циклов.
2 случай. Если 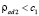 , а
, а 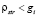 , то на перекрестке Int2 примем:
, то на перекрестке Int2 примем: 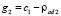 .
.
Если при этом очередь у Int2 начнет блокировать Int3, примем: 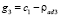 . И так далее.
. И так далее.
3 случай. Если 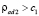 , то ликвидировать очередь у Int1 можно только за счет перераспределения транспортных потоков по сети. Модель TIMeR_Mod позволяет это сделать путем выбора маршрута с наименьшими транспортными затратами [Naumova, Danovich, 2014].
, то ликвидировать очередь у Int1 можно только за счет перераспределения транспортных потоков по сети. Модель TIMeR_Mod позволяет это сделать путем выбора маршрута с наименьшими транспортными затратами [Naumova, Danovich, 2014].
Заключение
Скопление транспортных средств в узловых точках улично-дорожной сети – одна из основных причин транспортных заторов. Исследования авторов статьи направлены на решение данной проблемы. Методы решения базируются на собственной модели распределения транспортных потоков, которая выгодно отличается от уже существующих адекватным сочетанием точности расчетов и скорости вычислений. Задачи по управлению движением автотранспортных средств в модели TIMeR_Mod решаются без привлечения имитационного моделирования, что позволяет оперативно получать результат в динамическом режиме.
Работа выполнена при поддержке РФФИ и администрации Краснодарского края, проект № 16-48-230720 р_а.
Библиографическая ссылка
Наумова Н.А., Карачанская Т.А., Хачатурян М.К. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ТРАНСПОРТНЫХ ПОТОКОВ В ДИНАМИЧЕСКОМ РЕЖИМЕ // Фундаментальные исследования. – 2017. – № 12-2. – С. 312-317;URL: https://fundamental-research.ru/ru/article/view?id=42021 (дата обращения: 20.04.2024).



