Расчет основных параметров гидротранспортирования монодисперсных смесей твердых материалов в вертикальных трубах в рамках общей физико-математической модели процесса их движения в вертикальном трубопроводе рассматривался в работе [1]. Метод расчета строился на основе лагранжевого похода при моделировании движения двухфазных сред [2–4]. Ранее было показано, что расчеты по предложенному методу удовлетворительно согласуются с опубликованными экспериментальными данными для крупных частиц диаметром до d = 1,7 мм, для которых выполняется условие, что d > 0,015 D (D – внутренний диаметр трубы) [5]. В настоящей работе эта работа продолжена применительно к частицам меньшей дисперсности.
Цель работы
Целью настоящей работы является определение области применимости разрабатываемой физико-математической модели двухфазных потоков на основе сравнения собственных расчетных зависимостей с экспериментальными данными и результатами расчетов с использованием альтернативных подходов, опубликованными в научно-технической литературе.
Основные положения физико-математической модели
Используемая физико-математическая модель процесса движения двухфазной смеси основывается на следующих положениях.
1. Рассматривается стационарное (установившееся) движение двухфазной смеси.
2. Поскольку течение обладает осевой симметрией, течение в круглой вертикальной трубе представляется в виде суперпозиции плоских горизонтальных кольцевых слоев.
3. В кольцевом слое концентрация частиц твердой фазы постоянна.
4. Движение частиц в потоке жидкости представлено в виде суперпозиции движения в вертикальном направлении, параллельном оси трубы, и движения в горизонтальном направлении, перпендикулярном к ней.
5. Угловая скорость вращения частицы равна локальному градиенту скорости движения жидкости в продольном направлении.
6. Перемещение твердых частиц из области высокой концентрации в область низкой концентрации определяется процессом турбулентной диффузии частиц и действием сил Магнуса, Саффмана и турбофореза.
7. Взаимодействие частиц между собой ударное упругое.
8. Дробления или слипания частиц не происходит.
9. Диаметр трубопровода много больше диаметра частиц.
Физико-математическая модель движения мелких монодисперсных твердых частиц в потоке ньютоновской жидкости в вертикальных трубах, построенная в работе [1], основана на представлении, что твердые частицы следуют за мелкими турбулентными молями жидкости, а различия в их поведении можно учесть поправочными коэффициентами, определенными независимым расчетным путем. В этом случае, предполагается, что при движении гидросмеси вверх на частицы действует сила, создаваемая градиентом давления в жидкой среде Fp и сила Архимеда FA, направленные вверх, и силы тяжести Fg и сила гидродинамического сопротивления Fr направленные вниз. При движении гидросмеси вниз направление сил Fp и Fr изменяется на противоположное. В поперечном горизонтальном направлении на частицы действуют силы Магнуса FM, Саффмана FS и турбофореза Ftf. В поперечном направлении твердые частицы перемещаются за счет действия этих сил и процесса турбулентной диффузии, переносящей твердые частицы из области их большей объемной концентрации в область меньшей объемной концентрации. Поскольку частицы монодисперсны, предполагается, что столкновения между частицами не происходит, поскольку при лобовом упругом соударении частиц равной массы, скорости частиц после соударения не изменяются, а изменяется только направление движения на противоположное. Так как частицы тождественны, то после упругого соударения отраженная частица как бы продолжает движение частицы движущейся слева направо, а частица, перемещающаяся в противоположном направлении, как бы продолжает движение частицы, которая до удара перемещалась справа налево. В установившемся состоянии потоки перемещающихся частиц слева направо и, в противоположном направлении, справа налево, равны. Поскольку, как правило, сведений о гранулометрическом составе твердой фазы не приводится, примем, что частицы монодисперсны и сферичны.
Для определенности вначале рассмотрим направленное вверх, движение двухфазного потока монодисперсных твердых частиц в вертикальной трубе. Положим, что частицы имеют сферическую форму, имея в виду, что частицы несферической формы в гидродинамическом плане могут быть приведены к эквивалентной сферической частице, а поскольку частицы монодисперсны и скорости частиц в данной точке стационарны, полагаем также, что они контактно не взаимодействуют друг с другом. В вертикальном направлении на твердые частицы действуют силы давления Fp и сила FA, направленные вверх, и сила веса Fg и сила гидравлического сопротивления Fr, направленные вниз. Эти силы определяются следующими выражениями:
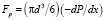 ,
,
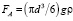 ,
,
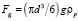 ,
,
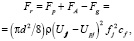 (1)
(1)
где (–dp/dx) – градиент давления в направлении движения, в рассматриваемом случае вверх; r – плотность жидкости; rp – плотность твердых частиц; g – гравитационное ускорение; Ufj и Upj – скорости движения жидкости и частиц в направлении движения потока вверх; fj – коэффициент стесненности, учитывающий стесненное движение жидкости в межчастичном пространстве; cf – коэффициент гидравлического сопротивления сферической частицы; j – номер кольцевого слоя.
Скорость частицы по отношению к жидкости определяется уравнением
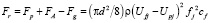 , (2)
, (2)
где
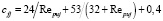 – коэффициент гидравлического сопротивления (3)
– коэффициент гидравлического сопротивления (3)
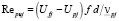 – число Рейнольдса, определенное по фактической скорости стесненного движения жидкости в межчастичном пространстве (Ufj – Upj)fj, диаметру частицы d,
– число Рейнольдса, определенное по фактической скорости стесненного движения жидкости в межчастичном пространстве (Ufj – Upj)fj, диаметру частицы d,
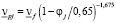 , кинематической вязкости смеси [6],
, кинематической вязкости смеси [6],
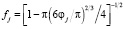 , – коэффициента стесненности жидкости [7],
, – коэффициента стесненности жидкости [7],
φj – объемная доля твердой фазы в j-м кольцевом слое; 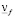 – кинематическая вязкость несущей жидкости.
– кинематическая вязкость несущей жидкости.
Подставляя выражения (1) и (3) в (2), получим кубическое уравнение относительно числа Рейнольдса 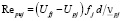 ,
,
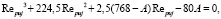 (4)
(4)
где 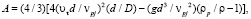 а
а 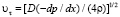 – динамическая скорость; D – внутренний диаметр трубы.
– динамическая скорость; D – внутренний диаметр трубы.
Уравнение (4) решается методом последовательных приближений. По найденному значению числа Рейнольдса 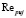 определяется величина разности скоростей жидкости и частицы
определяется величина разности скоростей жидкости и частицы
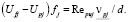
На основе модели Прандтля выражение для касательного трения в двухфазном потоке представляется в виде суммы сил трения, возникающих в жидкости при её движении, и сил трения, возникающих в жидкости при перемещении в ней твердых частиц [1]. При этом полагается, что пульсации скорости частиц определяются наличием пульсаций жидкости.
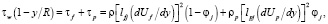 (5)
(5)
где lfj и lpj – длины пути смешения жидкой и твердой фазы двухфазного потока соответственно. В дальнейшем полагается, что длины путей смешения равны lf и lp, а величина lf, определяется интерполяционной зависимостью 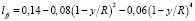 .
.
Из (6) получим общее выражение для расчета профиля скорости двухфазного потока, которое в случае монодисперсных частиц принимает вид
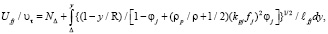 (6)
(6)
где 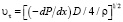 – динамическая скорость, определенная по величине диаметра трубы D; NΔ – относительная скорость двухфазной среды на расстоянии приповерхностной зоны течения [5]; Δ – толщина приповерхностной зоны течения [5]; kpj – коэффициент, определяемый отношением усредненного квадрата пульсационной скорости частицы к усредненному квадрату пульсационной скорости жидкости [1] при частоте ω, определяемой из решения задачи об осаждения частиц под действием силы тяжести [3]. Проведенные расчеты показали, что для частиц с плотностью большей плотности несущей жидкости значения kpj < 1, что согласуется с ожидаемым значением этой величины в двухфазном потоке, то есть амплитуда пульсаций скорости движения частиц меньше амплитуды пульсаций жидкости. Аналогичное положение имеет место и для поперечной составляющей пульсационной скорости твердых частиц и жидкости.
– динамическая скорость, определенная по величине диаметра трубы D; NΔ – относительная скорость двухфазной среды на расстоянии приповерхностной зоны течения [5]; Δ – толщина приповерхностной зоны течения [5]; kpj – коэффициент, определяемый отношением усредненного квадрата пульсационной скорости частицы к усредненному квадрату пульсационной скорости жидкости [1] при частоте ω, определяемой из решения задачи об осаждения частиц под действием силы тяжести [3]. Проведенные расчеты показали, что для частиц с плотностью большей плотности несущей жидкости значения kpj < 1, что согласуется с ожидаемым значением этой величины в двухфазном потоке, то есть амплитуда пульсаций скорости движения частиц меньше амплитуды пульсаций жидкости. Аналогичное положение имеет место и для поперечной составляющей пульсационной скорости твердых частиц и жидкости.
Величина NΔ определяется в виде зависимости
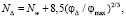 (7)
(7)
где Nw = 11,6 для гидравлически гладкой стенки трубы или 8,5 для предельно шероховатой поверхности трубы; φΔ – объемная доля частиц на расстоянии Δ от стенки трубы; φmax – максимальная объемная доля твердых частиц, соответствующая предельно шероховатой поверхности образованной осевшими частицами. Величина φmax зависит от формы частиц 0,524 (сферические частицы) ≤ φmax ≤ 1 (частицы в виде куба).
Второй член в правой части выражения (7) определяет проскальзывание (скачок скорости) на поверхности шероховатого квазитвердого тела, образованного двухфазным потоком вблизи поверхности трубы [5]. Величина Δ равна сумме толщин подслоев жидкости на гладкой или шероховатой поверхности стенки трубы δ и диаметра частиц d.
Разрешая выражение (6) относительно [ℓfj(dUf/dy)]2, запишем выражения сил Магнуса, Саффмана и турбофореза
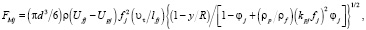 (8)
(8)
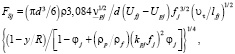 (9)
(9)
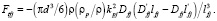 (10)
(10)
В последнем выражении штрих означает производную соответствующей функции по y. Коэффициент турбулентной диффузии двухфазного потока Dpj можно представить в виде зависимости
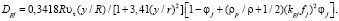 (11)
(11)
Скорость движения твердых частиц в поперечном направлении Vp определяется уравнением
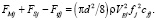 (12)
(12)
Из (12) получим
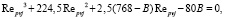 (13)
(13)
где 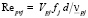 – число Рейнольдса, определенное по фактической скорости стесненного движения частицы относительно жидкости в межчастичном пространстве Vpj fj в поперечном направлении, диаметру частицы d и кинематической вязкости двухфазного потока
– число Рейнольдса, определенное по фактической скорости стесненного движения частицы относительно жидкости в межчастичном пространстве Vpj fj в поперечном направлении, диаметру частицы d и кинематической вязкости двухфазного потока 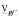
Величина B определяется выражением
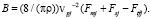 (14)
(14)
По известному значению числа Рейнольдса 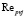 определяется скорость движения частицы относительно жидкости
определяется скорость движения частицы относительно жидкости
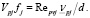
Распределение объемной доли твердой частиц, при установившемся осесимметричном движении двухфазного потока, в поперечном горизонтальном направлении описывается в виде
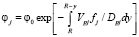 , (15)
, (15)
где φ0 – объемная доля твердой частиц на оси трубы.
Средняя объемной доли твердой частиц φm, объемный расход жидкой и твердой фаз и средняя скорость потока двухфазной среды Um определяется путем интегрирования соответствующих профилей по поперечному сечению трубы.
Полученные соотношения позволяют рассчитать все характеристики двухфазного потока монодисперсных твердых частиц. Задается произвольное значение объемной доли твердой частицы в центре потока φ0 и градиента давления (–dp/dx). Затем, на некотором выбранном малом расстоянии (шаге) dy, рассчитывается значение величины φ < φ0. После чего с помощью итераций определяются все характеристики потока с уточнением рассчитанного значения φ. Далее вычислительный процесс повторяется при новом шаге по dy. Параллельно аналогичный расчет выполняется и для распределения скорости. За счет варьирования величинами φ0 и градиента давления (–dp/dx) определяются значения, которые обеспечивают наилучшее соответствие с опытными данными по всей совокупности интегральных величин: градиенту давления, средней скорости и средней объемной доли твердой частиц.
В случае если движение двухфазного потока направлено вниз, то силы давления Fp и веса Fg направлены вниз, а сила Архимеда FA вверх, и в этом случае частицы движутся быстрее, чем жидкости, и приведенные расчетные соотношения модифицируются в соответствии с изменившимся направлениями действия сил. В этом случае в формуле (4) выражение для величины А принимает вид
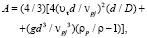
а в выражении (15) изменяется знак перед интегралом на противоположный.
Сравнение экспериментальных и расчетных данных
Изложенный выше метод расчета использовался для сравнения расчетных значений гидродинамических характеристик двухфазного потока с опытными данными, опубликованными в работе [8]. Отметим, что эти опытные данные до настоящего времени широко используются при сопоставлении опытных данных с разрабатываемыми методами расчета, см., например, [9]. В [8] приведены результаты гидравлических испытаний песка плотностью ρ = 2650 кг/м3 в виде трех фракций крупностью d = 175 мкм, d = 470 мкм и d = 780 мкм в трубопроводе диаметром D = 25,8 мм. Для всех трех песчаных смесей испытания проводились при трех значениях объемной доли твердой фазы φ = 0,1, φ = 0,3 и φ = 0,4. В проведенных опытах варьировалась величина градиента давления (–dp/dx) в диапазоне от 12 кПа/м до 31 кПа/м.
В опытах измерялось распределение объёмной доли твердой фазы φ и локальной скорости U в зависимости от безразмерной координаты y/R (y – расстояние от стенки трубы; R – радиус трубы) и средняя скорость Um, которые находились в диапазоне от 1,7 м/с до 6,9 м/с.
Сравнение опытных и расчетных интегральных значений гидродинамических характеристик двухфазного потока приведено в таблице.
На рис. 1, a, представлены экспериментальные и расчетные значения объемной доли твердой фазы, а на рис. 1, б–г, профиля скорости в вертикальном диаметральном сечении трубопровода при крупности песчаных частиц d = 175 мкм. В целом имеет место достаточно хорошее соответствие между опытными и расчетными величинами, как по величине φm, так и по профилю скорости U.
На рис. 2, а представлены экспериментальные и расчетные значения объемной доли твердой фазы, а на рис. 2, б–г, профиля скорости в вертикальном диаметральном сечении трубопровода при крупности песчаных частиц d = 470 мкм. В целом также имеет место достаточно хорошее соответствие между опытными и расчетными величинами, как по величине φm, так и по профилю скорости U.
На рис. 3, а, представлены экспериментальные и расчетные значения объемной доли твердой фазы, а на рис. 3, б–г, профиля скорости в вертикальном диаметральном сечении трубопровода при крупности песчаных частиц d = 780 мкм. В этом случае также имеет место достаточно хорошее соответствие между опытными и расчетными величинами, как по величине φ, так и по профилю скорости U.
В данном случае выполняется условие d > 0,015 D, в соответствии с которым расчет проводится по методике, изложенной в работе [5]. На рис. 4, а–г, представлены результаты сопоставления опытных и расчетных данных. В этом случае соответствие между опытными и расчетными величинами также достаточно удовлетворительное.
Из сравнения расчетных зависимостей, приведенных на рис. 3 и 4, с опытными данными, видно, что в последнем случае имеется лучшее согласие между опытными данными и расчетными зависимостями по распределению объемной доли твердой фазы и профиля скорости при φ = 0,1 и несколько худшее при φ = 0,3 и φ = 0,4. Следовательно. для крупных частиц (d > 0,015 D) предпочтительно использование метода расчета, изложенного в [5].
Сравнение опытных и расчетных значений интегральных величин: гидравлического уклона, средней скорости и средней объемной доли твердой фазы
|
d = 175mm |
d = 470mm |
d = 780mm |
|||||||||
|
Эксперимент |
Расчет |
Эксперимент |
Расчет |
Эксперимент |
Расчет |
||||||
|
i |
Um(м/с) |
i |
Um(м/с) |
i |
Um(м/с) |
i |
Um(м/с) |
i |
Um(м/с) |
i |
Um(м/с) |
|
φ = 0,1 |
|||||||||||
|
0,262 |
2,8 |
0,275 |
2,76 |
0,058 |
1,85 |
0,091 |
1,84 |
0,109 |
1,75 |
0,118 |
1,73 |
|
0,568 |
3,85 |
0,544 |
3,9 |
0,262 |
2,85 |
0,219 |
2,86 |
0,313 |
2,9 |
0,307 |
2,95 |
|
0,772 |
4,8 |
0,798 |
4,73 |
0,466 |
3,85 |
0,395 |
3,84 |
0,517 |
3,85 |
0,507 |
3,88 |
|
1,078 |
5,8 |
1,098 |
5,55 |
0,670 |
4,8 |
0,613 |
4,78 |
0,721 |
4,75 |
0,721 |
4,74 |
|
1,465 |
6,9 |
1,511 |
6,5 |
0,976 |
5,8 |
0,911 |
5,82 |
1,027 |
5,8 |
1,022 |
5,85 |
|
1,383 |
6,8 |
1,237 |
6,78 |
1,383 |
6,9 |
1,325 |
6,95 |
||||
|
φ = 0,3 |
|||||||||||
|
0,340 |
2,95 |
0,324 |
3,01 |
0,289 |
2,85 |
0,289 |
2,972 |
0,136 |
1,83 |
0,133 |
1,84 |
|
0,595 |
4,01 |
0,570 |
4,05 |
0,493 |
3,95 |
0,493 |
3,884 |
0,289 |
2,87 |
0,292 |
2,85 |
|
0,850 |
4,93 |
0,853 |
4,9 |
0,748 |
4,9 |
0,748 |
4,782 |
0,493 |
3,88 |
0,507 |
3,87 |
|
1,186 |
5,85 |
1,218 |
5,83 |
0,951 |
5,75 |
0,951 |
5,394 |
0,697 |
4,7 |
0,716 |
4,68 |
|
1,573 |
6,85 |
1,628 |
6,8 |
1,308 |
6,8 |
1,308 |
6,32 |
1,002 |
5,75 |
1,026 |
5,7 |
|
1,257 |
6,4 |
1,252 |
6,35 |
||||||||
|
φ = 0,4 |
|||||||||||
|
0,277 |
2,7 |
0,271 |
2,68 |
0,175 |
1,7 |
0,175 |
2,206 |
0,124 |
1,83 |
0,145 |
1,79 |
|
0,583 |
3,85 |
0,589 |
3,84 |
0,328 |
3 |
0,328 |
3,023 |
0,328 |
2,78 |
0,337 |
2,8 |
|
0,888 |
4,85 |
0,881 |
4,88 |
0,481 |
3,85 |
0,481 |
3,663 |
0,532 |
3,88 |
0,538 |
3,85 |
|
1,194 |
5,85 |
1,206 |
5,82 |
0,685 |
4,8 |
0,685 |
4,37 |
0,736 |
4,89 |
0,775 |
4,86 |
|
1,602 |
6,89 |
1,690 |
6,85 |
1,041 |
5,8 |
1,041 |
5,392 |
1,143 |
5,98 |
1,135 |
5,97 |
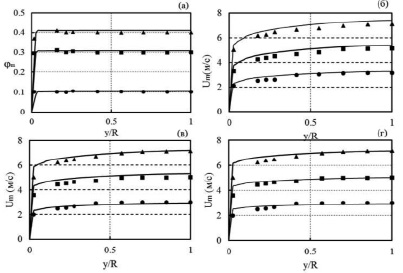
Рис. 1. Распределение объемной доли и скорости мелких частиц d = 175 мкм в вертикальной трубе с D = 25,8 мм: (а). φm = 0,1; φm = 0,3; φm = 0,4. (б). φm = 0,1; Um = 2,74 м/с; Um = 4,45 м/с; Um = 6,30 м/с. (в). φm = 0,3; Um = 2,64 м/с; Um = 4,58 м/с; Um = 6,4 м/с. (г). φm = 0,4; Um = 2,69 м/с; Um = 4,46 м/с; Um = 6,44м/с; •, ■, ▲ – опытные данные [8]; сплошные линии: расчет авторов
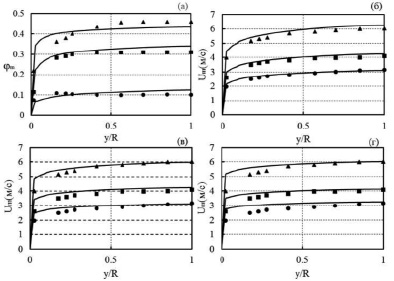
Рис. 2. Распределение объемной доли и скорости средних частиц d = 470 мкм в вертикальной трубе с D = 25,8 мм: (а). φm = 0,1; φm = 0,3; φm = 0,4. (б). φm = 0,1; Um = 2,63 м/с; Um = 3,58 м/с; Um = 5,29 м/с. (в). φm = 0,3; Um = 2,8 м/с; Um = 3,71 м/с; Um = 5,29 м/с. (г). φm = 0,4; Um = 2,80 м/с; Um = 3,66 м/с; Um = 5,33 м/с; ●, ■, ▲ – опытные данные [8]; сплошные линии: расчет авторов
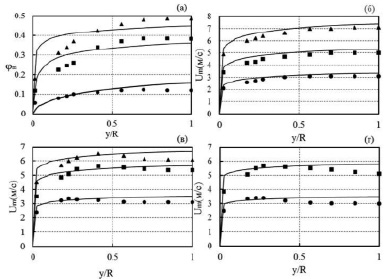
Рис. 3. Распределение объемной доли и скорости крупных частиц d = 780 μm в вертикальной трубе с D = 25,8 мм: (а). φm = 0,1; φm = 0,3; φm = 0,4. (б). φm = 0,1; Um = 2,78 м/с; Um = 4,43 м/с; Um = 6,24 м/с. (в). φm = 0,3; Um = 3,10 м/с; Um = 5,09 м/с; Um = 5,89 м/с. (г). φm = 0,4; Um = 3,14 м/с; Um = 5,25м/с; ●, ■, ▲ – опытные данные [8]; сплошные линии: расчет авторов
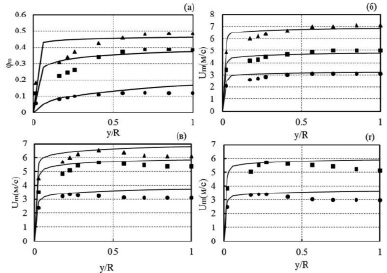
Рис. 4. Распределение объемной доли и скорости крупных частиц d = 780 мкм в вертикальной трубе с D = 25,8 мм: (а). φm = 0,1; φm = 0,3; φm = 0,4. (б). φm = 0,1; Um = 2,75 м/с; Um = 4,23 м/с; Um = 5.94 м/с. (в). φm = 0,3; Um = 3,11 м/с; Um = 4.95 м/с; Um = 5,89 м/с. (г). φm = 0,4; Um = 3,14 м/с; Um = 5,05м/с; ●, ■, ▲ – опытные данные [8]; сплошные линии: расчет авторов
Заключение
В работе показано, что сформулированный метод расчета движения двухфазных потоков в вертикальных трубах достаточно удовлетворительно согласуется с опытными данными, как по интегральным характеристикам двухфазного потока (средней скорости, гидравлического уклона, средней объемной доли твердой фазы), так и по локальному распределению скорости и объемной доли твердой фазы. Следует также отметить, что в разработанном методе расчета не используются какие-либо коррелирующие зависимости, полученные в результате сопоставления опытных и расчетных данных. Полученные результаты служат основанием для рекомендации изложенного метода расчета двухфазных потоков в вертикальных трубах для практических расчетов в инженерной практике.
Библиографическая ссылка
Кондратьев А.С., Ньа Т.Л. РАСЧЕТ ГИДРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ ПРИ ДВИЖЕНИИ ДВУХФАЗНОЙ СМЕСИ С МОНОДИСПЕРСНЫМИ ЧАСТИЦАМИ МЕЛКОЙ И СРЕДНЕЙ КРУПНОСТИ В ВЕРТИКАЛЬНЫХ ТРУБАХ // Фундаментальные исследования. – 2018. – № 4. – С. 13-20;URL: https://fundamental-research.ru/ru/article/view?id=42111 (дата обращения: 23.04.2024).



