Проблематика оценки и учета риска при выборе стратегии и тактики развития социально-экономических систем различного уровня – актуальная задача, рассмотрению которой посвящены работы цитируемых ниже Ф. Найта [1], Д. Власова [2], В. Гранатурова [3], И. Киселевой [4], А. Мищенко [5], В. Ступакова и Г. Токаренко [6], Н. Тихомирова [7], Л. Тэпмана [8], М. Халикова [9–11], А. Шеремета [12] и др. Актуальной является также проблематика классификации объектов социально-экономической природы по уровню риска с целью выбора приоритетных стратегий развития этих систем в условиях высокой неопределенности макросреды их функционирования. Например, в работе [9] рассматривалась проблема кластеризации российских регионов по уровню социально-экономической безопасности. Для упрощения численного алгоритма решения этой и аналогичных задач классификации объектов социально-экономической природы авторы использовали интегральный показатель экономической безопасности региона в форме индекса, представляющего собой взвешенную сумму частных показателей безопасности жизненно важных сфер экономики и социальной сферы региона. Та же идея, но в приложении к крупным интегрированным структурам и, в частности, к вертикально-интегрированным холдингам использована и в работе М.А. Халикова [13]. В более поздней работе этого автора и его учеников [10] обобщены результаты кластеризации предприятий крупных промышленных компаний и вертикально-интегрированных холдингов по выбранному показателю риска.
Отметим, что такой подход является серьезным упрощением реальной картины, так как не раскрывает всей природы риска [7, 8] и концентрирует риск либо в одной сфере деятельности компании, либо заменяет этот риск каким-либо внешним или внутренним (например, рыночным) [4, 14].
Более корректным является подход, основанный на классификации объектов социально-экономической природы по однородным группам с использованием векторного критерия, компонентами которого являются показатели риска в отдельных сферах, по которым осуществляется оценка финансово-экономических результатов деятельности элементов социально-экономической системы. Цель исследования состоит в том, чтобы предложить подход к решению задачи кластеризации объектов социально-экономической природы, что позволит оценить различия между объектами.
Материалы и методы исследования
Рассмотрим эту задачу более подробно. Ниже представлена методология решения этой проблемы, включающая концепцию и численный алгоритм кластеризации сложной, многоуровневой социально-экономической системы по векторному критерию.
Для классификации элементов сложной социально-экономической системы по группам риска необходимо решить следующие задачи:
– выбрать и обосновать состав показателей риска;
– проверить возможность оценки выбранных показателей, а также возможность актуализации результатов при получении новых данных (например, на последующих временных интервалах);
– выбрать соответствующую типу исходных данных метрику признакового пространства;
– определить и обосновать количество групп риска;
– предложить метод кластеризации, основанный на инструментарии многомерного статистического анализа и позволяющий построить устойчивую кластеризацию. Устойчивость кластеризации необходима для обеспечения необходимого уровня качества модели.
Приведем возможный вариант и математическую модель решения поставленной проблемы. Введем следующие обозначения:
n – число объектов;
m – число критериев (признаков);
i – номер объекта, 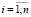 ;
;
j – номер признака (показателя риска) 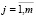 ;
;
xij – значение j-го признака для i-го объекта;
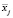 – среднее арифметическое j-го признака для всей совокупности объектов;
– среднее арифметическое j-го признака для всей совокупности объектов;
σj – среднеквадратическое отклонение для j-го признака;
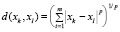 – расстояние между k-м и l-м объектами в общем виде рассчитываемое по формуле, приведенной в работе Н. Тихомирова, Т. Тихомировой и О. Ушмаева [15]. Параметр p устанавливается в зависимости от выбранной метрики.
– расстояние между k-м и l-м объектами в общем виде рассчитываемое по формуле, приведенной в работе Н. Тихомирова, Т. Тихомировой и О. Ушмаева [15]. Параметр p устанавливается в зависимости от выбранной метрики.
u – число кластеров;
Xr, Xq – r-й и q-й кластеры;
μr – центр r-го кластера.
Имея данные по показателям риска для каждого объекта необходимо провести стандартизацию данных с целью устранить негативный эффект влияния от масштаба. Стандартизация проводится по формуле [15–17]:
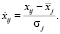 (1)
(1)
В результате стандартизации получим пригодные для исследования данные, по которым можно построить качественную модель кластеризации, независимую от разницы масштабов единиц измерения выбранных показателей риска.
Далее в зависимости от типа данных необходимо выбрать метрику признакового пространства. Метрика должна соответствовать типу данных для обеспечения точности модели кластеризации. Различают следующие виды расстояний [18]:
– евклидово расстояние – подходит для анализа количественных данных:
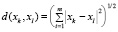 ; (2)
; (2)
– квадрат евклидова расстояния – также для оценки количественных данных, но эта метрика позволяет усилить различимость объектов в пространстве:
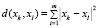 ; (3)
; (3)
– расстояние сити-блок – для анализа номинальных данных:
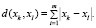 (4)
(4)
На следующем этапе на основе визуального анализа проводится исключение «нетипичных» объектов с целью получения устойчивой кластеризации. К «нетипичным» относятся объекты, значения показателей риска которых значительно отличаются от основной группы объектов. Внесение данных объектов в модель кластеризации приводит к некорректной классификации.
Далее определяется число классификационных групп по уровню риска. Для этого следует применить такой метод кластерного иерархического анализа, как метод дальнего соседа [19]. Согласно этому методу расстояние между кластерами рассчитывается на основе двух наиболее удаленных друг от друга объектов из разных кластеров по формуле
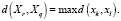 (5)
(5)
На следующем этапе проводится предварительная группировка предприятий одним из наиболее эффективных методов кластерного анализа – методом k-средних [15]. Суть метода состоит в расчете центров тяжести для каждого из кластеров. Далее измеряются расстояния от объектов до центров тяжести, на основе информации по которым объекты причисляются к ближайшему кластеру. Процедура повторяется до получения устойчивой кластеризации. При реализации этого метода минимизируется суммарное квадратичное отклонение точек кластеров от их центров:
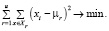 (6)
(6)
Результаты расчетов по методу k-средних позволяют получить устойчивую кластеризацию усеченного набора объектов исследуемой системы.
На завершающем этапе проводится попытка включения нетипичных объектов в модель кластеризации с использованием двойной проверки качества модели методами дискриминантного анализа и путем проверки гипотезы многомерного критерия Хотеллинга [18]. Благодаря дискриминантному анализу становится возможной расклассификация нетипичных объектов системы по кластерам. Построение дискриминантных функций по предварительно полученному разбиению позволяет также оценить вероятности отнесения объектов к тому или иному кластеру. Формула для расчета дискриминантных функций представлена ниже:
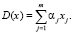 (7)
(7)
Дискриминантный анализ позволяет выявить ошибки в обучающей выборке.
Окончательная проверка качества полученной группировки реализуется с помощью критерия Хотеллинга – многомерного критерия, позволяющего проверить нулевую гипотезу о равенстве двух векторов математических ожиданий (центров групп). Формула для расчета статистики Хотеллинга выглядит следующим образом [15]:
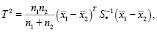 (8)
(8)
где 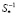 – матрица, обратная к матрице, составленной из центрированных значений i-й выборки.
– матрица, обратная к матрице, составленной из центрированных значений i-й выборки.
Таким образом, в случае, если нулевая гипотеза принимается, т.е. расчётное значение статистики Хотеллинга оказывается меньше, чем табличное значение критерия 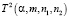 , то делается вывод о неразличимости двух центров групп, что в итоге позволяет объединить две группы в одну:
, то делается вывод о неразличимости двух центров групп, что в итоге позволяет объединить две группы в одну:
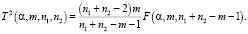 (9)
(9)
Также на основе расчётных значений статистики Хотеллинга:
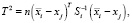 (10)
(10)
где Si – выборочная ковариационная матрица i-го кластера, 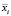 – вектор матожидания i-й группы, xj – вектор показателей j-го элемента выборки, осуществляется проверка гипотез о равенстве векторов, характеризующих уровень рисков нетипичных объектов, математическим ожиданиям центров групп.
– вектор матожидания i-й группы, xj – вектор показателей j-го элемента выборки, осуществляется проверка гипотез о равенстве векторов, характеризующих уровень рисков нетипичных объектов, математическим ожиданиям центров групп.
Нулевая гипотеза принимается, если расчётное значение статистики Хотеллинга оказывается меньше, чем табличное значение критерия. На основе 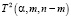 подтверждается или отклоняется гипотеза о равенстве вектора j-го объекта вектору матожидания i-го кластера, что ведет к отнесению этого объекта к i-й группе:
подтверждается или отклоняется гипотеза о равенстве вектора j-го объекта вектору матожидания i-го кластера, что ведет к отнесению этого объекта к i-й группе:
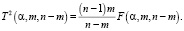 (11)
(11)
В противном случае подтверждается специфичность этих объектов, что приводит к невозможности их отнесения к той или иной группе и необходимости исследовать их обособленно от полученных кластеров.
По завершении приведенного алгоритма получаем качественную классификацию элементов социально-экономической системы по уровню риска.
Результаты исследования и их обсуждение
По предложенному алгоритму авторами были проведены расчеты на примере предприятий вертикально-интегрированного горно-металлургического холдинга АО «УГМК» (двадцать четыре предприятия) [20, 21].
Данные по уровням рисков рыночной деятельности, включаемым в векторный критерий кластеризации, рассчитаны по методу, приведенному в работе [11], и приведены в табл. 1. В цитируемой работе в качестве показателей риска рассматриваются: коэффициент расширенной автономии (Ка), коэффициент эффективности операционной сферы (ROA) и показатель эффективности инвестиционной сферы (ROAAM).
Была проведена стандартизация данных. Полученные значения показателей находятся в пределах от –2,9 до 3,5. Так как данные являются количественными и значения показателей лежат в достаточно узком интервале, было принято решение использовать метрику квадрата евклидова расстояния. В этом случае будет получена достаточная различимость объектов в признаковом пространстве.
На следующем этапе после очищения выборки от «нетипичных» предприятий – структурных бизнес-единиц (СБЕ) холдинга было установлено, что метод дальнего соседа подтверждает предположение о необходимости разбиения выборки на пять групп по уровню риска (рис. 1).
Таблица 1
Показатели риска предприятий холдинга АО «УГМК»
|
№ п/п |
Предприятие |
Коэффициенты |
||
|
Расширенной автономии |
Эффективности операционной сферы |
Эффективности инвестиционной сферы |
||
|
1 |
ООО «БАШМЕДЬ» |
0,241 |
0,085 |
0,195 |
|
2 |
АО «БУРИБАЕВСКИЙ ГОК» |
0,786 |
0,122 |
0,145 |
|
3 |
ПАО «ГАЙСКИЙ ГОК» |
0,558 |
0,066 |
0,083 |
|
4 |
ПАО «КЗОЦМ» |
0,525 |
0,062 |
0,110 |
|
5 |
ООО «ММСК» |
0,490 |
0,100 |
0,198 |
|
6 |
ПАО «РЗ ОЦМ» |
0,171 |
0,057 |
0,255 |
|
7 |
ПАО «РКЗ» |
0,689 |
0,073 |
0,079 |
|
8 |
АО «САФЬЯНОВСКАЯ МЕДЬ» |
0,705 |
0,242 |
0,375 |
|
9 |
АО «СВЕРДЛОВСКАВТОДОР» |
0,538 |
0,040 |
0,075 |
|
10 |
ПАО «СВЯТОГОР» |
0,663 |
0,083 |
0,117 |
|
11 |
АО «СИБИРЬ-ПОЛИМЕТАЛЛЫ» |
0,264 |
0,216 |
0,124 |
|
12 |
АО «СИБКАБЕЛЬ» |
0,665 |
0,087 |
0,117 |
|
13 |
ПАО «СУМЗ» |
0,125 |
0,146 |
0,291 |
|
14 |
АО «СУХОЛОЖСКОЕ ЛИТЬЕ» |
0,303 |
0,207 |
0,279 |
|
15 |
АО «УГМК – ВЦМ» |
0,126 |
0,027 |
0,219 |
|
16 |
АО «УК «КУЗБАССРАЗРЕЗУГОЛЬ» |
0,392 |
0,134 |
0,218 |
|
17 |
АО «УРАЛКАБЕЛЬ» |
0,493 |
0,089 |
0,181 |
|
18 |
АО «УРАЛЭЛЕКТРОМЕДЬ» |
0,738 |
0,153 |
0,182 |
|
19 |
АО «УРУПСКИЙ ГОК» |
0,859 |
0,183 |
0,207 |
|
20 |
АО «УЧАЛИНСКИЙ ГОК» |
0,793 |
0,086 |
0,101 |
|
21 |
ПАО «ЧЦЗ» |
0,816 |
0,156 |
0,194 |
|
22 |
АО «ШААЗ» |
0,596 |
0,084 |
0,134 |
|
23 |
АО «ЭКЗ» |
0,556 |
0,104 |
0,189 |
|
24 |
ПАО «ЭЛЕКТРОЦИНК» |
0,269 |
0,060 |
0,237 |
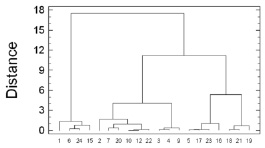
Рис. 1. Дендрограмма кластерного анализа предприятий холдинга АО «УГМК» методом «дальнего соседа»
Таблица 2
Распределение СБЕ АО «УГМК» по группам в соответствии с уровнем рисков рыночной деятельности методом k-средних
|
Группы предприятий (СБЕ) холдинга |
Номера СБЕ |
|
Первая: с критическим уровнем риска (4 СБЕ) |
1, 6, 15, 24 |
|
Вторая: с высоким уровнем риска (3 СБЕ) |
3, 4, 9 |
|
Третья: со средним уровнем риска (5 СБЕ) |
7, 10, 12, 20, 22 |
|
Четвёртая: с приемлемым уровнем риска (4 СБЕ) |
5, 16, 17, 23 |
|
Пятая: с низким уровнем риска (4 СБЕ) |
2, 18, 19, 21 |
Таблица 3
Итоговая группировка подразделений АО «УГМК» по уровню риска
|
Группы предприятий (СБЕ) холдинга |
Номера СБЕ |
|
Первая: с критическим уровнем риска (4 СБЕ) |
1, 6, 15, 24 |
|
Вторая: с высоким уровнем риска (3 СБЕ) |
3, 4, 9 |
|
Третья: со средним уровнем риска (5 СБЕ) |
7, 10, 12, 20, 22 |
|
Четвёртая: с приемлемым уровнем риска (4 СБЕ) |
5, 16, 17, 23 |
|
Пятая: с низким уровнем риска (4 СБЕ) |
2, 18, 19, 21 |
В табл. 2 приводятся результаты расчетов методом k-средних.
Применение дискриминантного анализа не позволило внести нетипичные объекты в кластеризацию.
Согласно критерию Хотеллинга была выявлена существенная различимость полученных кластеров.
После уточнения состава кластеров и подтверждения качества модели была получена итоговая группировка (табл. 3).
Первая группа характеризуется наихудшими значениями показателей устойчивости в трёх сферах деятельности предприятий холдинга, в то время как предприятия пятой группы являются наиболее устойчивыми (уровень риска минимален) (рис. 2).
Заключение
По результатам работы можно сделать вывод о том, что показатели ROA и ROAMM, как правило, растут при переходе от групп предприятий с наибольшим уровнем риска к группам с наименьшим. Так, ROA в первой группе составляет 0,06, а в четвертой – 0,15. Показатель Kа также коррелирует с уровнем риска.
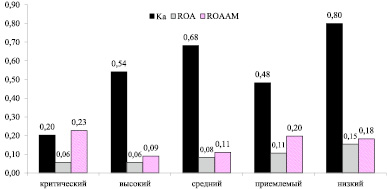
Рис. 2. График центров групп по уровням рисков рыночной деятельности
Таким образом, для формирования однородных по уровню риска рыночной деятельности групп предприятий холдинга целесообразно использовать метод k-средних при условии выделения пяти однородных по уровню риска групп предприятий – (критический, высокий, средний, приемлемый, низкий). Это разбиение является устойчивым по следующим причинам:
– прежде всего, применение в качестве первичных данных взвешенных значений используемых показателей рисков рыночной деятельности влечет к снижению случайных колебаний;
– реализация разнородных методов кластерного анализа позволила временно исключить подразделения холдинга, имеющие значительные отличия по показателям риска от основной массы предприятий, определить обоснованное число кластеров и получить наилучшее по выбранному критерию распределение подразделений по кластерам;
– возможность распределения ранее исключённых из выборки предприятий по уже выделенным кластерам позволяет существенно повысить качество классификации с учетом изменчивого финансово-экономического состояния подразделений холдинга.
По результатам проведенной работы устойчивость группировки была подтверждена. В случае потребности в актуализации используемых в расчетах данных необходимо пересчитывать показатели рисков рыночной деятельности с учетом новой информации. Однако повторная реализация использованного в работе инструментария не требуется. Тем не менее необходима проверка качества модели кластеризации.
Практические расчеты по предложенной модели кластеризации с векторным критерием, проведенные на примере вертикально-интегрированного холдинга АО «УГМК», подтвердили приведенные выводы.
Библиографическая ссылка
Максимов Д.А., Митрофанов Д.П. МЕТОДОЛОГИЯ КЛАСТЕРИЗАЦИИ ОБЪЕКТОВ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОЙ ПРИРОДЫ ПО УРОВНЮ РИСКА // Фундаментальные исследования. – 2019. – № 6. – С. 158-164;URL: https://fundamental-research.ru/ru/article/view?id=42503 (дата обращения: 25.04.2024).



