Из рассмотрения большого числа публикаций [1–8] в области производства фосфорсодержащих удобрений следует, что дальнейшее увеличение производства фосфорсодержащих удобрений требует вовлечения в переработку новых видов сырья. В этой связи наибольший интерес представляет более широкое использование для получения экстракционной фосфорной кислоты (ЭФК) бедных фосфоритных руд бассейна месторождения Каратау. С другой стороны, актуальным представляется поиск более эффективных энергосберегающих технологических решений, позволяющих получать более концентрированную фосфорную кислоту. Перспективной в этом отношении представляется дигидратно-полугидратная технология, реализация которой позволила бы получать непосредственно в технологическом процессе кислоту с концентрацией 32–34 % P2O5.
Сырье месторождения Каратау отличается относительно низким содержанием P2O5 (24–24,5 %) и высоким содержанием примесей (MgO, R2O3, SiO2 и др.). При разработке сырья такого качества существующими методами концентрация продукционной кислоты не превышает 20–21 %. Это приводит к большим энергозатратам при упаривании ЭФК для дальнейшей ее переработки. Кроме того, получается фосфогипс плохого качества, что не позволяет вести его дальнейшую переработку. В связи с этим возникают экологические проблемы.
Использование дигидратно-полугидратного (ДП) метода для руд бассейна Каратау позволило бы, с одной стороны, существенно повысить концентрацию продукционной фосфорной кислоты, а с другой стороны, снижение содержания P2O5 в фосфополугидрате также позволило бы осуществлять и его переработку.
Руда бассейна Каратау весьма трудно поддается обогащению. В необогащенном фосфатном сырье присутствует большое количество примесей, вредно влияющих на процесс экстракции (гораздо больше, чем в рудах других месторождений). Поэтому оптимальные режимы дигидратно-полугидратного процесса для Хибинского и Ковдорского апатитовых концентратов [2, 6] не могут дать эквивалентных результатов при использовании фосфатного сырья Каратау. В связи с этим целью экспериментальных исследований явилось изучение возможности получения крепкой (до 35 %) ЭФК из бедных фосфоритов Каратау и достаточно чистого α-полугидрата сульфата кальция (ПСК), используя двухстадийный метод без промежуточной фильтрации. Процессы сернокислотного разложения фосфатного сырья Каратау, кристаллизации дигидрата сульфата кальция (ДСК) и перекристаллизации его на второй стадии в ПСК весьма сложны, отсутствует достаточно обоснованное и однозначное представление об их механизме и движущих силах. Изучение этих вопросов могло бы способствовать построению математической модели, которая отражает основные физико-химические закономерности протекания процессов. С помощью математического моделирования возможно нахождение оптимальных условий проведения дигидратно-полугидратного процесса из фосфоритов Каратау.
Процесс перекристаллизации ДСК в ПСК происходит при температуре 85‒95 °С и описывается уравнением:
CaSO4·2H2O → CaSO4·0,5H2O + 1,5 H2O (1)
При построении математической модели полугидратной стадии воспользовались гипотезой, которая основана на экспериментальных данных [1], что процесс фазового перехода ДСК в ПСК в фосфорнокислых растворах идет главным образом через раствор, и рост кристаллов ПСК происходит в кинетической области. Другими словами, процесс перекристаллизации ДСК в ПСК происходит, главным образом, за счет разности растворимостей ДСК и ПСК, при этом происходит растворение ДСК, и из раствора растут кристаллы ПСК. Математическая модель полугидратной стадии включает в себя математическое описание процесса растворения ДСК, для этого вводим функцию распределения числа частиц ДСК по размерам и математическое описание процесса образования кристаллов ПСК из раствора, для чего вводим функцию распределения числа частиц ПСК по размерам.
Для описания процесса разложения кристаллов ДСК в ячейке идеального смешения периодического действия воспользовались следующей системой уравнений:
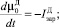 (2)
(2)
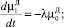 (3)
(3)
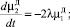 (4)
(4)
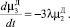 (5)
(5)
Для описания процессов образования и роста кристаллов ПСК в ячейке идеального смешения периодического действия используем систему уравнений:
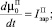 (6)
(6)
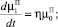 (7)
(7)
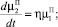 (8)
(8)
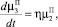 (9)
(9)
где 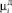 – i-й момент функции распределения ДСК (i = 0,…,3);
– i-й момент функции распределения ДСК (i = 0,…,3); 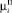 – i-й момент функции распределения числа частиц ПСК (i = 0,…,3); λД – скорость растворения ДСК; η – скорость образования ПСК;
– i-й момент функции распределения числа частиц ПСК (i = 0,…,3); λД – скорость растворения ДСК; η – скорость образования ПСК; 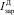 – скорость зародышеобразования ДСК;
– скорость зародышеобразования ДСК; 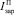 – скорость зародышеобразования ПСК.
– скорость зародышеобразования ПСК.
Рассматриваемая система характеризуется двумя независимыми движущими силами процесса растворения ДСК и двумя независимыми движущими силами процесса кристаллизации ПСК.
Считаем, что скорость зародышеобразования, роста и растворения кристаллов зависит главным образом от пересыщения раствора сульфатом кальция. Таким образом, для скоростей зародышеобразования можно записать следующие зависимости:
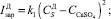 (10)
(10)
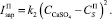 (11)
(11)
Скорость растворения дигидрата сульфата кальция представим в виде:
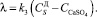 (12)
(12)
Скорость роста кристаллов полугидрата сульфата кальция можно записать следующим образом:
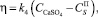 (13)
(13)
где k1, k2, k3, k4 – кинетические константы; 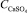 – концентрация сульфата кальция в растворе;
– концентрация сульфата кальция в растворе; 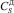 – равновесная концентрация дигидрата сульфата кальция в растворе;
– равновесная концентрация дигидрата сульфата кальция в растворе; 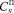 – равновесная концентрация полугидрата сульфата кальция в растворе.
– равновесная концентрация полугидрата сульфата кальция в растворе.
Тогда суммарную интенсивность растворения ДСК можно записать в виде:
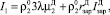 (14)
(14)
где 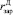 – радиус зародыша дигидрата сульфата кальция;
– радиус зародыша дигидрата сульфата кальция; 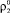 – плотность сульфата кальция.
– плотность сульфата кальция.
Суммарную интенсивность кристаллизации ПСК представим следующим образом:
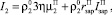 (15)
(15)
где 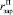 – объем зародыша полугидрата сульфата кальция.
– объем зародыша полугидрата сульфата кальция.
Уравнения (1)–(9) и соотношения (10)–(15) характеризуют качественно и количественно твердую фазу пульпы в зависимости от интенсивности протекающих в ней процессов.
Опишем жидкую фазу пульпы, для чего запишем баланс по компонентам жидкой фазы.
1. Уравнение изменения концентрации SO3 в растворе (масс. %):
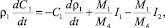 (16)
(16)
где ρ1 – плотность раствора; С1– концентрация SO3 в растворе (масс. %); М1 – молекулярная масса SO3; М4 – молекулярная масса CaSO4; I1, I2 – см. соотношения (14), (15).
Первый член в правой части уравнения (16) определяет изменение концентрации серной кислоты за счет изменения плотности раствора, второй член – за счет процесса растворения ДСК, последний член – за счет расхода серной кислоты на процесс кристаллизации ПСК.
2. Уравнение изменения концентрации P2O5 в растворе (масс. %):
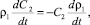 (17)
(17)
где С2 – концентрация P2O5 в растворе.
Концентрация P2O5 в растворе меняется только за счет изменения плотности раствора.
3. Уравнение изменения концентрации CaО в растворе (масс. %):
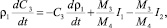 (18)
(18)
где С3 – концентрация CaО в растворе (масс. %); М3 – молекулярная масса CaО; М4 – молекулярная масса CaSO4.
В уравнении баланса CaО приход сульфата кальция в раствор определяется интенсивностью двух конкурирующих процессов: растворения ДСК I1 и кристаллизацией ПСК из раствора I2.
4. Уравнение изменения плотности раствора:
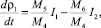 (19)
(19)
где М5 – молекулярная масса ДСК; М6 – молекулярная масса ПСК.
Плотность раствора меняется за счет разности в интенсивности процессов растворения ДСК, I1 и кристаллизацией ПСК из раствора I2.
Таким образом, математическая модель процесса представлена уравнениями (1)–(9) и (16)–(19) и соотношениями (10)–(15). Уравнения решаются методом конечных разностей. Неизвестными константами, определяемыми из сопоставления расчетных и экспериментальных данных, являются k1, k2, k3 и k4.
Скорость фазового перехода ДСК в ПСК в фосфорнокислых растворах определяется скоростями процессов растворения ДСК и кристаллизации ПСК из раствора. Неизвестными кинетическими константами, входящими в соотношения для скоростей основных процессов являются значения коэффициентов k1, k2, k3, k4. Варьируя значения этих констант, можно адаптировать математическую модель для определенного вида и качества сырья.
Кинетические параметры определяли из сопоставления расчетных и экспериментальных данных по значениям концентраций компонентов жидкой фазы и степени перекристаллизации ДСК в ПСК. Определение кинетических параметров осуществляли методом случайного поиска. Общая идея метода случайного поиска заключается в следующем. В процессе минимизации в окрестности точки yi определяется значение функции F(yi, …). Затем производится шаг в случайном направлении, определяемом случайным вектором αi. Величина шага задается параметром k. В результате этого находится новая точка yi + 1 = yi + kαi, в которой вычисляется значение функции Fi + 1. Если при выполнении случайного шага в направлении αi, приводящего в точку yi + 1, получается меньшее значение функции F (в случае минимума), то шаг считается удовлетворительным и новое значение Fi + 1 запоминается совместно с координатами точки yi + 1. После чего делается следующий шаг в случайном направлении αi + 1 и т.д. Если случайный шаг в направлении αi + 1 оказывается неудачным, то производится выборка следующего случайного вектора α и шаг выполняется снова из точки yi. Пробные шаги из точки yi делаются до тех пор, пока не будет найдена точка yi + 1, в которой функция F имеет значение меньше, чем в точке yi.
В качестве критерия рассогласования взяли соотношение
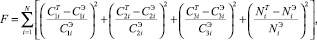 (20)
(20)
где Ck (k = 1, 2, 3) – концентрация компонентов раствора; N – степень перекристаллизации ДСК в ПСК; индексы T и Э обозначают теоретические данные, полученные в результате расчетов по математической модели и результаты экспериментальных исследований (см. главу II) соответственно.
Найденные с помощью метода случайного поиска значения кинетических констант для скоростей процесса растворения кристаллов ДСК равны:
k1 = 0,166·1025 (м–3·с–1);
k3 = 0,666·10–14 (м·с–1).
Значения кинетических констант для скоростей зародышеобразования и роста кристаллов ПСК приведены ниже
k2 = 0,833·1023 (м–3·с–1);
k4 = 0,999·10–14 (м·с–1).
Полученная математическая модель адекватно описывает процесс перекристаллизации ДСК в ПСК в условиях дигидратно-полугидратного процесса получения ЭФК.
Для проведения расчетов по второй стадии (по схеме без промежуточной фильтрации между стадиями) брали расчетные значения в конце первой стадии по концентрациям в растворе, плотности раствора, по первым трем моментам плотности функции распределения частиц дигидрата сульфата кальция по размерам, а также по среднему размеру дигидрата сульфата кальция. Эти значения являлись начальными данными при расчете второй стадии.
Из анализа расчетных и экспериментальных данных по стадии перекристаллизации ДСК в ПСК можно сделать следующие выводы:
– Проверена гипотеза о том, что фазовый переход ДСК в ПСК в фосфорнокислых растворах, содержащих MgO и другие примеси, происходит главным образом через жидкую фазу за счет разности растворимости ДСК и ПСК. При этом растворяется ДСК, а из раствора кристаллизуется ПСК.
– Выявлено, что увеличение концентрации P2O5 приводит к ухудшению процесса перекристаллизации. Поэтому непрерывный процесс следует вести при достаточно невысоких концентрациях P2O5 на второй стадии порядка 31–32 %.
– Определено, что чем выше начальная концентрация серной кислоты на первой и второй стадиях дигидратно-полугидратного процесса, тем выше степень перекристаллизации и больше размер кристаллов ПСК. Однако, так как коэффициент извлечения P2O5 в раствор хуже при высоких концентрациях SO3 на первой стадии, то непрерывный процесс следует вести при концентрации SO3 на дигидратной стадии порядка 1,6–2,0 %. Концентрацию SO3 на стадии перекристаллизации следует поддерживать в пределах 5–17 %.
– Выявлено влияние температуры на второй стадии на интенсивность фазового перехода ДСК в ПСК. Чем выше температура процесса, тем выше степень перекристаллизации. Непрерывный процесс необходимо вести при температуре порядка 95–97 °С.
Работа выполнена в рамках государственного контракта № 11.519.11.5005 с Министерством образования и науки РФ.
Рецензенты:
Бессарабов А.М., д.т.н., профессор, заведующий учебно-научным комплексом, ФГУП «Государственный научно-исследовательский институт химических реактивов и особо чистых химических веществ «ИРЕА», г. Москва;
Таран А.Л., д.т.н., .профессор кафедры «Процессы и аппараты химической технологии» имени Н.И. Гельперина Московского государственного университета тонких химических технологий имени М.В. Ломоносова, г. Москва.
Работа поступила в редакцию 18.03.2013.



