Одним из современных методов синтеза систем автоматического управления (САУ) является синтез интеллектуальных САУ [2] Особенность систем данного класса заключается в использовании нейросетевых структур и нечеткой логики для управления сложными динамическими объектами, способных функционировать в условиях неопределенности математического описания объекта управления. Под неопределенностью в данном случае понимается неопределенность, обусловленная как недостатком информации, необходимой для получения количественного описания протекающих в системе процессов, так и сложностью объекта управления. Применение классических методов синтеза, как правило, предполагает, что объекты управления описываются линейными динамическими звеньями невысокого (обычно не выше третьего) порядка. Указанное допущение часто приводит к тому, что классические регуляторы на практике не обеспечивают заданные показатели качества управления.
Интеллектуальные САУ, использующие аппарат искусственных нейронных сетей (ИНС) и нечеткую логику, позволяют проводить идентификацию сложных нелинейных динамических объектов и синтезировать для них нелинейные законы управления, что дает возможность решать рассматриваемую задачу синтеза САУ в условиях неопределенности на основе имеющихся экспериментальных данных, полученных на объекте. Применение ИНС в задачах синтеза САУ имеет существенный недостаток: информацию об объекте управления нейронная сеть получает в процессе обучения, а для этого необходим большой объем экспериментальных данных. Избежать данного недостатка возможно путем применения структур нечеткой логики, позволяющей обеспечить формализацию качественных, размытых в смысловом отношении, понятий и связей. На основе методов нечеткой логики удается проектировать САУ [1], способные эффективно функционировать в условиях наличия информации об объекте управления лишь качественного характера.
Нейро-нечеткие модели могут быть реализованы несколькими способами. В простейшем случае совместную модель [5, 7] можно рассматривать, как препроцессор, где механизм обучения искусственной нейронной сети (ANN) определяет правила нечеткого вывода (FIS). Как только параметры FIS определяются, ANN работает в обычном режиме (рис. 1). Функции принадлежности обычно аппроксимируются нейронной сетью из обучающих данных.
Другой подход в реализации нейро-нечетких моделей – это параллельная модель [5], которой нейронная сеть помогает нечёткой системе определить требующиеся параметры, особенно если входные переменные системы не могут быть непосредственно измерены. Обучение происходит только в нейронной сети, и нечёткая система остаётся неизменной. В некоторых случаях нечёткие выходы не могут быть непосредственно применены к процессу. В этом случае нейронная сеть может действовать как постпроцессор нечётких выходов. На рис. 2 представлена параллельная нейро-нечёткая модель, в которой входные данные подаются на нейронную сеть, а выход из нейронной сети дополнительно обрабатывается с помощью нечёткой системы.
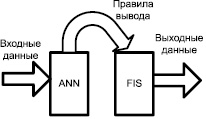
Рис. 1. Совместная нейро-нечеткая модель
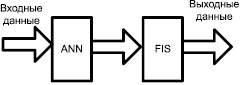
Рис. 2. Параллельная нейро-нечёткая модель
Наиболее распространенной являются интегрированные модели, в которых обучающий алгоритм нейронной сети используется для определения параметров системы нечёткого вывода. Нечёткая система вывода и соответствующие функции принадлежности базируются на априорных знаниях системы. С другой стороны, механизм обучения нейронной сети не зависит от априорной информации, а является стандартным для выбранной архитектуры искусственной нейронной сети.
Принцип функционирования нейро-нечеткой модели в задачах автоматического управления может быть иллюстрирован на примере наиболее распространённой модели ANFIS (Adaptive-Network-Based Fuzzy Inference System) [3]. ANFIS – адаптивная сеть нечеткого вывода реализует нечёткую систему Такаги – Сугено и представляет собой пятислойную нейронную сеть прямого распространения сигнала (рис. 3).
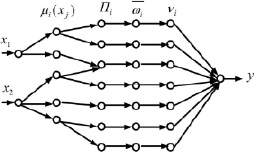
Рис. 3. Структура ANFIS-сети
Входные переменные модели x1 и x2 – управляемые переменные (на практике чаще всего применяется рассогласование между заданным и текущим значением управляемой переменной), выходные переменные y – управляющее воздействие.
Первый слой определяет нечеткие термы входных параметров. Выходы узлов этого слоя представляют собой значения функции принадлежности при конкретных значениях входов μi(xj).
Второй слой определяет посылки нечетких правил. Данный слой – неадаптивный. Каждый узел этого слоя соответствует одному нечеткому правилу. Узел второго слоя соединен с теми узлами первого слоя, которые формируют предпосылки соответствующего правила. Выходами узла ωi является степень выполнения правила, которая рассчитывается как произведение входных сигналов.
Третий слой осуществляет нормализацию степеней выполнения правил
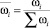 .
.
Неадаптивные узлы этого слоя рассчитывают относительный вес выполнения нечеткого правила.
Четвертый слой определяет вклад каждого нечеткого правила в выход сети. Узел четвертого слоя рассчитывает вклад нечеткого правила vi в выход сети.
Пятый слой формирует управляющий сигнал

Выбор нейро-нечетких моделей осуществляется в зависимости от класса решаемых задач. Так, для интеллектуального управления наибольшее применение получили модели ANFIS, FALCON, GARIC, NEFCON, FUN.
Рассмотрим особенности каждой из моделей.
ANFIS (Adaptive-Network-Based Fuzzy Inference System) – адаптивная сеть нечеткого вывода реализует нечёткую систему Такаги – Сугено и представляет собой пятислойную нейронную сеть прямого распространения сигнала.
Структура ANFIS гарантирует, что каждый лингвистический термин представлен только одним нечётким множеством. Процедура обучения из ANFIS не имеет ограничений на модификацию функций принадлежности. Из-за высокой гибкости адаптивных сетей ANFIS может иметь множество вариантов исполнения и реализации алгоритмов адаптивного управления в системах автоматического управления.
Модель FALCON (Fuzzy Adaptive learning Control Network) [8] имеет пятислойную архитектуру и реализует тип нечёткого вывода Мамдани (рис. 4). Структура приведена для объекта управления с двумя входными и одним выходным сигналом.
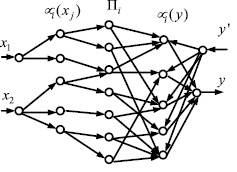
Рис. 4. Структура FALCON-сети
Первый скрытый слой отвечает за фаззификацию каждой входной переменной. Второй скрытый слой определяет предпосылки правила с последующим следствием из правил в третьем скрытом слое. FALCON использует двухэтапный алгоритм, состоящий из обучения без учителя и параметрической оптимизации на основе метода градиентного спуска. На первом этапе параметры функции принадлежности определяются самоорганизующимися методами обучения аналогично статистическим методам кластеризации. После того определяются правила-предпосылки. После определения нечеткой базы правил устанавливается вся структура сети. Второй этап обучения осуществляет настройку параметров входа и выхода оптимальных функций принадлежности. Алгоритм обратного распространения используется для обучения с учителем. Такие свойства модели FALCON делают ее особо ценной для задачи параметрической идентификации в адаптивных САУ с настраиваемой моделью.
GARIC (Generalized Approximate Reasoning based Intelligent Control) является пятислойной сетью. GARIC использует минимаксный метод для вычисления выходных правил. Для этого метода необходимо чёткое выходное значение из каждого правила. Следовательно, выводы должны быть дефаззифицированы, прежде чем они накопятся в конечное выходное значение контроллера. GARIC в качестве алгоритма обучения использует метод градиентного спуска и обучения с учителем. Обучение останавливается, если выходной сигнал сети прекращает изменяться. Относительно сложная процедура обучения и архитектура являются основными недостатками GARIC, но несмотря на это модель GARIC обеспечивает наилучшие показатели качества в системах автоматического управления.
Алгоритм обучения для NEFCON (Neuro-Fuzzy Control) [5, 6] способен распознавать нечёткие множества, а также нечёткие правила реализации типа систем нечёткого вывода Мамдани [4, 5]. Особенностью NEFCON является то, что связи взвешиваются с нечёткими множествами вместо действительных чисел. NEFCON использует инкрементный или декрементный алгоритм обучения базы правил и алгоритм обратного распространения для обучения нечётких множеств. Система NEFCON способна встраивать ранние знания, а также обучаться с нуля, что делает ее особенно ценной в задачах синтеза с объектом «черный ящик». Производительность системы очень сильно зависит от эвристических факторов, таких как скорость обучения, меры ошибки и т.д.
FUN (Fuzzy Net) состоит из входа, выхода и трёх скрытых слоёв. Настройка FUN начинается с фиксированного количества правил и фиксированного количества нечетких множеств для каждой переменной. Далее используется стохастическая процедура, которая изменяет параметры функций принадлежности и связи в структуре сети. Процесс обучения приводится в действие функцией изменения, которая вычисляется после случайной модификации. FUN может обучаться по стандартным нейронным стратегиям обучаемых сетей или обучаться с учителем. Основная особенность модели FUN состоит в том, что алгоритм перестройки связей и изменения параметров функций принадлежности носит случайный характер. Это означает, что и производительность модели будет носить случайный характер. Поэтому данная модель не может быть применена в системах управления реального времени.
Анализ существующих нейро-нечетких моделей показал, что выбор типа модели зависит от многих факторов. В качестве ориентира используются для повышения «интеллекта»: быстрота обучения, онлайн адаптивность, достижение глобального уровня ошибок и недорогие вычисления. Как правило в качестве нечетких моделей выбираются модели Мамдани или Сугено. Нечёткие системы типа Сугено являются высокопроизводительными, но часто требуют сложных процедур обучения. Нечёткие системы типа Мамдани используют более быстрые эвристические методы, но с потерей в производительности. Многие нейро-нечёткие модели используют контролируемые и неконтролируемые методы для распознавания различных параметров системы вывода. Проблемным является процесс обучения, который не гарантирует оптимальность в глобальном смысле. Исследования показывают, что техника градиента спуска находит локальный оптимум. Применение глобальных процедур оптимизации позволяет предотвратить «попадания в ловушку» локального оптимума, но увеличивает трудоемкость алгоритма.
Таким образом, применение нейро-нечетких моделей в задачах синтеза систем автоматического управления наряду с явными достоинствами оставляет не полностью решенными многие проблемы, связанные с методологией анализа и синтеза рассматриваемых систем.
Рецензенты:
Бочкарев С.В., д.т.н., доцент, профессор кафедры «Микропроцессорные средства автоматизации», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Южаков А.А., д.т.н., профессор, заведующий кафедрой «Автоматика и телемеханика», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Работа поступила в редакцию 06.11.2014.



