Повышение физико-химической активности среды приводит к увеличению активной поверхности твердых компонентов вяжущих и к повышению реакционноспособности и активации процесса гидратации вяжущих и бетонов.
Улучшение эксплуатационных свойств бетонов и снижение энергозатрат на их получение может быть достигнуто путем предварительной механохимической обработки цементной и вяжущей композиции в сухом виде, в различных мельницах, и в жидкой среде – в роторно-пульсационных аппаратах с одновременным использованием различных минеральных наполнителей и добавок модификаторов [1, 2, 3, 4, 5].
Известно, что для увеличения скорости химических реакций необходима энергетическая активация реагирующей системы [6]. Требуемая величина активации Е при заданных значениях константы скорости реакции Кт и температуре Т процесса определяется по уравнению Аррениуса:
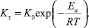
Энергия активации Еа при этом направлена на перевод веществ и всей реагирующей системы в термодинамически неустойчивое состояние и может быть в виде тепловой, радиационной, импульсной и др. Отсюда реагирующим системам, которые уже имеют высокий исходный энергетический уровень, требуются меньшие энергетические затраты, и наоборот. Величина уменьшения энергозатрат равна величине повышения исходного энергетического уровня веществ реагирующей системы. Это положение основано на первом начале термодинамики – законе сохранения энергии и является основой системного подхода к прогнозированию энергозатрат синтеза искусственного камня. Классическое условие прохождения реакции взаимодействия веществ:
А + В → С + Q↑,
где А – активное вещество системы (при Т = 298°К); В – инертное вещество системы (при Т = 298°К); С – требуемый продукт реакции; Q – тепловой эффект реакции, который определяет необходимость перевода в неустойчивое возбужденное состояние инертного вещества В системы при недостаточности самостоятельной активности вещества А всего процесса реакции с определенной скоростью при данной температуре (298 К). Если вещество В не перевести в термодинамически неустойчивое состояние тепловой, радиационной, механомеханической, импульсной и др. обработкой, то реакция будет протекать медленно или практически будет отсутствовать.
Подведенная к реагирующей системе энергия активация Еа будет направлена, прежде всего, на повышение энергетического состояния вещества В до реакционноспособного уровня Ур, иначе для преодоления энергетического «барьера» протекания реакции взаимодействия веществ А и В. Значение уровня Ур будет ниже, чем выше, при равных условиях реакции (химическая активность веществ А, концентрация и др.), исходное энергетическое состояние инертных веществ Вi. Разница между ними равна разнице энергий активации процессов:
Eb1 – Eb2 = Eа1 – Eа2 = ΔЕ,
где Еb1 – внутренняя энергия веществ, определение его в реальности невозможно; ΔЕ – показатель, характеризующий энергетическое отличие инертных веществ.
В настоящее время проводится комплекс исследований в направлении изучения параметров электромагнитной активации и механизма направленной активации воды затворения, констант скорости реакции и определения совокупного энергетического эффекта.
Возвращаясь к вышесказанному, хочется акцентировать, что здесь вопрос стоит об эффективности подачи энергии активации в реагирующую систему, т.к. в известных работах не приведен анализ эффективности подачи энергии извне [3, 4, 5].
Например, тепловой подвод энергии не всегда эффективен, т.к. в реагирующих системах твердые компоненты многофазны и адресный подвод для разрушения связей отсутствует, иначе говоря, к системе подводится единая частота и амплитуда колебаний от тепловой энергии, тогда как в твердом компоненте системы существует определенный набор связей молекул, супермолекул, кластеров с определенными колебательными параметрами, и отсюда требуется избирательный адресный подвод энергии, например в виде электромагнитных колебаний с набором соответствующих частот и амплитуд по времени и продолжительности, которые должны вызвать ответные резонансные колебания в твердом компоненте и отсюда ускорить процессы диссоциации с последующим ускоренным взаимодействием компонентов в реагирующей системе.
Для рассмотрения вопросов, связанных с процессами диссипации в качестве исходной предпосылки воспользуемся равновесием диссоциации некоторого электролита (воды) в произвольном растворителе:
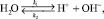(1)
где k1 и k2 – константы скоростей; H+ и OH– – сольватированные катион и анион. С точностью до гидродинамических флуктуаций сдвиг равновесия вправо увеличивает локальную плотность зарядов, влево – уменьшает. При фиксированной концентрации вещества средняя длина свободного пробега ионов H+ и OH– конечна. Согласно общим положениям механики, любое одномерное конечное движение есть колебательное, имеющее предельные циклы с асимптотической устойчивостью. Для раскрытия физического содержания этих колебаний представляется оправданным сделать кинетический анализ равновесия диссоциации (1) произвольного электролита.
Система уравнений, характеризующая процесс равновесия (1), выглядит следующим образом:
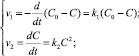(2)
(3)
здесь С0 – начальная концентрация электролита; С – концентрация диссоциированных молекул электролита. Очевидно, что С0 – С = d есть концентрация недиссоциированных молекул.
Данная система уравнений предполагает два различных варианта анализа для сильных и слабых электролитов. Главными критериями этого являются следующие условия:
1) для сильных электролитов С0 >> d;
2) для слабых электролитов (вода, другие растворители и их растворы) d >> С.
Приведенная система уравнений соответствует общим положениям понятия химического равновесия. Так, при v1 = v2 (2), (3) получаем константу равновесия
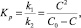
соответствующую закону разбавления Оствальда. При этом структура уравнения (1) предполагает использование критерия устойчивости по Ляпунову. Согласно данному критерию, некоторая произвольная функция v(y) непрерывно дифференцируема и для которой выполняются следующие условия:
v(y) > 0 при y 1 0, v(0) = 0 при y = 0
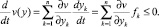(4)
Для исследуемой системы уравнений параметр y соответствует концентрации С. При кинетическом анализе равновесия диссоциации некоторого электролита представляется интересным второй вариант последнего условия (4), когда возможны асимптотические устойчивости и вероятны предельные циклы на фазовой плоскости. Таким образом, нам необходимо показать, что система уравнений (2), (3) имеет асимптотическую устойчивость (4), приводящую к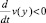 
.
Данное требование предполагает исследование условия критерия устойчивости по Ляпунову (4) для производной по времени от скорости v1 в представлении (3), обеспечивающем генерацию ионов, определяющих все параметры:
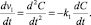(5)
Поскольку скорости v1 и v2 в (2), (3) являются сопряженными величинами, то в последнем выражении вместо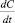 
можно взять его значение для v2 из (3). Тогда
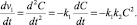
Так как C = C0 – d, возможно следующее представление выражения (5):
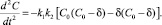
Поскольку для сильных электролитов, как это отмечено ранее, C0 >> d, можно пренебречь вторым слагаемым в правой части. Тогда при C = C0 – d имеет место
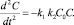
А это есть уравнение гармонических колебаний с решением:
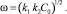(6)
По существу, данный результат является частотой популяционных колебаний Лотки - Вольтерры [7].
Сопоставление данного результата требует определения в (6) значения констант скоростей k1 и k2:
k1 = 2,6•10–5 с–1 ;
k2 = 1,3•1011 л•моль/с;
с = 55,54 моль/л [8].
Отсюда
ω = (2,6•10–5•1,3•1011•55,54) = 13,7 кГц.
Решение этой задачи возможно по второму варианту анализа устойчивого состояния процесса (1), предполагает исследование производной по времени скорости обратного процесса (диссоциации молекул воды V2 (3). Из уравнения (3) следует
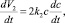(7)
где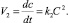 
Тогда
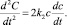(8)
Поскольку скорости V1 и V2 являются сопряженными (взаимозависимыми), подставляем в (2) вместо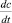 
ее значение из скорости V1 в виде
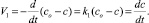
В этом случае имеет место
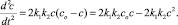
Для слабых электролитов, каковым является и вода, имеет место Со >> С (при со = 55,54 моль/л
С = [Н+ ] = [ОН– ] = 10–7 моль/л).
Формально можно линеаризовать (7) по первому члену. Тогда
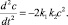
Но концентрация диссоциированных молекул воды С, как это показано выше, равна С = Со – δ, где δ – концентрация недиссоциированных молекул воды. При этом δ ≅ Со. Тогда
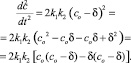(9)
Поскольку Со ≈ δ, то можно пренебречь первым слагаемым в (9). В этом случае
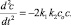(10)
Так как (10) имеет колебательный характер, то имеет место операторное тождество:
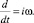
Отсюда следует
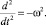
Это дает основание следующему представлению:
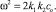(11)
Подставляя сюда значения k1 и k2, а также со = 55,54 моль/л, [8] получаем
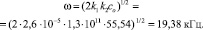
Из результатов (6) и (11) большей потенциальной энергии (большей потенциальной яме) соответствует частота 19,38 кГц, и тогда эволюция системы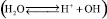 
идет по частоте 19,38 кГц, что согласуется с данными М.А. Маргулиса [8] .
Таким образом, результат, полученный на основании кинетического анализа процесса равновесия, свидетельствует, что сольватированные ионы, совершающие колебательные движения, дают возможность использования силы вязкости для получения уравнения электропроводности через подвижность b, и повышение физико-химической активности среды гидратации является фактором снижения энергетических затрат на процесс ускоренного твердения вяжущих веществ и бетонов. Электромагнитная активация приводит к увеличению прочности бетонов на 40–50 % в возрасте 3 сут, а в 28 сут – на 25–30 %, и активированные бетоны характеризуются высокими эксплуатационными показателями.
Регулирование процесса гидратации вяжущих воздействием электромагнитной активации происходит за счет образования активных форм воды (радикалов). Воздействие этих радикалов при смешивании вяжущего с водой способствует увеличению удельной поверхности вяжущих или уменьшению их размеров. Образование парогазовых пузырьков воды, т.е. возникновение кавитации в порах зерен вяжущего, происходит за счет резонансного поглощения энергии электромагнитного поля с собственными частотами воды f ≈ 20 кГц, при этом в порах растет объем воды и происходит схлопывание кавитационных пузырьков и разрыв межмолекулярных (водородных, Ван-дер-ваальсовых) связей зерен вяжущих веществ, что приводит к увеличению удельной поверхности их и ускорению реакции гидратации. Далее диспергация частиц зерен вяжущих веществ происходит за счет воздействия активных форм молекул воды (радикалов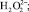 
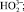OH– ), образующихся при резонансном поглощении водой электромагнитных колебаний в области частот 13–20 кГц, определяемых соотношениям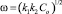и
и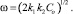 
Механизм разложения (расщепления) воды на свободные радикалы заключается в кинетике диссоциации молекул воды. В скрытый или индукционный период также оказывается воздействие электромагнитной активации, когда образуется гелевая оболочка, ускорение диффузии приводит к разрушению гелевых оболочек и ускорению гидратации.
Выводы
Воздействие электромагнитной активации приводит к термодиффузии и снижению энергетических затрат. Целенаправленное регулирование диффузионных процессов при воздействии электромагнитной активации приводит к упорядочению столкновений супермолекул (кластеров), число которых остается прежним, если температура не изменилась, и число которых увеличивается с повышением температуры, отсюда ускорение диффузии и, соответственно, гидратации вяжущих и бетонов.